工程上,钢材的剪切强度一般取为拉伸强度的0.58倍,即 \tau =0.58\sigma 。
在Ferdinand P.Beer等人著作的《MECHANICS OF MATERIALS》中:
0.58是钢材在纯剪切情况下,根据第四强度理论计算得来。
这里有俩概念:
一是纯剪切状态,根据《材料力学》的描述,纯剪切本质上是拉-压二向应力状态;
二是第四强度理论。
推导过程中将涉及应变能、应变能密度、韧性模量、回弹模量、畸变能等听起来复杂实则非常易于理解的概念。
应变能
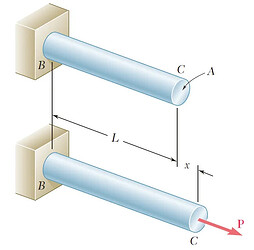
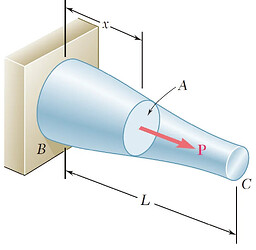
图1 拉力P对杆件做功
正如图1里看到的,杆件在单轴受拉情况下,作用力P导致其产生微小的位移dx。所做的功(单位J-焦耳,1焦耳=1N·m)为:
dU=Pdx (1)
积分形式:
U=\int_{0}^{x_{1} } Pdx (2)
也就是说,拉力P作用下导致拉杆发生变形所做的总功为图2力-位移曲线中x1段的面积。P做的功导致了与杆件变形相关的能量的增加,这种能量U被称为杆件的“应变能”。
在线弹性受力情况下,力和位移呈线性正相关,所以根据公式(2)可以得到应变能和力 P=kx (k为直线斜率)以及位移x的函数关系式:
U=\int_{0}^{x_{1} } Pdx=\int_{0}^{x_{1} } kxdx=\frac{1}{2} kx_{1}^{ 2} (3)
应变能密度
在P作用下,对于均质材料其单位体积所产生的应变能为:
\frac{U}{V} =\int_{0}^{x} \frac{P}{A} \frac{dx}{L} (4)
根据胡克定律,P/A为截面应力 \sigma _{x} ;x/L为正应变 \varepsilon _{x} 。所以进一步得到:
u=\frac{U}{V} =\int_{0}^{\varepsilon }\sigma _{x} d\varepsilon _{x} (5)
应变能与杆件体积的比值被称为“应变能密度”,用u表示。
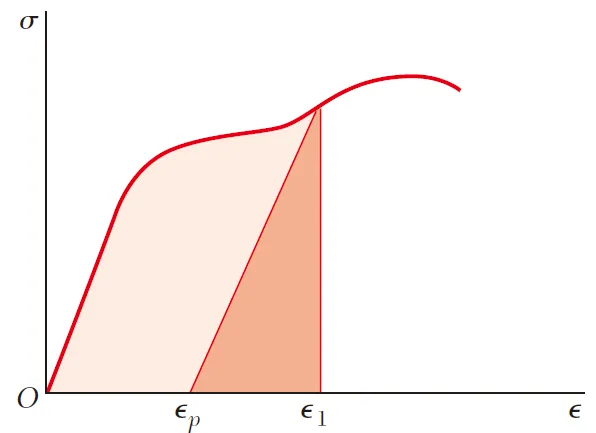
图3
图3意思是:当拉力P导致杆件发生塑性变形时,即应变从0发展到 \varepsilon _{1} ,此时撤消拉力P,杆件截面应力回归到0,与此同时杆件会发生一定回弹,最终应变是 \varepsilon _{p} ,应变的回弹量为 \varepsilon _{1} -\varepsilon _{p} 。
图3中深色区域的面积即为恢复的应变能密度,而浅色区域的面积与杆件体积相乘,就是拉伸过程中产生并耗散掉的热量。
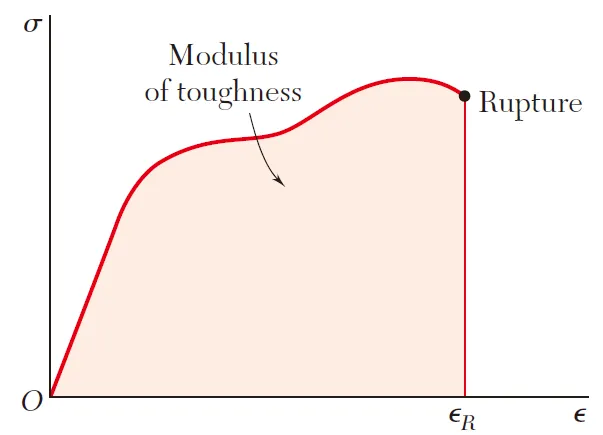
图4
把材料断裂时的极限应变带入公式(5)得到的数值,就被叫做材料的“韧性模量”,其数值等于图4中全部的浅色区域面积,含义是“为使材料发生断裂所需要的应变能密度”。
但是如果截面应力位于弹性极限以内,即图4中的直线段,根据胡克定律:
\sigma _{x} =E\varepsilon _{x} (6)
将(6)带入公式(5):
u=\frac{U}{V} =\int_{0}^{\varepsilon _{1} } E\varepsilon _{x} d\varepsilon _{x} =\frac{E\varepsilon _{1}^{2} }{2} =\frac{\sigma _{1}^{2} }{2E} (7)
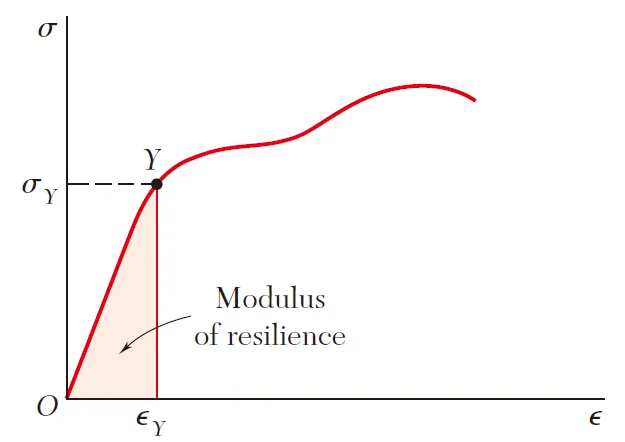
图5
把屈服强度 σ_Y 带入公式(7),得到的应变能密度(图5浅色区域面积)又被称作材料的“回弹模数”,即:
u_{Y} =\frac{\sigma _{Y}^{2} }{2E} (8)
了解上述基本概念之后,咱们再看看3种 不同应力状态下的应变能U&应变能密度u。
正应力下的弹性应变能
图6
前面讲应变能密度的时候,举的例子是等截面杆件,应力的分布很均匀。但是对于图6中的变截面构件来说,其横截面应力分布并不均匀。对于这种情况,可截取一小段体积ΔV计算应变能密度:
u=\frac{dU}{dV} (9)
当线弹性阶段内某一点应力为 \sigma _{x} ,应变为 \varepsilon _{x} ,根据公式(8)同理可得该点应变能密度:
u=\frac{\sigma _{x} ^{2} }{2E} =\frac{1}{2} \sigma _{x} \varepsilon _{x} (10)
那么根据公式(9),在单轴拉伸正应力作用下的ΔV这一小段的弹性应变能为:
dU=udV (11)
或
U=\int \frac{\sigma _{x} ^{2} }{2E} dV (12)
在拉力P作用下,距离端部x处的横截面为A的截面应力为 \sigma _{x} =P/A ,代入公式(12)得到:
U=\int \frac{P ^{2} }{2EA^{2} } dV (13)
其中dV是不规则微小段ΔV的体积,当它的长度足够小时,可以近似认为 dV=Adx ,再次代入公式(13)得应变能与微小段长度dx的函数关系表达式为:
U=\int_{0}^{L} \frac{P^{2} }{2EA} dx (14)
当构件为等截面杆件时,A为定值,可以很容易根据公式(14)求出P作用下的应变能:
U=\frac{P^{2} L}{2EA} (15)
剪切应力下的弹性应变能
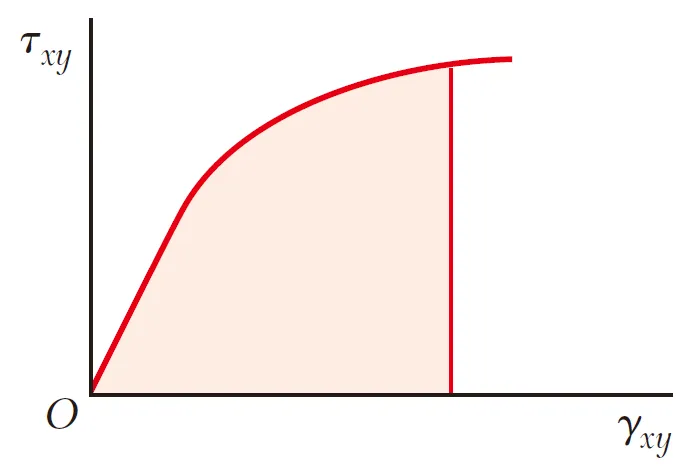
图7
当材料受到剪应力τxy时,结合图7剪应力-应变图和公式(5)同理可得应变能密度为:
u=\int_{0}^{Y_{xy} } \tau _{xy} d\gamma _{xy} (16)
应变能密度即为图7中浅色区域面积。
在线弹性阶段,剪切应力 \tau _{xy} =G\gamma _{xy} ,G为剪切弹性模量(或刚性模量)。将其代入公式(16)并求积分得:
u=\frac{1}{2} G\gamma ^{2} _{xy} =\frac{\tau _{xy}^{ 2} }{2G} =\frac{1}{2} \tau _{xy} \gamma _{xy} (17)
根据公式(9)和公式(12),同理可得剪切应力作用下弹性应变能:
U=\int \frac{\tau _{xy} ^{2} }{2G} dV (18)
复杂应力状态下的应变能
前面介绍了正应力状态下和剪切应力状态下的弹性应变能。
实际上,几乎所有构件在工作时,都处于复杂应力状态,包括:正应力 \sigma _{x} 、\sigma _{y} 、\sigma _{z} 和切应力 \tau _{xy} 、\tau _{yz} 、\tau _{zx} 。
复杂应力状态下的应变能密度可通过公式(10)和(17)求得:
u=\frac{1}{2} (\sigma _{x} \varepsilon _{x} +\sigma _{y} \varepsilon _{y} +\sigma _{z} \varepsilon _{z}+\tau _{xy} \gamma _{xy }+\tau _{yz} \gamma _{yz }+\tau _{zx} \gamma _{zx} ) (19)
把胡克定律 \varepsilon _{x} =\sigma _{x} /E 、\gamma _{xy} =\tau _{xy} /G 以及三向应力状态下单向应力对其它两个方向应变的影响(这样理解‘泊松比’的概念)代入公式(19)可得:
\begin{aligned} u = & \frac{1}{2E} [ \sigma_{x}^2 + \sigma_{y}^2 + \sigma_{z}^2 -2v(\sigma_{x}\sigma_{y} + \sigma_{y}\sigma_{z} + \sigma_{z}\sigma_{x}) ] \\ & + \frac{1}{2G}(\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2) \end{aligned} (20)
假设某一点坐标为(a,b,c),在三轴拉应力作用下,剪应力为0,那么就有:
u=\frac{1}{2E} \left [ \sigma _{a} ^{2} +\sigma _{b} ^{2}+\sigma _{c} ^{2}-2 v\left ( \sigma _{a} \sigma _{b } +\sigma _{b} \sigma _{c } +\sigma _{c} \sigma _{a} \right ) \right ] (21)
说到这里,需要提醒大家的是,单位长度的立方体在三向应力作用下,不仅体积发生变化而且形状也会发生变化(畸形)。那么复杂应力状态下的应变能密度u就被分成了两部分:体积改变能密度 u_{v} 和畸变能密度 u_{d} :
u=u_{v} +u_{d} (22)
我们知道,单位体积的改变只与三个主应力之和 \sigma _{a} +\sigma _{b} +\sigma _{c} 有关,三个主应力各自分摊的比例如何并不重要。
也就是说,用三个主应力平均值 (\sigma _{a} +\sigma _{b} +\sigma _{c} )/3 代替 \sigma _{a} 、\sigma _{b} 、\sigma _{c} ,单位体积的改变与 \sigma _{a}、\sigma _{b} 、\sigma _{c} 共同作用的情况一样。我们在这里可以引入平均应力:
\bar{\sigma } =\frac{\sigma _{a}+\sigma _{b} +\sigma _{c}}{3} (23)
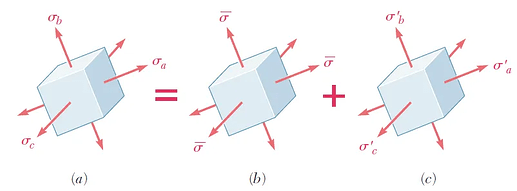
图8
如图8所示,可设:
\sigma _{a} =\bar{\sigma } +\sigma _{a} ^{'} (24)
\sigma _{b} =\bar{\sigma } +\sigma _{b} ^{'} (25)
\sigma _{c} =\bar{\sigma } +\sigma _{c} ^{'} (26)
\sigma _{a} ^{'} 、\sigma _{b} ^{'} 、\sigma _{c} ^{'} 分别是 \sigma _{a} 、\sigma _{b} 、\sigma _{c} 与平均应力的差值,且差值之和为0:
\sigma _{a}^{ '} +\sigma _{b}^{ '}+\sigma _{c}^{ '}=0 (27)
这就意味着三个差值有正有负,既有拉力也有压力,这样必然会导致单位体积产生变形(畸变)而体积不变(因为应力之和为0)。
说到这里,再想想图8提到的(a)状态下的应变能密度u分为体积改变能密度 u_{v} 和畸变能密度 u_{d} ,不难推断出两种能密度分别对应于(b)和(c)。
这下可以根据公式(21),把 \sigma _{a} 、 \sigma _{b} 、 \sigma _{c} 替换成平均应力代入,求得体积改变能密度 u_{v} :
u_{v} =\frac{1}{2E} \left [ 3\bar{\sigma} ^{ 2} -2v\left ( 3\bar{\sigma ^{2} } \right ) \right ] =\frac{3\left ( 1-2v \right ) }{2E} \bar{\sigma} ^{ 2} (28)
或代入公式(23)得:
U_{v} =\frac{1-2v}{6E} (\sigma _{a} +\sigma _{b} +\sigma _{c} )^2 (29)
联系公式(22),可得畸变能密度:
U_{d} =u-u_{v} =\frac{1+v}{6E} \left [ \left ( \sigma _{a} ^{2} -2\sigma _{a} \sigma _{b }+\sigma _{b} ^{2} \right ) +\left ( \sigma _{b} ^{2} -2\sigma _{b} \sigma _{c }+\sigma _{c} ^{2} \right ) +\left ( \sigma _{c} ^{2} -2\sigma _{c} \sigma _{a }+\sigma _{a} ^{2} \right ) \right ]
再根据弹性模量和剪切模量的关系:
E=2\left ( 1+v \right ) G
代入以上公式得:
u_{d} =\frac{1}{12G} \left [{ \left ( \sigma _{a} -\sigma _{b } \right ) ^{2} + \left ( \sigma _{b} -\sigma _{c} \right ) ^{2} + \left ( \sigma _{c} -\sigma _{a } \right ) ^{2} } \right ] (30)
对于单轴受拉杆件来说,如这样理解‘泊松比’的概念开头所说,y、z方向应力为0,所以 \sigma _{b} =\sigma _{c} =0,那么公式(30)就有:
u_{d} =\frac{\sigma _{a} ^{2} }{6G} (31)
当 \sigma _{a} 达到材料屈服强度 \sigma _{Y} 时,有畸变能密度:
\left ( u_{d} \right ) _{Y} =\frac{\sigma _{Y} ^{2} }{6G}
如果公式(30)计算数值小于公式(31)的计算数值,就可以认为材料不会发生屈服:
\left ( \sigma _{a} -\sigma _{b} \right ) ^{2} +\left ( \sigma _{b} -\sigma _{c} \right ) ^{2}+\left ( \sigma _{c} -\sigma _{a} \right ) ^{2}< 2\sigma _{\gamma} ^{2} (32)
这就是最大畸变能理论,也被称为第四强度理论。
一开头咱就说纯剪切本质上是拉-压二向应力状态,\sigma _{a} =\tau ,\sigma _{b} =0 ,\sigma _{c} =-\tau
代入公式(32)有:
\tau ^{2} +\tau ^{2} +\left ( -\tau -\tau \right )^{ 2} < 2\sigma _{\gamma} ^{2}
\tau < \frac{\sigma _{Y} }{\sqrt{3} } \approx 0.58\sigma _{_{Y} } (33)
公式(33)是材料在纯剪切情况下不发生屈服的条件,换句话说 0.58\sigma _{_{Y} } 就是材料发生屈服的临界点。