泊松比是结构设计中常常用到的参数,百科对泊松比的解释为:
泊松比是指材料在单向受拉或受压时,横向正应变与轴向正应变的比值,也叫横向变形系数,它是反映材料横向变形的弹性常数。
一般来说标准中都会给出不同材质的泊松比取值,直接采用即可。本文抽丝剥茧,从源头搞清楚泊松比含义及其影响。
2种应力状态
单向应力状态
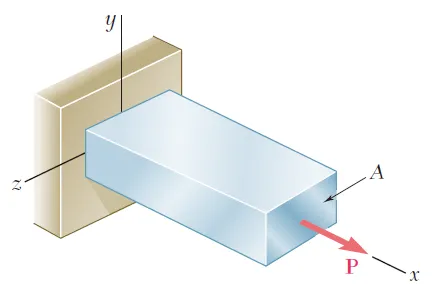
当由各向同性且均质的材料制成的杆件横截面积为A,在受到轴向拉力P作用时,其横截面应力 \sigma _{x} =\frac{P}{A} 。
图1
当该应力不超过材料的弹性极限时,根据胡克定律,其应变
\varepsilon _{x} =\frac{\sigma _{x} }{E} (1)
其中,E为材料弹性模量。
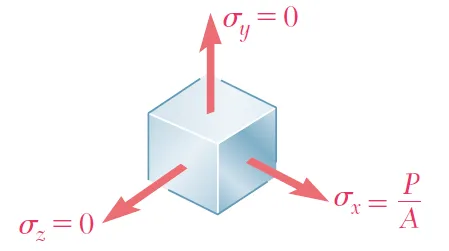
我们可以很清楚地知道,杆件所受拉力P沿x轴方向,那么垂直于x轴的y、z方向的应力必为0:\sigma _{y} =\sigma_{ z} =0 ,如图1所示。根据上面提到的公式(1),当y、z方向的应力为0时,相应的应变也应该为0:\varepsilon _{y} =\varepsilon _{z} =0 。
图2
可遗憾的是,事实并非如此。
所有的各向同性且均质的材料,受到一个方向(例如x方向)的轴向拉力时,该方向伸长的同时往往伴随着其它方向(如y、z方向)的缩小,且对其它方向(如y、z方向)造成的应变数值相同,即 \varepsilon _{y} =\varepsilon _{z} ,我们管它们叫做“横向应变”。
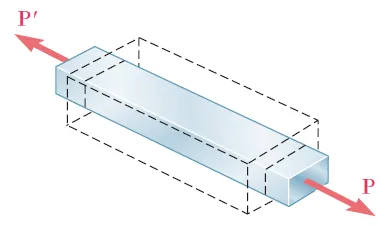
图3
这一现象首先被法国数学家西莫恩·德尼·泊松发现,由此他提出了一个新的概念——泊松比:
u=-\frac{侧应变}{轴向应变} (2)
或者
v=-\frac{\varepsilon _{y} }{\varepsilon _{x} } =-\frac{\varepsilon _{z} }{\varepsilon _{x} } (3)
公式中的负号“-”代表轴向应变与侧应变方向相反。
将公式(3)带入到公式(1),我们就会得到轴向拉力P作用下,y、z两个方向上的应变:
\varepsilon y=\varepsilon z=-\frac{v\sigma _{x} }{E} (4)
上面说的是单向应力状态下的泊松比给应变带来的影响,譬如上面提到的 \sigma _{x} =\frac{P}{A} 且 \varepsilon _{y} =\varepsilon _{z} =0 的情况。
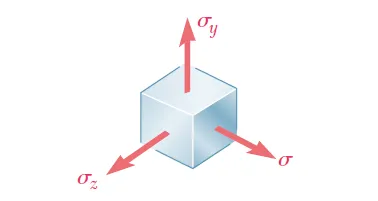
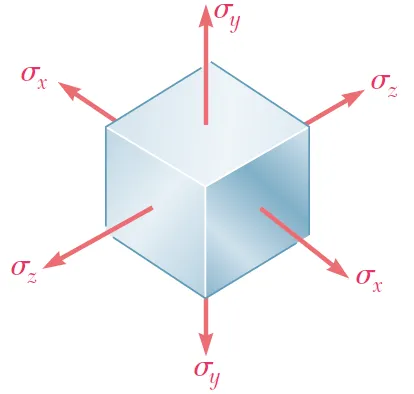
下面说说复杂应力状态下(如三向应力状态)的泊松比,即 \sigma _{x} \ne 0 ,\sigma _{y} \ne 0 ,\sigma _{z} \ne 0 ,如图4所示。
图4
多向应力状态
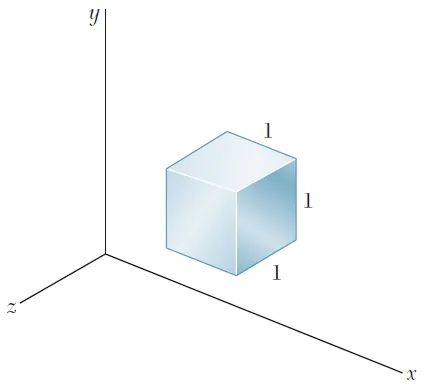
图5
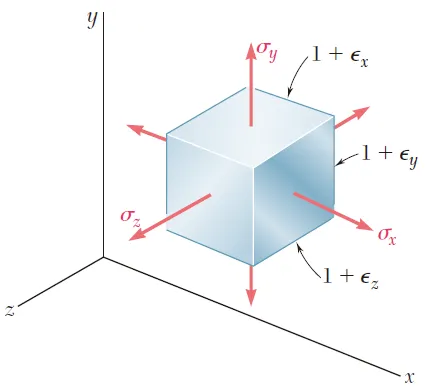
我们假设图5中各边均为单位长度的立方体,在三向拉力作用下,它将发生变形形成直角平行六面体,相应地x、y、z方向的边长分别变为 1+\varepsilon _{x} 、1+\varepsilon _{y} 、1+\varepsilon _{z} 。
图6
为了综合考虑所有应力因素对各个方向应变的影响,我们对各个应力先单独考虑其对其它方向应变的影响,然后再将所有因素叠加起来。
我们以x方向为例。
根据公式(1)和公式(4)我们得到:
\sigma _{x} 将导致:
x方向应变 \varepsilon _{x} =\frac{\sigma _{x} }{E} ;
y方向应变 -\frac{v\sigma _{x} }{E} ;
z方向应变 -\frac{v\sigma _{x} }{E} 。
\sigma _{y} 将导致:
x方向应变 -\frac{v\sigma _{y} }{E} ;
y方向应变 \varepsilon _{y} = \frac{\sigma _{y}}{E} ;
z方向应变 -\frac{v\sigma _{y} }{E} 。
\sigma _{z} 将导致:
x方向应变 -\frac{v\sigma _{z} }{E} ;
y方向应变 -\frac{v\sigma _{z} }{E} ;
z方向应变 \varepsilon _{z} =\frac{\sigma _{z} }{E} 。
把上面所有影响进行叠加,会得到三向应力状态下各个方向的应变为:
\varepsilon _{x} =+\frac{\sigma _{x} }{E}-\frac{v\sigma _{y} }{E} -\frac{v\sigma _{z} }{E} (5)
\varepsilon _{y} =-\frac{v\sigma _{x} }{E}+\frac{\sigma _{y} }{E} -\frac{v\sigma _{z} }{E} (6)
\varepsilon _{z} =-\frac{v\sigma _{x} }{E}-\frac{v\sigma _{y} }{E} +\frac{\sigma _{z} }{E} (7)