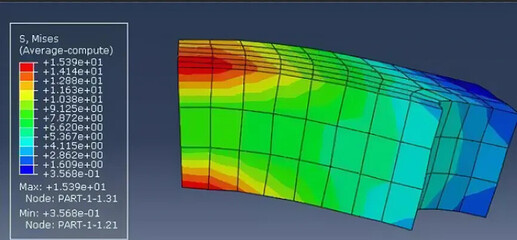
有限元分析应力云图时经常会用到Mises准则,如图1左上角所示,这个Mises准则就是“最大畸变能理论”。
图1 Mises准则分析应力
“最大畸变能理论”翻译自英文“Maximum Distortion Energy Criterion”,又被称作von Mises Criterion,即“凡·米塞斯理论(准则)”。
它是由德裔美国人,应用数学家,Richard von Mises提出的理论。
这个理论说的通俗点就是:材料拉伸试验中,导致材料进入屈服阶段的原因是外荷载做功——对试件单位体积产生了致使其变形的能量,当同样材料的结构构件或机械部件受到的外荷载作用时,该外荷载所产生的能量,同样会对该构件单位体积产生一定的能量,只要这个能量小于材料屈服时所需要的能量,那么该构件就是安全的。
因此,理解这个理论的前提是要明白两件事:
如何从能量角度解释材料屈服?
什么是“材料屈服所需要的单位体积能量”?
这个理论的英文描述中有个“distortion”,它的意思是“变形”,那么这句英文翻译的更直白一点大意就是:“引起材料变形所需的能量”的理论。
提起“变形”,会自然想到“应变”,这个理论必然是与应变和能量挂钩的。
应变自不必多说,那么为什么材料屈服会和能量扯上关系?这是理解“最大畸变能理论”的关键所在。
有关上面两个问题,“最大畸变能理论”的关键部分在抗剪强度=0.58×抗拉强度的原因 中查看(声明:文末“这就是最大畸变能密度理论,也被成为第四强度理论”为笔误,应改为“这就是最大畸变能理论,也被称为第四强度理论”)。
在那边帖子的末尾,公式(32)是三轴应力状态下材料是否屈服的判定准则,而对于平面应力状态,σc=0,因此公式(32)可简化成:
\sigma _{a} ^{2} - \sigma _{a} \sigma _{b} +\sigma _{b} ^{2} <\sigma _{y} ^{2}
\sigma _{y} 是材料屈服强度。
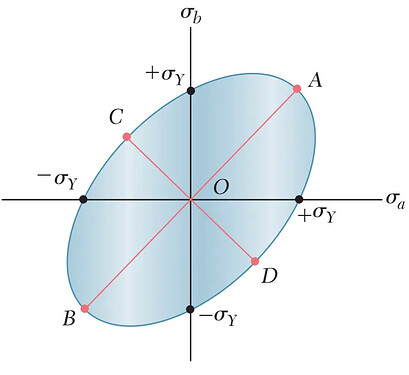
作为材料屈服的边界条件,\sigma _{a} ^{2} - \sigma _{a} \sigma _{b} +\sigma _{b} ^{2} <\sigma _{y} ^{2} 是一椭圆曲线,如图2所示。用图2可以更直观地解释最大畸变能理论:平面应力状态下的两个主应力坐标位于该曲线上或之外,材料会进入屈服阶段;相反,两个主应力坐标位于阴影区域内,构件则是安全的。
图2 最大畸变能理论
和“最大剪应力理论”一样,该理论同样适用于塑性材料。