尖角周围的电磁加热
使用 COMSOL Multiphysics® 软件求解的最常见问题之一是电磁加热问题,它耦合了麦克斯韦方程(用于求解电流和总损耗)和传热方程(用于求解温度曲线)的解。
随着网格细化,尖角周围损耗的积分将收敛。这是以“弱形式”求解控制方程的有限元方法的优点之一,它满足积分意义上的控制偏微分方程:最小化模型中的总误差,但允许(可能是无穷)局部误差。
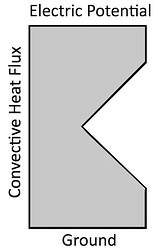
一个简单的电磁加热问题示意图,内尖角处有一个奇点。如上图所示,让我们通过一个简单的示例来复习奇点的概念。一个带尖锐内角缺口的矩形域上施加的电位差导致电流流动和材料中的电阻损耗。
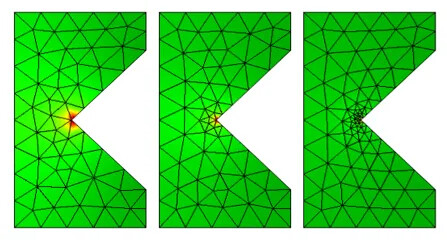
在下图中,我们看到了电阻损耗的彩色绘图,以及内尖角处使用的不同级别的细化网格。在最高级别的细化网格处,尖角附近的小范围区域出现损耗。
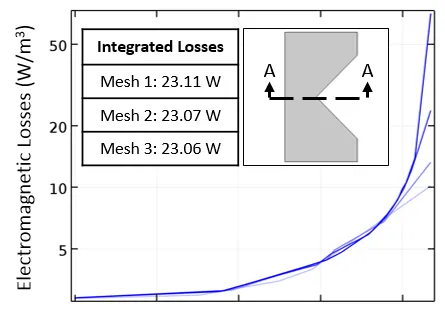
几种不同的网格产生的电磁损耗。理论上电场在这个内尖角处是无限大的,因为这种几何形状和边界条件意味着电流必须在某一点瞬间改变方向。需要注意的是,外尖角不会导致奇点。由于几何形状和边界条件的原因,电流在这些点不会被迫瞬间改变方向。
沿切线绘制的用对数标尺表示的电阻损耗图,以及使用不同的细化网格产生的损耗积分表。如上图所示,如果在横截面上绘制损耗,可以观察到随着网格的细化,尖点处的损耗越来越大。然而,域上的损耗积分(简单来说,就是曲线下方的区域)会随着网格细化快速地收敛。
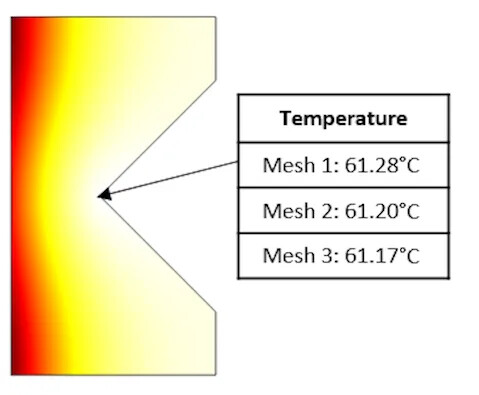
现在,通过额外求解稳态条件下的温度分布传热方程,将这个问题变成一个多物理场问题。下图绘制了使用不同级别的细化网格求解的温度场,以及尖点处的温度。
使用不同级别的细化网格计算的温度场和尖角处的温度值表格。从上述结果可以看出,奇点处的温度(当然还有其他地方)对网格细化程度也极不敏感,原因有两个:
首先,正如我们看到的,总电阻损耗对网格非常不敏感。
其次,只要总热载荷接近,稳态传热控制方程的扩散性质将返回非常接近的温度解。
另一方面,如果热载荷非常高,瞬态温度解可以预测非常高的局部温度,但这也是一个局部的和相对的效应,尽管是在时间上。也就是说,空间热载荷分布的尖峰将随着时间的推移而被平滑,并且在非常长的求解时间下,瞬态解将接近稳态解。