背景
1676年,大清康熙十五年。大洋彼岸的英国科学家,也是应用力学奠基人之一,罗伯特·胡克利用弹簧试验发现应力(荷载)的增长会导致应变(变形)线性增加,这就是早期的胡克定律。该发现可以表达为以下公式:
σ=Eε
公式中的E代表的是应力-应变曲线中,线弹性阶段的斜率,叫做弹性模量或杨氏模量,由英国科学家托马斯·杨在1807年首先发布。
我们知道应变大小上等于伸长量与原长度之比,属于无量纲参数,因此弹性模量的单位与应力一样,也是帕斯卡P。
胡克定律的适用条件
胡克定律的适用条件是,材料在受力情况下的应力不超过材料的比例极限(注意区别于屈服强度),这一点很重要,它和我们实际工程设计息息相关。
比如细心的同行会注意到,在国家规范里面,HRB400的螺纹钢筋,虽然屈服强度是400MPa,但是其设计强度却只有360MPa,想必就是这个原因——钢筋的比例极限能确保工程设计中材料完全处于弹性阶段,以便适用胡克定律进行弹性设计,确保构件在服役过程中变形可控。
欧洲标准也是这样,例如对于一般工程钢材,会取约1.2的材料安全分项系数,确保材料在受力时完全处于弹性工作阶段。
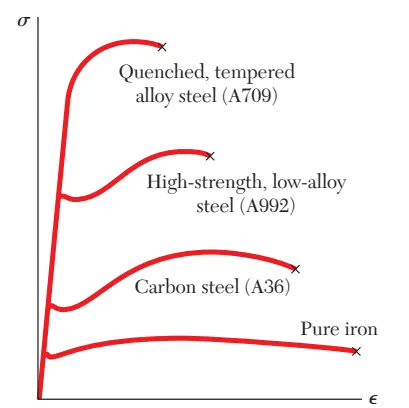
材料的强度、延展性以及耐腐蚀性,受到合金元素、热处理工艺以及加工工艺的影响很大。但是弹性模量不同,如图1所示,纯铁、碳钢、高强低合金钢和经过热处理的合金钢,在强度、延展性两方面差异可以很大,但是它们在弹性阶段的弹性模量却是一致的。
图1 不同材料应力-应变曲线
简单来说,相同尺寸的结构构件,增加材料强度可以提高承载力,但是结构的刚度不变、变形不变。
另外值得特别说明的是,对于各向同性材料来说,无论哪个加载方向的弹性模量都一样,但是对于各向异性材料,加载方向不同,表现出来的弹性模量也不同。
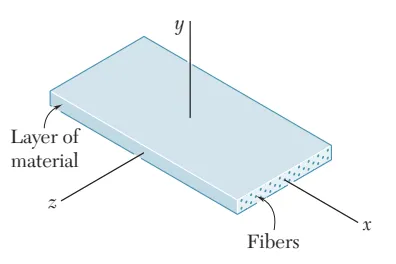
当前建筑市场活跃着很多复合型材料。典型如FRP,它是由玻璃纤维或碳纤维等材料和各类树脂材料复合而成,如图2所示。
图2 纤维复合材料
这种材料的特点是所有纤维方向一致(如x方向)以便让复合材料获取最大承载力。纤维的优势在于强度和刚度都很高,沿着x方向加载时,复合材料整体表现出来的承载力和弹性模量也很大。
但是y方向却相反,沿y方向施加荷载,荷载方向垂直于纤维长度方向,并不会发挥纤维的强度和刚度,只有树脂的强度和刚度产生贡献,因此复合材料的y方向无论承载力和弹性模量都远不及x方向。
弹性模量的本质
弹性模量本质上是材料原子间力的体现。
图3 原子间力
弹性阶段
当材料处于完全弹性阶段时,施加荷载会使原子间发生相对位移但是原子键依然完好,荷载消失,原子之间相对位移消失,材料完全恢复原始尺寸。
塑性阶段
当施加荷载过大使材料进入塑性阶段,部分原子键被破坏,部分原子键没有被破坏(注:如果所有原子键都破坏意味着材料发生了断裂)。
当荷载消失,原子键被破坏导致原子之间产生永久位移,原子键没有被破坏的原子间位移依然可以恢复原状,这就是为什么进入塑性变形的材料随着荷载消除依然会回弹一部分变形同时产生部分永久变形。
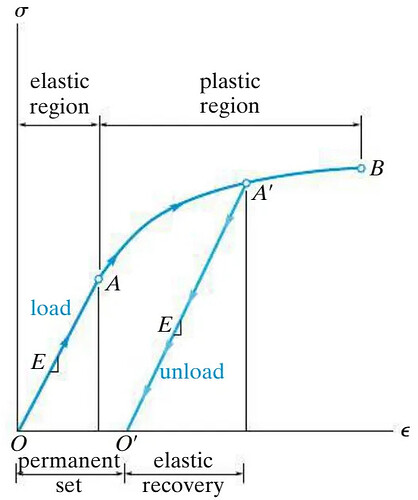
值得说明的是,虽然部分原子键被破坏,但是荷载消除之后,被破坏原子键的原子会和其它原子之间重新产生原子键达到平衡,当再次施加荷载时,该材料会重复和材料未变形时内部原子之间相同的行为模式,即弹性阶段原子之间继续产生相对位移,弹性模量不变,但是屈服强度会变大(晶体结构发生变化所致)、延展性降低,如图4所示。利用这个原理可增加材料屈服强度,这种现象叫做应力硬化,也叫作冷作硬化。
图4 加载至A’卸载,再加载(O’A’B段)
这个本质也解释了为什么我们上面图1说不同种类的钢材强度不同,但是弹性模量相同。因为所有的钢材成分绝大部分都是铁元素,其它合金元素占比很小,导致它们对原子间力的影响微乎其微,不足以影响弹性模量。
也正是这个原因,橡胶等有机物的弹性模量要小得多。因为有机物材料都是有机大分子构成,而分子间力远小于原子间力、分子数量远小于原子数量,因此弹性模量也小得多。