物体相对于不同参考系的运动是不相同的。
研究物体相对于不同参考系的运动分析物体相对于不同参考系运动之间的关系,可称之为复杂运动或合成运动。
1 相对运动 - 牵连运动 - 绝对运动
物体的运动对于不同的参考体来说是不同的。
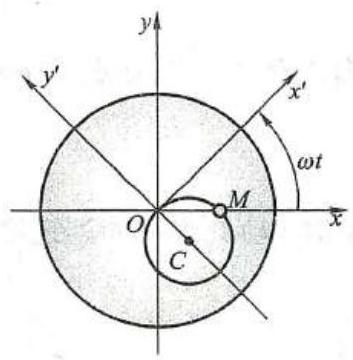
如图 1 所示沿直线轨道滚动的车轮,其轮缘上点 M 的运动,对于地面上的观察者来说,点的运动轨迹是旋轮线但是对于车上的观察者来说点的运动轨迹则是一个圆。
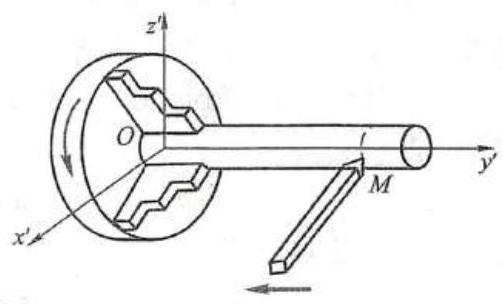
又如图 2 所示车床在工作时车刀刀尖 M 相对于地面是直线运动但是它相对于旋转的工件来说却是圆柱面螺旋运动因此车刀在工件的表面上切出螺旋线。显然在上述各例中,动点 M 相对于两个参考体的速度和加速度也都不同。
图 1
图 2
通过观察可以发现物体对一参考体的运动可以由几个运动组合而成。
例如在上述的例子中,车轮上的点 M 是沿旋轮线运动,但是如果以车厢作为参考体,则点 M 相对于车厢的运动是简单的圆周运动,车厢相对于地面的运动是简单的平移。这样,轮缘上一点的运动就可以看成为两个简单运动的合成,即点 M 相对于车厢做圆周运动同时车厢相对地面做平移。于是相对于某一参考体的运动可由相对于其他参考体的几个运动组合而成这种运动称为合成运动。
习惯上把固定在地球上的坐标系称为定参考系,简称定系,以 {Oxyz} 坐标系表示;固定在其他相对于地球运动的参考体上的坐标系称为动参考系简称动系以 {O}^{\prime }{x}^{\prime }{y}^{\prime }{z}^{\prime } 坐标系表示。
在上述的前一例中,动参考系固定在车厢上;在后一例中,动参考系则固定在工件上。
用点的合成运动理论分析点的运动时必须选定两个参考系以区分三种运动:
(1)动点相对于定参考系的运动称为绝对运动;
(2) 动点相对于动参考系的运动,称为相对运动;
(3) 动参考系相对于定参考系的运动,称为牵连运动。
仍以滚动的车轮为例,取轮缘上的一点 M 为动点,固结于车厢的坐标系为动参考系,则车厢相对于地面的平移是牵连运动;在车厢上看到点做圆周运动这是相对运动;在地面上看到点沿旋轮线运动这是绝对运动。
注意在分析这三种运动时必须明确:
(1)站在什么地方看物体的运动;
(2)看什么物体的运动。
应该指出动点的绝对运动和相对运动都是指点的运动它可能做直线运动或曲线运动;而牵连运动则是参考体的运动,实际上是刚体的运动,它可能做平移、转动或其他较复杂的运动。
下面介绍一下三种运动的数学描述方法。
1.1 绝对运动
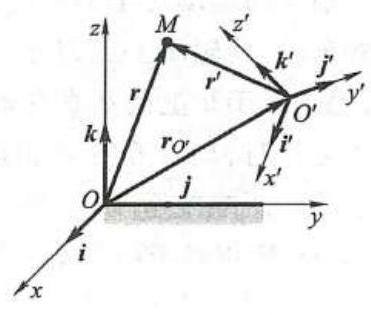
图 3 中,动点 M 的绝对运动可以用它在定参考系 {Oxyz} 的运动方程来描述,即
图 3
式 (1) 称为绝对运动方程。消去时间 t ,得到点 M 在定参考系中的运动轨迹称为绝对运动轨迹。
设 \mathbf{i}\text{、}\mathbf{j}\text{、}\mathbf{k} 是沿 x\text{、}y\text{、}z 轴正向的三个单位矢量 (基矢量)\mathbf{r} 为动点 M 在定参考系中的矢径于是有
则绝对运动方程也可以写成
动点 M 相对于定参考系的速度为
式 (3) 称为动点 M 的绝对速度,其中下标 “ \mathrm{a} ” 表示 “绝对”。动点 M 的绝对加速度为
1.2 相对运动
动点 M 的相对运动可以用它在动参考系 {O}^{\prime }{x}^{\prime }{y}^{\prime }{z}^{\prime } 中的运动方程来描述,即
式 (5) 称为相对运动方程。消去时间 t ,得到动点 M 在动参考系中的运动轨迹称为相对运动轨迹。
设 {i}^{\prime }\text{、}{j}^{\prime }\text{、}{k}^{\prime } 是沿 {x}^{\prime }\text{、}{y}^{\prime }\text{、}{z}^{\prime } 轴正向的三个单位矢量 (基矢量){\mathbf{r}}^{\prime } 为动点 M 在动参考系中的矢径,从而有
动点 M 的相对速度为
其中下标 “ \mathrm{r} ” 表示 “相对”。由于在动参考系中只能观察到动点 M 相对于动参考系的运动,也就是动点 M 在动参考系中的坐标随时间的变化,因此上式在对时间求导数时将动参考系的三个基矢量 {\mathbf{i}}^{\prime } 、 {\mathbf{j}}^{\prime } 、 {\mathbf{k}}^{\prime } 视为常矢量,这种导数称为相对导数,在导数符号上加 “~” 表示。
凡是在导数符号上加上这一符号均代表相对导数它反映了在动参考系中所观察到的对应物理量随时间的变化情况。
动点 M 的相对加速度为
1.3 牵连运动
牵连运动是动参考系相对于定参考系的运动是刚体的运动其运动可以用刚体的运动方程来描述。例如若动参考系做定轴转动其运动方程可以写为
其中 \varphi 为刚体的转角。
由于动参考系的运动是刚体的运动而不是一个点的运动所以除非动参考系做平移,否则其上各点的运动都不完全相同。因为动参考系与动点直接相关的是该瞬时动参考系上与动点相重合的那一点,因此定义 t 瞬时动参考系上与动点相重合的那一点为该瞬时动点的牵连点牵连点的速度和加速度分别称为该瞬时动点的牵连速度和牵连加速度,分别用 {v}_{\mathrm{e}} 和 {a}_{\mathrm{e}} 来表示,其中下标 “ \mathrm{e} ” 表示 "牵连”。
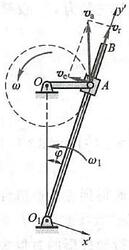
现在举例说明牵连速度和牵连加速度的概念。设水从喷管射出,喷管又绕 O 轴转动,转动角速度为 \omega ,角加速度为 \alpha 如图 4 所示。将动参考系固定在喷管上,取水滴 M 为动点。显然,动点相对于喷管的运动为直线运动因此相对运动轨迹为直线 {OA} ,相对速度 {v}_{\mathrm{r}} 和相对加速度
图 4
{a}_{\mathrm{r}} 都沿喷管 {OA} 方向。至于牵连速度 {v}_{\mathrm{e}} 和牵连加速度 {a}_{\mathrm{e}} ,则是喷管上与动点 M 重合的那一点 (牵连点) 的速度和加速度。喷管绕 O 轴转动,因此,牵连速度 {v}_{\mathrm{e}} 的大小为
方向垂直于喷管,指向转动的一方。牵连加速度 {a}_{\mathrm{e}} 的大小为
它的方向与喷管之间的夹角为
偏向 \alpha 所指的一边。
1.4 点的绝对运动与相对运动之间的关系
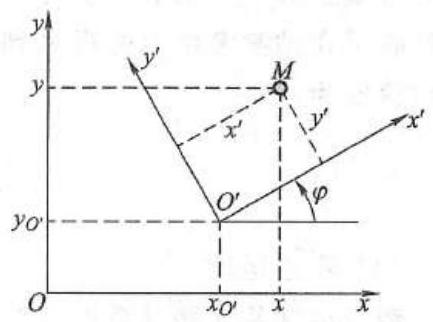
点的绝对运动与相对运动是动点相对于不同参考系的运动可以利用坐标变换来建立两者之间的关系。以平面问题为例,设 {Oxy} 是定参考系 {O}^{\prime }{x}^{\prime }{y}^{\prime } 是动参考系 M 是动点,如图 5 所示。动点 M 的绝对运动方程为
图 5
动点 M 的相对运动方程为
动参考系相对于定参考系的运动可以由如下三个方程完全描述:
这三个方程称为牵连运动方程 (刚体运动方程)其中 \varphi 角是从 x 轴到 {x}^{\prime } 轴的转角,以逆时针方向为正。由图 5 可得动参考系 {O}^{\prime }{x}^{\prime }{y}^{\prime } 与定参考系 {Oxy} 之间的坐标变换关系为
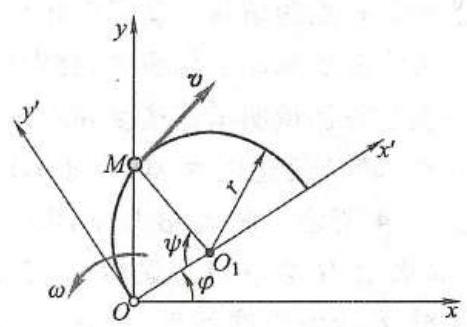
例 1 点 M 相对于动参考系 O{x}^{\prime }{y}^{\prime } 沿半径为 r 的圆周以速度 v 做匀速圆周运动 (圆心为 {O}_{1} ),动参考系 O{x}^{\prime }{y}^{\prime } 相对于定参考系 {Oxy} 以匀角速度 \omega 绕点 O 做定轴转动,如图 6 所示。初始时 O{x}^{\prime }{y}^{\prime } 与 {Oxy} 重合,点 M 与点 O 重合。求点 M 的绝对运动方程。
图 6
解: 连接 {O}_{1}M ,由图 6 可知
\psi = \frac{vt}{r}于是得点 M 的相对运动方程为
{x}^{\prime } = O{O}_{1} - {O}_{1}M \cdot \cos \psi = r\left( {1 - \cos \frac{vt}{r}}\right){y}^{\prime } = {O}_{1}M \cdot \sin \psi = r\sin \frac{vt}{r}牵连运动方程为
{x}_{{0}^{\prime }} = {x}_{0} = 0,\;{y}_{{0}^{\prime }} = {y}_{0} = 0,\;\varphi = {\omega t}利用坐标变换关系式 (9),得点 M 的绝对运动方程为
x = r\left( {1 - \cos \frac{vt}{r}}\right) \cos {\omega t} - r\sin \frac{vt}{r}\sin {\omega t}y = r\left( {1 - \cos \frac{vt}{r}}\right) \sin {\omega t} + r\sin \frac{vt}{r}\cos {\omega t}
例 2 已知点 M 在平面内运动,其绝对运动方程为
x = 5{t}^{2} + {2t}\cos {4t} - 6{t}^{2}\sin {4t},\;y = {3t} + {2t}\sin {4t} + 6{t}^{2}\cos {4t}点 M 相对于动参考系 {O}^{\prime }{x}^{\prime }{y}^{\prime } 的相对运动方程为
{x}^{\prime } = {2t},\;{y}^{\prime } = 6{t}^{2}求动参考系原点 {O}^{\prime } 的运动方程和动参考系坐标轴的转动方程(牵连运动方程)。
解: 将 x\text{、}y 和 {x}^{\prime }\text{、}{y}^{\prime } 代入坐标变换关系式 (9),得
5{t}^{2} + {2t}\cos {4t} - 6{t}^{2}\sin {4t} = {x}_{{0}^{\prime }} + {2t}\cos \varphi - 6{t}^{2}\sin \varphi{3t} + {2t}\sin {4t} + 6{t}^{2}\cos {4t} = {y}_{{0}^{ * }} + {2t}\sin \varphi + 6{t}^{2}\cos \varphi比较上式等号两端可知牵连运动方程为
{x}_{{0}^{\prime }} = 5{t}^{2},\;{y}_{{0}^{\prime }} = {3t},\;\varphi = {4t}本例各式中,位移以 \mathrm{m} 计,时间以 \mathrm{s} 计,角度以 \mathrm{{rad}} 计。
例 3 用车刀切削工件的直径端面,车刀刀尖 M 沿水平轴 x 做往复运动,如图 7 所示。设 {Oxy} 为定参考系,刀尖的运动方程为 x = b\sin {\omega t} 。工件以匀角速度 \omega 逆时针转向转动。求车刀在工件圆端面上切出的痕迹。
图 7
解:根据题意,需求车刀刀尖 M 相对于工件的运动轨迹方程。
设刀尖 M 为动点,动参考系固定在工件上。则动点 M 在动参考系 O{x}^{\prime }{y}^{\prime } 和定参考系 {Oxy} 中的坐标关系为
{x}^{\prime } = x\cos {\omega t},\;{y}^{\prime } = - x\sin {\omega t}将点 M 的绝对运动方程代入上式中,得
{x}^{\prime } = b\sin {\omega t}\cos {\omega t} = \frac{b}{2}\sin {2\omega t}{y}^{\prime } = - b{\sin }^{2}{\omega t} = - \frac{b}{2}\left( {1 - \cos {2\omega t}}\right)上式就是车刀相对于工件的运动方程。
从上式中消去时间 t ,得刀尖的相对运动轨迹方程为
{\left( {x}^{\prime }\right) }^{2} + {\left( {y}^{\prime } + \frac{b}{2}\right) }^{2} = \frac{{b}^{2}}{4}可见,车刀在工件上切出的痕迹是一个半径为 \frac{b}{2} 的圆,该圆的圆心 C 在动坐标轴 {y}^{\prime } 轴上,圆周通过工件的中心 O 。
2 点的速度合成定理
下面研究点的相对速度、牵连速度和绝对速度三者之间的关系。
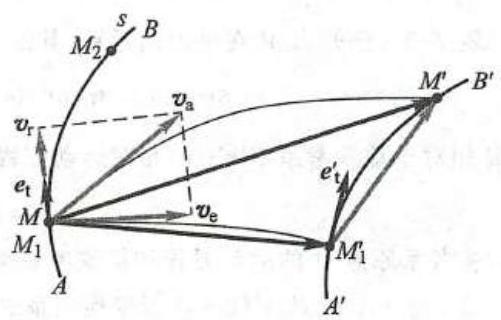
设动点 M 的相对运动轨迹为曲线 {AB} ,为了容易理解,设想 {AB} 为一金属线,动参考系即固定在此线上而将动点看成是沿金属线滑动的一极小圆环,如图 8 所示。
图 8
在瞬时 t ,动点与曲线 {AB} 上的点 {M}_{1} 重合,点 {M}_{1} 也称为该瞬时动点的牵连点。经过极短的时间间隔 {\Delta t} 后,曲线 {AB} 运动到新位置 {A}^{\prime }{B}^{\prime } ;同时,动点沿弧 \overset{⏜}{MM}{}^{\prime } 运动到点 {M}^{\prime } 而点 {M}_{1} 则随动参考系运动到点 {M}_{1}^{\prime } 。
由图中的几何关系有
式 (10) 通过引入牵连点 {M}_{1} ,建立了动点绝对运动与相对运动之间的联系。以 {\Delta t} 除上式两端,并令 {\Delta t} \rightarrow 0 ,取极限,得
根据速度的定义,动点 M 在瞬时 t 的绝对速度为
而瞬时 t 动点 M 的牵连速度为
显然下一步推导的关键在于
与瞬时 t 动点 M 的相对速度之间的关系。
由于金属线就是动点 M 的相对运动轨迹,因此相对运动方程可用定义在金属线上的弧坐标来表示
由于弧坐标是定义在运动轨迹上的代数量因此在不同参考系下其运动方程具有相同的形式。
设瞬时 t ,金属线在点 {M}_{1} 的切向基矢量为 {\mathbf{e}}_{1} ,则由点的速度在自然轴系中的表达式相对速度可以写为
经过极短的时间间隔 {\Delta t} 后,点 {M}_{1} 则随金属线运动到点 {M}_{1}^{\prime } ,此时点 {M}_{1}^{\prime } 沿曲线的切向基矢量为 {\mathbf{e}}_{\mathrm{t}}^{\prime } 。设弧长 \overset{⏜}{{M}_{1}^{\prime }{M}^{\prime }} = {\Delta s} ,而基矢量 {\mathbf{e}}_{\mathrm{t}} 与 {\mathbf{e}}_{\mathrm{t}}^{\prime } 之间的夹角为 {\Delta \theta } ,显然有
从而有
将式(12)、式(13)和式(15)代入式(11),得到
由此得到点的速度合成定理: 动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速度的矢量和。即动点的绝对速度可以由牵连速度与相对速度所构成的平行四边形的对角线来确定。这个平行四边形称为速度平行四边形。
通过引入牵连点来建立动点绝对运动与相对运动之间的联系是点的合成运动的一种主要的分析方法。下面结合图 3对这种分析方法做进一步的介绍。设动参考系的坐标原点 {O}^{\prime } 在定参考系中的矢径为 {r}_{{O}^{\prime }} ,沿动参考系坐标轴的三个单位矢量分别为 {\mathbf{i}}^{\prime }\text{、}{\mathbf{j}}^{\prime }\text{、}{\mathbf{k}}^{\prime } ,动点 M 在定参考系中的矢径为 \mathbf{r} ,在动参考系中的矢径为 {\mathbf{r}}^{\prime } 由图中几何关系有
记瞬时 t 动点 M 的牵连点为 {M}_{1} ,由于该瞬时点 {M}_{1} 与动点 M 相重合,因此点 {M}_{1} 在动参考系中的坐标即为该瞬时动点在动参考系中的坐标 {x}^{\prime }\text{、}{y}^{\prime }\text{、}{z}^{\prime } 。注意到点 {M}_{1} 是动参考系上的一点,它在动参考系中的坐标是常数,故点 {M}_{1} 在定参考系中的运动方程为
其中 {r}_{1} 表示点 {M}_{1} 在定参考系中的矢径 {r}_{1}^{\prime } 表示点 {M}_{1} 在动参考系中的矢径,下标 C 表示“常数”,由此得到牵连速度的表达式为
将式 (17) 两边对 t 求导数,并代入式 (3)、式 (7) 和式 (19),就得到式 (16)的结果。同样,上述推导过程中并未限制动参考系做什么样的运动,因此点的速度合成定理适用于牵连运动是任何运动的情况即动参考系可做平移、转动或其他任何较复杂的运动。
下面举例说明点的速度合成定理的应用。
例 4 刨床的急回机构如图 9 所示。曲柄 {OA} 的一端 A 与滑块用铰链连接。当曲柄 {OA} 以匀角速度 \omega 绕固定轴 O 转动时,滑块在摇杆 {O}_{1}B 上滑动,并带动摇杆 {O}_{1}B 绕固定轴 {O}_{1} 摆动。设曲柄 {OA} 长为 r ,两轴间距离 O{O}_{1} = l 。求当曲柄 {OA} 在水平位置时摇杆 {O}_{1}B 的角速度 {\omega }_{1} 。
图 9
解: 在本题中应选取曲柄 {OA} 端点 A 作为研究的动点,把动参考系 {O}_{1}{x}^{\prime }{y}^{\prime } 固定在摇杆 {O}_{1}B 上,并与摇杆 {O}_{1}B 一起绕 {O}_{1} 轴摆动。
点 A 的绝对运动是以点 O 为圆心的圆周运动,相对运动是沿摇杆 {O}_{1}B 方向的直线运动,而牵连运动则是摇杆 {O}_{1}B 绕 {O}_{1} 轴的摆动。
于是,绝对速度 {v}_{\mathrm{a}} 的大小和方向都是已知的,它的大小等于 {r\omega } 方向与曲柄 {OA} 垂直;相对速度 {v}_{\mathrm{r}} 的方向是已知的,即沿 {O}_{1}B ;而牵连速度 {v}_{\mathrm{e}} 是摇杆 {O}_{1}B 上与点 A 重合的那一点的速度,它的方向垂直于摇杆 {O}_{1}B ,也是已知的。共计有四个要素已知。由于 {v}_{a} 的大小和方向都已知因此这是一个速度分解的问题。
根据点的速度合成定理,做出速度平行四边形,如图 9 所示。由其中的三角关系可求得
{v}_{\mathrm{e}} = {v}_{\mathrm{a}}\sin \varphi又 \sin \varphi = \frac{r}{\sqrt{{l}^{2} + {r}^{2}}} ,且 {v}_{\mathrm{a}} = {r\omega } ,所以有
{v}_{\mathrm{e}} = \frac{{r}^{2}\omega }{\sqrt{{l}^{2} + {r}^{2}}}设摇杆 {O}_{1}B 在此瞬时的角速度为 {\omega }_{1} ,则
{v}_{\mathrm{e}} = {O}_{1}A \cdot {\omega }_{1} = \frac{{r}^{2}\omega }{\sqrt{{l}^{2} + {r}^{2}}}其中 {O}_{1}A = \sqrt{{l}^{2} + {r}^{2}} 。
由此得出此瞬时摇杆 {O}_{1}B 的角速度为
{\omega }_{1} = \frac{{r}^{2}\omega }{{l}^{2} + {r}^{2}}方向如图所示。
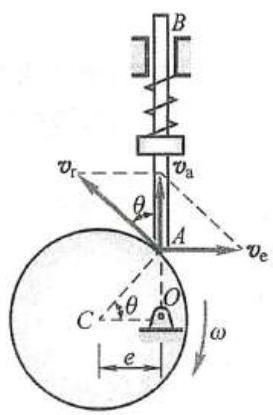
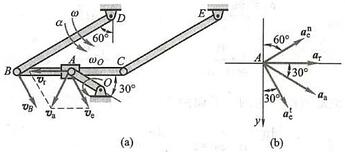
例 5 如图 10 所示,半径为 R 、偏心距为 e 的凸轮,以匀角速度 \omega 绕 O 轴转动,杆 {AB} 能在滑槽中上下平移,杆的端点 A 始终与凸轮接触,且 {OAB} 成一直线。求在图示位置时,杆 {AB} 的速度。
解: 因为杆 {AB} 做平移,各点速度相同,所以只要求出其上任一点的速度即可。选取杆 {AB} 的端点 A 作为研究的动点,动参考系随凸轮一起绕 O 轴转动。
图 10
点 A 的绝对运动是直线运动,相对运动是以凸轮中心 C 为圆心的圆周运动,牵连运动则是凸轮绕 O 轴的转动。
于是,绝对速度方向沿杆 {AB} ,相对速度方向沿凸轮圆周的切线而牵连速度为凸轮上与杆 {AB} 端点 A 重合的那一点的速度,它的方向垂直于 {OA} ,它的大小为 {v}_{\mathrm{e}} = \omega \cdot {OA} 。根据点的速度合成定理,已知四个要素即可做出速度平行四边形如图 10 所示。由三角关系求得杆 {AB} 的绝对速度为
{v}_{\mathrm{n}} = {v}_{\mathrm{e}}\cot \theta = \omega \cdot {OA}\frac{e}{OA} = {\omega e}
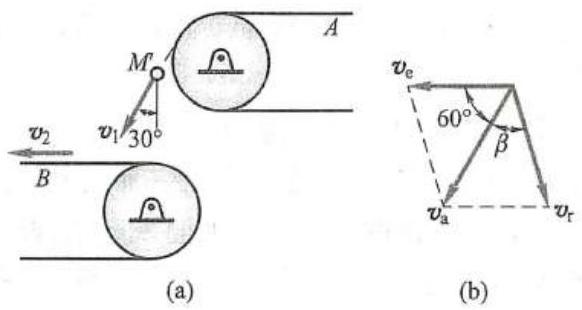
例 6 矿砂从传送带 A 落到另一传送带 B 上,如图 11a 所示。站在地面上观察矿砂下落的速度为 {v}_{1} = 4\mathrm{\;m}/\mathrm{s} ,方向与铅垂线成 {30}^{ \circ } 角。已知传送带 B 的水平传动速度 {v}_{2} = 3\mathrm{\;m}/\mathrm{s} 。求矿砂相对于传送带 B 的速度。
图 11
解: 以矿砂 M 为动点,动参考系固定在传送带 B 上。矿砂相对地面的速度 {v}_{1} 为绝对速度;牵连速度应为动参考系上与动点相重合的那一点的速度。由于动参考系为无限大且作平移因此各点速度都等于 {v}_{2} 。于是 {v}_{2} 等于动点 M 的牵连速度。
由点的速度合成定理知,三种速度形成平行四边形,绝对速度必须沿对角线,因此作出的速度平行四边形如图 11b 所示。根据几何关系求得
{v}_{\mathrm{r}} = \sqrt{{v}_{\mathrm{e}}^{2} + {v}_{\mathrm{a}}^{2} - 2{v}_{\mathrm{e}}{v}_{\mathrm{a}}\cos {60}^{ \circ }} = {3.6}\mathrm{\;m}/\mathrm{s}{v}_{\mathrm{r}} 与 {v}_{\mathrm{a}} 间的夹角为
\beta = \arcsin \left( {\frac{{v}_{\mathrm{e}}}{{v}_{\mathrm{r}}}\sin {60}^{ \circ }}\right) = {46}^{ \circ }{12}^{\prime }图 12
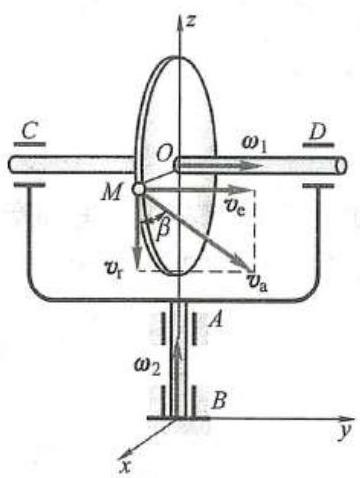
例 7 圆盘半径为 R ,以角速度 {\omega }_{1} 绕水平轴 {CD} 转动支承 {CD} 的框架又以角速度 {\omega }_{2} 绕铅垂的 {AB} 轴转动,如图 12 所示。圆盘垂直于 {CD} 轴,圆心在 {CD} 轴与 {AB} 轴的交点 O 处。求当连线 {OM} 在水平位置时,圆盘边缘上的点 M 的绝对速度。
解: 以点 M 为动点,动参考系与框架固结。点 M 的相对运动是以点 O 为圆心、在铅垂平面内的圆周运动,相对速度垂直于 {OM} ,方向朝下,大小为
{v}_{\mathrm{r}} = R{\omega }_{1}点 M 的牵连速度应为动参考系上与动点 M 相重合的那一点的速度,是绕 z 轴以角速度 {\omega }_{2} 转动的动参考系上该点的速度因此有
{v}_{\mathrm{e}} = R{\omega }_{2}速度矢 {v}_{\mathrm{e}} 在水平面内,垂直于半径 {OM} ,于是 {v}_{\mathrm{e}} 垂直 {v}_{\mathrm{r}} 。根据点的速度合成定理,即
{v}_{\mathrm{a}} = {v}_{\mathrm{e}} + {v}_{\mathrm{r}}得
{v}_{\mathrm{a}} = \sqrt{{v}_{\mathrm{e}}^{2} + {v}_{\mathrm{r}}^{2}} = R\sqrt{{\omega }_{2}^{2} + {\omega }_{1}^{2}}\tan \beta = \frac{{v}_{\mathrm{e}}}{{v}_{\mathrm{r}}} = \frac{{\omega }_{2}}{{\omega }_{1}}式中的 \beta 为 {v}_{\mathrm{a}} 与铅垂线间的夹角。
总结以上各例的解题步骤如下:
(1)选取动点、动参考系和定参考系。所选的动参考系应能将动点的运动分解成为相对运动和牵连运动。因此动点和动参考系不能选在同一个物体上一般应使相对运动易于看清。
(2)分析三种运动和三种速度。相对运动是怎样的一种运动(直线运动、圆周运动、或其他某种曲线运动)? 牵连运动是怎样的一种运动(平移、转动、或其他某一种刚体运动)? 绝对运动是怎样的一种运动(直线运动、圆周运动、或其他某一种曲线运动)? 各种运动的速度都有大小和方向两个要素只有已知四个要素时才能画出速度平行四边形。
(3)应用点的速度合成定理,做出速度平行四边形。必须注意,做图时要使绝对速度成为平行四边形的对角线。
(4)利用速度平行四边形中的几何关系解出未知数。
3 点的加速度合成定理
式(18)通过分析牵连点运动来建立点的绝对运动与相对运动的关系,这一分析方法可进一步用于点的加速度合成定理的推导。将式 (16) 两边对时间 t 求导数得
下面分别计算相对速度和牵连速度对时间的导数。将式 (7) 两边对时间 t 求导数并代入式(8)得
将牵连点 {M}_{1} 的矢径坐标 [式(18)] 对时间求二阶导数,注意式中坐标 {x}^{\prime }\text{、}{y}^{\prime }\text{、}{z}^{\prime } 均为常数得到牵连点加速度的表达式为
下面求动点牵连速度对时间的导数。由于动参考系上的牵连点随时间不断改变因此式 (19) 两端对时间求导数时${x}^{\prime }\text{、}{y}^{\prime }\text{、}{z}^{\prime }$ 不再是常数,由此得
其中 {x}^{\prime }\left( t\right) \text{、}{y}^{\prime }\left( t\right) 和 {z}^{\prime }\left( t\right) 反映了动参考系上的牵连点随时间的变化,而牵连点随时间的变化关系就是动点的相对运动方程。将式中等号右边第二项对时间的导数展开并代入式 (22)得
将式(21)和式(23)代入式(20),得到
令
表示相对运动与牵连运动的耦合作用,称为耦合加速度或科氏加速度。从而得到点合成运动分的加速度合成定理为析方法
即动点在某瞬时的绝对加速度等于该瞬时它的牵连加速度、相对加速度与科氏加速度的矢量和。
下面研究一下动参考系做两种简单运动时点的加速度合成定理的具体形式。
- 牵连运动是平移时点的加速度合成定理
设图 3 中动参考系 {O}^{\prime }{x}^{\prime }{y}^{\prime }{z}^{\prime } 做平移。由于 {x}^{\prime }\text{、}{y}^{\prime }\text{、}{z}^{\prime } 轴方向不变,故有
代入式(24),得到 {\mathbf{a}}_{\mathrm{c}} = \mathbf{0} ,式(25)可写成
上式表示:当牵连运动为平移时,动点在某瞬时的绝对加速度等于该瞬时它的相对加速度与牵连加速度的矢量和。
- 牵连运动是定轴转动时点的加速度合成定理
设图 3 中的动参考系做定轴转动,转轴通过点 {O}^{\prime } ,则有 {\mathbf{v}}_{{O}^{\prime }} = \mathbf{0} 。设其角速度矢量为 \mathbf{\omega } ,由例3 中的式 (24),动参考系的三个单位矢量 {\mathbf{i}}^{\prime }\text{、}{\mathbf{j}}^{\prime }\text{、}{\mathbf{k}}^{\prime } 对时间的导数为
代入式(19),得到
而
由牵连点的定义,对于任一瞬时 t ,动点与此瞬时的牵连点重合,从而有
牵连速度和牵连加速度的表达式可以写为
上两式与式(20)和式(21)一致。这里需要指出的是,虽然对瞬时 t 有 {\mathbf{r}}^{\prime } = {\mathbf{r}}_{1}^{\prime } 但是动点在不同瞬时的牵连点对应动参考系上不同的点。设 t + {\Delta t} 瞬时动点的牵连点为 {M}_{2} ,其在动参考系中的矢径为 {r}_{2}^{\prime } ,显然有
将 (27) 代入式 (24)得到
式(32)即为物理学中科氏加速度的标准表达式。
科氏加速度是由于动参考系为转动时牵连运动与相对运动相互影响而产生的。现通过一例给以形象说明。
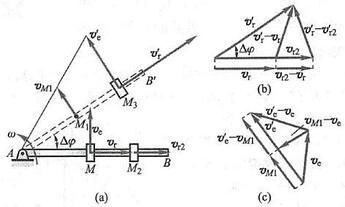
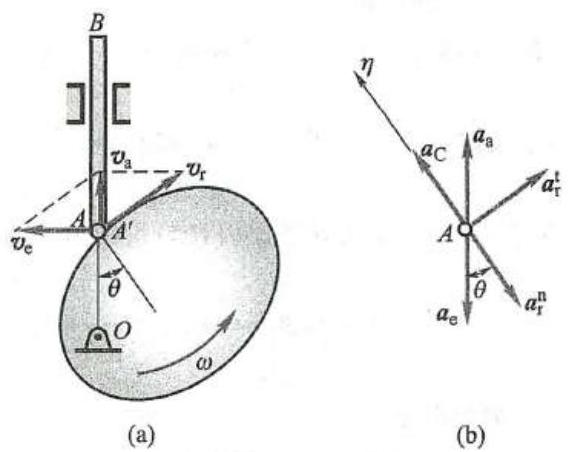
在图 13a 中,动点沿杆 {AB} 运动,而杆 {AB} 又绕 A 轴匀速转动。设动参考系固结在杆 {AB} 上。在瞬时 t ,动点在点 M 处,它的相对速度和牵连速度分别为 {v}_{\mathrm{r}} 和 {v}_{n} 。经过时间间隔 {\Delta t} 后,杆 {AB} 转到位置 A{B}^{\prime } ,动点移动到点 {M}_{3} ,这时它的相对速度为 {v}_{\mathrm{r}}^{\prime } ,牵连速度为 {v}_{\mathrm{e}}^{\prime } 。
图 13
如果杆 {AB} 不转动,则 t + {\Delta t} 时刻动点的相对速度是图中的 {v}_{\mathrm{r}2} ;由于牵连运动是转动,使 t + {\Delta t} 时刻动点的相对速度的方向又发生变化,变为图中的 {v}_{\mathrm{r}}^{\prime } 。相对加速度是在动参考系 {AB} 上观察的,只反映出由 {v}_{\mathrm{r}} 到 {v}_{\mathrm{r}2} 的速度变化,而由 {v}_{\mathrm{r}2} 变为 {v}_{\mathrm{r}}^{\prime } 则反映为科氏加速度的一部分 (图 13b)。
如果没有相对运动,则 t + {\Delta t} 时刻点 M 移到点 {M}_{1} ,牵连速度应为图中的 {v}_{M1} ;由于有相对运动,使 t + {\Delta t} 时刻的牵连速度不同于 {v}_{M1} 而变为图中的 {v}_{\mathrm{e}}^{\prime } 。牵连加速度是动参考系上点 M 的加速度,只反映出由 {v}_{\mathrm{e}} 到 {v}_{M1} 的速度变化,而由 {v}_{M1} 变为 {v}_{\mathrm{e}}^{\prime } ,则反映为科氏加速度的另一部分 (图 13c)。
上面的分析表明 (图 13):
科氏加速度 {a}_{\mathrm{c}} 正是由此产生的。下面两个等式读者可自行证明:
科氏加速度是 1832 年由科里奥利发现的,因而命名为科里奥利加速度,简称科氏加速度。科氏加速度在自然现象中是有所表现的。
地球绕地轴转动地球上物体相对于地球运动这都是牵连运动为转动的合成运动。地球自转角速度很小一般情况下其自转的影响可略去不计;但是在某些情况下,却必须给予考虑。
图 14
例如在北半球河水向北流动时河水的科氏加速度 {\mathbf{a}}_{\mathrm{c}} 向西,即指向左侧,如图 14 所示。由动力学可知有向左的加速度河水必受有右岸对水的向左的作用力。根据作用与反作用定律河水必对右岸有反作用力。北半球的江河其右岸都受有较明显的冲刷这是地理学中的一项规律。
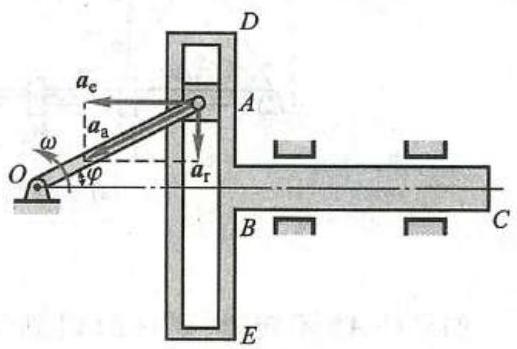
例 8 曲柄 {OA} 绕固定轴 O 转动,丁字形杆 {BC} 沿水平方向往复平移,如图 15 所示。铰接在曲柄 {OA} 端 A 的滑块可在丁字形杆 {BC} 的铅垂槽 {DE} 内滑动。设曲柄 {OA} 以角速度 \omega 做匀速转动${OA} = r$ ,试求丁字形杆 {BC} 的加速度。
图 15
解: 因丁字形杆 {BC} 做平移,故丁字形杆 {BC} 及铅垂槽 {DE} 上所有各点的加速度完全相同。显然,只要求出该瞬时铅垂槽 {DE} 上与曲柄 {OA} 端 A 相重合的那一点的加速度即可。
选取曲柄 {OA} 端 A 作为研究的动点,动参考系固定在丁字形杆 {BC} 上,于是动参考系做平移,可以应用点的加速度合成定理式 (26)。
动点 A 的绝对运动是以点 O 为圆心的圆周运动,因曲柄 {OA} 做匀速转动,故动点 A 的绝对加速度 {a}_{\mathrm{n}} 只有法向分量,大小为 r{\omega }^{2} ,方向由点 A 指向点 O;相对运动为沿槽 {DE} 的直线运动,相对加速度 {a}_{\mathrm{r}} 的方向沿铅垂槽 {DE} ;因动参考系做平移,各点轨迹为水平直线,故牵连加速度 {a}_{0} 沿水平方向。共有四个要素是已知的,可做出加速度平行四边形如图 15 所示。由图中三角关系求得
{a}_{\mathrm{e}} = {a}_{\mathrm{n}}\cos \varphi = r{\omega }^{2}\cos \varphi这就是丁字形杆 {BC} 的加速度。
例 9 图 16a 所示平面机构中,曲柄 {OA} 的长为 r ,以匀角速度 {\omega }_{0} 转动。套筒 A 可沿杆 {BC} 滑动。已知 {BC} = {DE} ,且 {BD} = {CE} = l 。求图示位置时,杆 {BD} 的角速度和角加速度。
图 16
解: 由于 {DBCE} 为平行四边形,因而杆 {BC} 做平移。以套筒 A 为动点,绝对速度 {v}_{\mathrm{a}} = r{\omega }_{0} 。以杆 {BC} 为动参考系,牵连速度 {v}_{\mathrm{e}} 等于点 B 速度 {v}_{B} 。其速度合成关系如图 16a 所示。 由图示几何关系解出
{v}_{\mathrm{e}} = {v}_{\mathrm{r}} = {v}_{\mathrm{n}} = r{\omega }_{0}因而杆 {BD} 的角速度 \omega 方向如图 16a 所示,大小为
\omega = \frac{{v}_{B}}{l} = \frac{{v}_{\mathrm{e}}}{l} = \frac{r{\omega }_{0}}{l} \tag{a}动参考系杆 {BC} 为曲线平移,牵连加速度与点 B 加速度相同,应分解为 {a}_{\mathrm{e}}^{\mathrm{t}} 和 {a}_{\mathrm{e}}^{\mathrm{n}} 两项。由点的加速度合成定理有
{a}_{\mathrm{u}} = {a}_{\mathrm{e}} + {a}_{\mathrm{r}} = {a}_{\mathrm{e}}^{\mathrm{t}} + {a}_{\mathrm{e}}^{\mathrm{n}} + {a}_{\mathrm{r}} \tag{b}其中
{a}_{\mathrm{a}} = {\omega }_{0}^{2}r,\;{a}_{\mathrm{e}}^{\mathrm{n}} = {\omega }^{2}l = \frac{{\omega }_{0}^{2}{r}^{2}}{l}而 {a}_{\mathrm{e}}^{\mathrm{t}} 和 {a}_{\mathrm{r}} 为未知量,暂设 {a}_{\mathrm{e}}^{\mathrm{t}} 和 {a}_{\mathrm{r}} 的指向如图 16b 所示。
将式 (b) 向 y 轴投影,得
{a}_{\mathrm{n}}\sin {30}^{ \circ } = {a}_{\mathrm{e}}^{\mathrm{t}}\cos {30}^{ \circ } - {a}_{\mathrm{e}}^{\mathrm{n}}\sin {30}^{ \circ }解出
{a}_{\mathrm{e}}^{\mathrm{t}} = \frac{\left( {{a}_{\mathrm{a}} + {a}_{\mathrm{e}}^{\mathrm{n}}}\right) \sin {30}^{ \circ }}{\cos {30}^{ \circ }} = \frac{\sqrt{3}{\omega }_{0}^{2}r\left( {l + r}\right) }{3l}解得 {a}_{\mathrm{e}}^{\mathrm{t}} 为正,表明所设 {a}_{\mathrm{e}}^{\mathrm{t}} 指向正确。
动参考系做平移,点 B 的加速度等于牵连加速度,因而杆 {BD} 的角加速度方向如图 16a 所示其值为
\alpha = \frac{{a}_{\mathrm{e}}^{\mathrm{t}}}{l} = \frac{\sqrt{3}{\omega }_{0}^{2}r\left( {l + r}\right) }{3{l}^{2}}
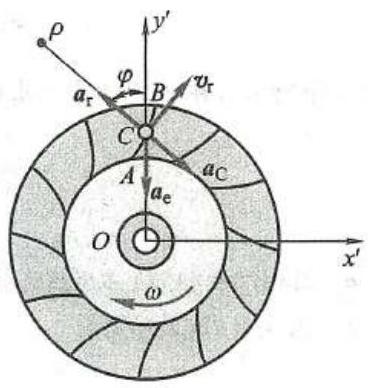
例 10 空气压缩机的工作轮以角速度 \omega 绕垂直于图面的 O 轴匀速转动,空气以相对速度 v ,沿弯曲的叶片匀速流动,如图 17 所示。如曲线 {AB} 在点 C 的曲率半径为 \rho ,通过点 C 的法线与半径间的夹角为 \varphi ,{CO} = r ,求气体微团在点 C 的绝对加速度 {a}_{\mathrm{a}} 。
解: 取气体微团为动点动参考系固定在工作轮上定参考系固定于地面。因动参考系做转动,故气体微团在点 C 的绝对加速度为相对加速度、牵连加速度和科氏加速度三项的合成。现分别求这三项加速度。
图 17
{a}_{\mathrm{e}} : 等于动参考系上的点 C 的加速度。因工作轮匀速转动,故只有向心加速度,即
{a}_{\mathrm{e}} = {\omega }^{2}r方向如图所示。
{\mathbf{a}}_{\mathrm{r}} : 由于气体微团相对于叶片做匀速曲线运动,故只有法向加速度即
{a}_{\mathrm{r}} = \frac{{v}_{\mathrm{r}}^{2}}{\rho }方向如图所示。
{\mathbf{a}}_{\mathrm{c}} : 由 {\mathbf{a}}_{\mathrm{c}} = 2{\mathbf{\omega }}_{\mathrm{e}} \times {\mathbf{v}}_{\mathrm{r}} 可确定 {\mathbf{a}}_{\mathrm{c}} 在图示平面内,并与 {\mathbf{v}}_{\mathrm{r}} 垂直,指向如图所示。它的大小为
{a}_{\mathrm{c}} = {2\omega }{v}_{\mathrm{r}}\sin {90}^{ \circ } = {2\omega }{v}_{\mathrm{r}}根据点的加速度合成定理:
{a}_{\mathrm{a}} = {a}_{\mathrm{e}} + {a}_{\mathrm{r}} + {a}_{\mathrm{C}}将其分别投影到 {x}^{\prime } 轴及 {y}^{\prime } 轴上,得
{a}_{a{x}^{\prime }} = {a}_{a{x}^{\prime }} + {a}_{r{x}^{\prime }} + {a}_{C{x}^{\prime }} = 0 - \frac{{v}_{r}^{2}}{\rho }\sin \varphi + {2\omega }{v}_{r}\sin \varphi = \left( {{2\omega }{v}_{r} - \frac{{v}_{r}^{2}}{\rho }}\right) \sin \varphi{a}_{a{y}^{\prime }} = {a}_{c{y}^{\prime }} + {a}_{c{y}^{\prime }} + {a}_{C{y}^{\prime }} = - r{\omega }^{2} + \frac{{v}_{r}^{2}}{\rho }\cos \varphi - {2\omega }{v}_{r}\cos \varphi = \left( {\frac{{v}_{r}^{2}}{\rho } - {2\omega }{v}_{r}}\right) \cos \varphi - r{\omega }^{2}于是绝对加速度的大小可按下式求得
{a}_{\mathrm{a}} = \sqrt{{a}_{\mathrm{a}{x}^{\prime }}^{2} + {a}_{\mathrm{a}{y}^{\prime }}^{2}}{\mathbf{a}}_{\mathrm{a}} 的方向可由其方向余弦确定。
例 11 求例 4 中摇杆 {O}_{1}B 在图 18 所示位置时的角加速度。
解:动点和动参考系选择同例 4。因为动参考系做转动,因此点的加速度合成定理为
{a}_{\mathrm{n}} = {a}_{\mathrm{e}} + {a}_{\mathrm{r}} + {a}_{\mathrm{C}}图 18
由于 {a}_{\mathrm{e}}^{1} = \alpha \cdot {O}_{1}A ,欲求摇杆 {O}_{1}B 的角加速度 \alpha ,只需求出 {a}_{\mathrm{e}}^{1} 即可。
现在分别分析上式中的各项。
{\mathbf{a}}_{\mathrm{n}} : 因为动点的绝对运动是以点 O 为圆心的匀速圆周运动,故只有法向加速度方向如图所示大小为
{a}_{n} = r{\omega }^{2}{\mathbf{a}}_{\mathrm{e}} : 摇杆 {O}_{1}B 上与动点相重合的那一点的加速度。摇杆 {O}_{1}B 摆动其上点 A 的切向加速度 {a}_{0}^{1} 垂直于杆 {O}_{1}A ,假设指向如图所示;法向加速度为 {\mathbf{a}}_{\mathrm{e}}^{\mathrm{n}} ,它的大小为
{a}_{\mathrm{e}}^{\mathrm{n}} = {\omega }_{1}^{2} \cdot {O}_{1}A方向如图所示。在例 4 中已求得 {\omega }_{1} = \frac{{r}^{2}\omega }{{l}^{2} + {r}^{2}} ,且 {O}_{1}A = \sqrt{{l}^{2} + {r}^{2}} ,故有
{a}_{\mathrm{e}}^{\mathrm{n}} = \frac{{r}^{4}{\omega }^{2}}{{\left( {l}^{2} + {r}^{2}\right) }^{3/2}}{\mathbf{a}}_{\mathrm{r}} : 因相对运动轨迹为直线,故 {\mathbf{a}}_{\mathrm{r}} 沿杆 {O}_{1}A ,大小未知。
{\mathbf{a}}_{\mathrm{c}} : 由 {\mathbf{a}}_{\mathrm{c}} = 2{\mathbf{\omega }}_{\mathrm{e}} \times {\mathbf{v}}_{\mathrm{r}} 知
{a}_{\mathrm{c}} = 2{\omega }_{1}{v}_{\mathrm{r}}\sin {90}^{ \circ }由例 4 知
{v}_{\mathrm{r}} = {v}_{\mathrm{a}}\cos \varphi = \frac{\omega rl}{\sqrt{{l}^{2} + {r}^{2}}}于是有
{a}_{\mathrm{C}} = \frac{2{\omega }^{2}{r}^{3}l}{{\left( {l}^{2} + {r}^{2}\right) }^{3/2}}方向如图所示。
为了求得 {\mathbf{a}}_{\mathrm{e}}^{\mathrm{t}} ,应将点的加速度合成定理公式向 {x}^{\prime } 轴投影,即
{a}_{a{x}^{\prime }} = {a}_{e{x}^{\prime }} + {a}_{t{x}^{\prime }} + {a}_{C{x}^{\prime }}或
- {a}_{\mathrm{n}}\cos \varphi = {a}_{\mathrm{n}}^{\prime } - {a}_{\mathrm{C}}解得
{a}_{\mathrm{e}}^{\mathrm{t}} = - \frac{{rl}\left( {{l}^{2} - {r}^{2}}\right) }{{\left( {l}^{2} + {r}^{2}\right) }^{3/2}}{\omega }^{2}式中 {l}^{2} - {r}^{2} > 0 ,故 {a}_{\mathrm{e}}^{\mathrm{t}} 为负值。负号表示 {a}_{\mathrm{e}}^{\mathrm{t}} 的真实方向与图中假设的指向相反。
杆 {O}_{1}A 的角加速度为
\alpha = \frac{{a}_{\mathrm{e}}^{\mathrm{t}}}{{O}_{1}A} = - \frac{{rl}\left( {{l}^{2} - {r}^{2}}\right) }{{\left( {l}^{2} + {r}^{2}\right) }^{2}}{\omega }^{2}负号表示角加速度 \alpha 的真实转向与图示方向相反,应为逆时针转向。
例 12 图 19a 所示凸轮机构中,凸轮以匀角速度 \omega 绕水平 O 轴转动,带动杆 {AB} 沿铅垂线上、下运动,且点 O\text{、}A\text{、}B 共线。凸轮上与点 A 接触的点为 {A}^{\prime } ,图示瞬时凸轮轮缘线上点 {A}^{\prime } 的曲率半径为 {\rho }_{A} ,点 {A}^{\prime } 的法线与 {OA} 夹角为 \theta ,{OA} = l 。求该瞬时杆 {AB} 的速度及加速度。
解: 如果取凸轮上点 {A}^{\prime } 作为动点,动参考系固结在杆 {AB} 上,所看到的相对运动轨迹是不清楚的。因此取杆 {AB} 上的点 A 为动点,动参考系固结在凸轮上。绝对运动是点 A 的直线运动,牵连运动是凸轮绕 O 轴的定轴转动,相对运动是点 A 沿凸轮轮缘的运动。各速度方向很容易画出,如图 19a 所示。由点的速度合成定理,有
{v}_{\mathrm{a}} = {v}_{\mathrm{e}} + {v}_{\mathrm{r}}图 19
其中 {v}_{\mathrm{e}} = {\omega l} ,可求得
{v}_{\mathrm{a}} = {\omega l}\tan \theta ,\;{v}_{\mathrm{r}} = {\omega l}/\cos \theta绝对运动是直线运动,因此 {a}_{\mathrm{a}} 沿直线 {AB} 方向;牵连运动是匀速定轴转动,因此 {a}_{\mathrm{e}} 指向点 O ;相对加速度由切向加速度 {\mathbf{a}}_{\mathrm{r}}^{\mathrm{t}} 及法向加速度 {\mathbf{a}}_{\mathrm{r}}^{\mathrm{n}} 两项组成。其中
{a}_{\mathrm{e}} = l{\omega }^{2},\;{a}_{\mathrm{r}}^{\mathrm{n}} = \frac{{v}_{\mathrm{r}}^{2}}{{\rho }_{A}} = \frac{{\omega }^{2}{l}^{2}}{{\rho }_{A}{\cos }^{2}\theta }由于牵连运动为匀速定轴转动,因此科氏加速度 {a}_{\mathrm{c}} 为
{\mathbf{a}}_{\mathrm{c}} = 2{\mathbf{\omega }}_{\mathrm{e}} \times {\mathbf{v}}_{\mathrm{r}}大小为
{a}_{\mathrm{c}} = {2\omega }{v}_{\mathrm{r}} = 2{\omega }^{2}l/\cos \theta各加速度方向如图 19b 所示。点的加速度合成定理为
{a}_{\mathrm{u}} = {a}_{\mathrm{c}} + {a}_{\mathrm{r}}^{\mathrm{t}} + {a}_{\mathrm{r}}^{\mathrm{n}} + {a}_{\mathrm{C}}在此矢量方程中,只有 {a}_{n} 的大小及 {a}_{r}^{\prime } 的大小未知。欲求 {a}_{n} ,可将此矢量方程向垂直于 {a}_{r}^{\prime } 的 \eta 轴上投影即
{a}_{\mathrm{a}}\cos \theta = - {a}_{\mathrm{e}}\cos \theta - {a}_{\mathrm{r}}^{\mathrm{n}} + {a}_{\mathrm{C}}解得
{a}_{\alpha } = - {\omega }^{2}l\left( {1 + \frac{l}{{\rho }_{A}{\cos }^{3}\theta } - \frac{2}{{\cos }^{2}\theta }}\right)
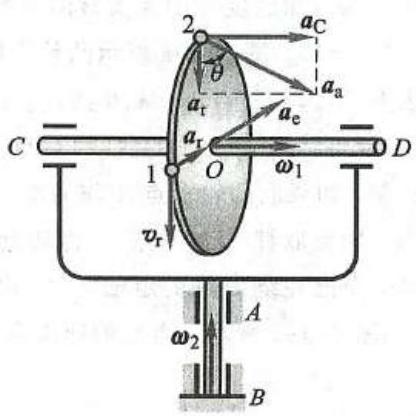
例 13 圆盘半径 R = {50}\mathrm{\;{mm}} ,以匀角速度 {\omega }_{1} 绕水平轴 {CD} 转动,同时框架和 {CD} 轴一起以匀角速度 {\omega }_{2} 绕通过圆盘中心 O 的铅垂轴 {AB} 转动,如图 20 所示。如 {\omega }_{1} = 5\mathrm{{rad}}/\mathrm{s},{\omega }_{2} = 3\mathrm{{rad}}/\mathrm{s} ,求圆盘上点 1 和点 2 的绝对加速度。
图 20
解: 首先计算点 1 的加速度。
取圆盘上的点 1 为动点动参考系与框架固结则动参考系绕 {AB} 轴转动。应用点的加速度合成定理,有
{a}_{\mathrm{a}} = {a}_{\mathrm{e}} + {a}_{\mathrm{r}} + {a}_{\mathrm{C}}{\mathbf{a}}_{\mathrm{e}} : 是动参考系上与动点相重合的那一点 (牵连点) 的加速度。动参考系为无限大其上与动点相重合的点以点 O 为圆心在水平面内做匀速圆周运动,因此该点只有法向加速度它的大小为
{a}_{\mathrm{e}} = {\omega }_{2}^{2}R = {\left( 3\mathrm{{rad}}/\mathrm{s}\right) }^{2} \times {50}\mathrm{\;{mm}} = {450}\mathrm{\;{mm}}/{\mathrm{s}}^{2}方向如图所示。
{\mathbf{a}}_{t} : 动点的相对运动以点 O 为圆心,在铅垂平面内做匀速圆周运动,因此也只有法向加速度它的大小为
{a}_{\mathrm{r}} = {\omega }_{1}^{2}R = {\left( 5\mathrm{{rad}}/\mathrm{s}\right) }^{2} \times {50}\mathrm{\;{mm}} = {1250}\mathrm{\;{mm}}/{\mathrm{s}}^{2}方向如图所示。
{\mathbf{a}}_{\mathrm{c}} : 由 {\mathbf{a}}_{\mathrm{c}} = 2{\mathbf{\omega }}_{\mathrm{e}} \times {\mathbf{v}}_{\mathrm{r}} 确定 {\mathbf{a}}_{\mathrm{c}} 的大小为
{a}_{\mathrm{c}} = 2{\omega }_{2}{v}_{\mathrm{r}}\sin {180}^{ \circ } = 0于是点 1 的绝对加速度的大小为
{a}_{\mathrm{a}} = {a}_{\mathrm{e}} + {a}_{\mathrm{r}} = {1700}\mathrm{\;{mm}}/{\mathrm{s}}^{2}它的方向与 {a}_{\mathrm{e}}\text{、}{a}_{\mathrm{r}} 的同向,指向轮心 O 。
现在计算点 2 的加速度。仍将动参考系固结在框架上。
{a}_{\mathrm{e}} : 因动参考系上与点 2 相重合的点是轴线上的一个点,该点的加速度等于零,因此 {a}_{\mathrm{e}} = 0 。
{\mathbf{a}}_{\mathrm{r}} : 相对加速度的大小为
{a}_{\mathrm{r}} = R{\omega }_{1}^{2} = {50}\mathrm{\;{mm}} \times {\left( 5\mathrm{{rad}}/\mathrm{s}\right) }^{2} = {1250}\mathrm{\;{mm}}/{\mathrm{s}}^{2}方向指向轮心 O 。
{a}_{\mathrm{c}} :
{a}_{\mathrm{c}} = 2{\omega }_{\mathrm{e}}{v}_{\mathrm{r}}\sin {90}^{ \circ } = 2{\omega }_{2}{\omega }_{1}R = 2 \times \left( {3\mathrm{{rad}}/\mathrm{s}}\right) \times \left( {5\mathrm{{rad}}/\mathrm{s}}\right) \times {50}\mathrm{\;{mm}}= {1500}\mathrm{\;{mm}}/{\mathrm{s}}^{2}{\mathbf{a}}_{\mathrm{c}} 垂直于圆盘平面,方向如图所示。
于是,点 2 的绝对加速度的大小为
{a}_{\mathrm{n}} = \sqrt{{a}_{\mathrm{r}}^{2} + {a}_{\mathrm{C}}^{2}} = {1953}\mathrm{\;{mm}}/{\mathrm{s}}^{2}它与铅垂线形成的夹角为
\theta = \arctan \frac{{a}_{\mathrm{C}}}{{a}_{\mathrm{r}}} = {50}^{ \circ }{12}^{\prime }
总结以上各例的解题步骤,可见应用加速度合成定理求解点的加速度其步骤基本上与应用速度合成定理求解点的速度相同但要注意以下几点:
(1)选取动点和动参考系后,应根据动参考系有无转动,确定是否有科氏加速度。
(2)因为点的绝对运动轨迹和相对运动轨迹可能都是曲线,因此点的加速度合成定理一般可写成如下形式:
式中每一项都有大小和方向两个要素,必须认真分析每一项,才可能正确地解决问题。
在平面问题中一个矢量方程相当于两个代数方程因而可求解两个未知量。上式中各项法向加速度的方向总是指向相应曲线的曲率中心它们的大小总是可以根据相应的速度大小和曲率半径求出。因此在应用加速度合成定理时,一般应先进行速度分析,这样各项法向加速度都是已知量。
科氏加速度 {a}_{\mathrm{c}} 的大小和方向由牵连角速度 {\omega }_{\mathrm{e}} 和相对速度 {v}_{\mathrm{r}} 确定,它们也完全可通过速度分析求出,因此 {a}_{\mathrm{c}} 的大小和方向两个要素也是已知的。这样在点的加速度合成定理中只有三项切向加速度的六个要素可能是待求量若知其中的四个要素则余下的两个要素就完全可求了。
在应用点的加速度合成定理时,正确选取动点和动参考系是很重要的。动点相对于动参考系是运动的因此它们不能处于同一刚体上。选择动点、动参考系时还要注意相对运动轨迹是否清楚。若相对运动轨迹不清楚,则相对加速度 {\mathbf{a}}_{\mathrm{r}}^{\mathrm{t}},{\mathbf{a}}_{\mathrm{r}}^{\mathrm{n}} 的方向就难以确定从而使待求量个数增加致使求解困难。