在讨论物体受力分析和平衡问题时,忽略了摩擦的影响,把物体之间的接触都看作是光滑的,这是在摩擦力不起重要作用的情况下而做的一种简化。
这样处理可使计算简单,并且一般情况下所得到的结果也能被工程实际所接受。但并不是在所有的情况下都可以忽略摩擦的影响。例如,重力水坝依靠摩擦力来防止坝体的滑动,带传动也依靠摩擦等。
按照接触物体之间相对运动的情况,摩擦可分为滑动摩擦与滚动摩擦。当两物体接触处有相对滑动或有相对滑动趋势时,在接触处的公切面内所受到的阻碍称为滑动摩擦。当两相互接触物体有相对滚动或相对滚动趋势时, 物体间产生的对滚动的阻碍称为滚动摩擦。
1 滑动摩擦
两个相互接触,表面粗糙的物体有相对滑动趋势或产生相对滑动时,在接触处的公切面内有一种阻碍现象发生,此种现象称为滑动摩擦,彼此间作用的阻碍相对滑动的阻力, 称为滑动摩擦力。前者称为静滑动摩擦, 对应的摩擦力为静滑动摩擦力 (简称静摩擦力),常以 {F}_{\mathrm{a}} 表示;后者称为动滑动摩擦,对应的摩擦力为动滑动摩擦力 (简称动摩擦力),常以 {\mathbf{F}}_{\mathrm{d}} 表示。
1.1 静摩擦力和静滑动摩擦定律
对滑动摩擦一般建立在如下简单实验的基础上,在水平平面上放一重量为 P 的物块,然后用一根重量可以不计的细绳跨过一小滑轮,绳的一端系在物块上, 另一端悬挂一可放砝码的平盘, 如图 1 所示。显然,当物块平衡时,绳对物块的拉力大小 {F}_{\mathrm{T}} 等于平盘与砝码的重量。当 {F}_{\mathrm{T}} 等于零时,物块处于静止状态,当 {F}_{\mathrm{T}} 逐渐增大 (盘中砝码增加)时,物块仍可处于静止状态。但当 {F}_{\mathrm{T}} 增大到某值时,物块将开始运动, 此时已为动滑动摩擦。现研究静滑动摩擦。取静止时的物块为研究对象,其受力图如图 1 所示, 由平衡方程
图 1
得 {F}_{\mathrm{s}} = {F}_{\mathrm{T}} 。由此可得静摩擦力的几个特点:
(1)方向 静摩擦力沿着接触处的公切线,与相对滑动趋势反向。
(2)大小 静摩擦力有一取值范围,为
{F}_{\text{smax }} 称为临界静摩擦力或最大静摩擦力,为物体处于临界平衡状态时的摩擦力,超过此值, 物体将开始运动。
(3)临界静摩擦力是一个很重要的量,大量实验和实践表明, {F}_{\text{smax }} 的大小与物体接触处的正压力 (法向约束力) {F}_{\mathrm{N}} 成正比,即
一般称之为静滑动摩擦定律(或库仑摩擦定律),是法国科学家库仑在做了大量实验的基础上得出的结论。式中的 {f}_{\mathrm{s}} 称为静摩擦因数。 {f}_{\mathrm{s}} 是一个量纲一的量,需由实验来确定,它与接触物体的材料、接触处的粗糙程度、湿度、温度、润滑情况等因素有关。静摩擦因数的数值可在工程手册中查到, 表 1 列出了部分常用材料的摩擦因数,但这是在常规情况下的,若需要较准确的数值,可在具体条件下由实验测定。
表 1 部分常用材料的摩擦因数
| 材料名称 | 静摩擦因数 | 动摩擦因数 | ||
| 无润滑 | 有润滑 | 无润滑 | 有润滑 | |
| 钢-钢 | 0.15 | 0.1~0.2 | 0.15 | 0.05~0.1 |
| 钢-软钢 | 0.2 | 0.1~0.2 | ||
| 钢-铸铁 | 0.3 | 0.18 | 0.05 ~ 0.15 | |
| 钢-青铜 | 0.15 | 0.1~0.15 | 0.15 | 0.1~0.15 |
| 软钢-铸铁 | 0.2 | 0.18 | 0.05~0.15 | |
| 软钢-青铜 | 0.2 | 0.18 | 0.07 ~0.15 | |
| 铸铁-铸铁 | 0.18 | 0.15 | 0.07 ~0.12 | |
| 铸铁-青铜 | 0.15 ~0.2 | 0.07 ~0.15 | ||
| 青铜-青铜 | 0.1 | 0.2 | 0.07 ~0.1 | |
| 皮革-铸铁 | 0.3~0.5 | 0.15 | 0.6 | 0.15 |
| 橡皮-铸铁 | 0.8 | 0.5 | ||
| 木材-木材 | 0.4~0.6 | 0.1 | 0.2~0.5 | 0.07 ~0.15 |
1.2 动摩擦力
当静摩擦力已达到最大值时,若主动力 \mathbf{F} 再继续加大,则接触面之间将出现相对滑动。此时,接触物体之间仍作用有阻碍相对滑动的阻力, 这种阻力称为动滑动摩擦力,简称动摩擦力,以 {F}_{\mathrm{d}} 表示。实验表明:动摩擦力的大小与接触物体间的正压力成正比,即
式中,f 是动摩擦因数,它与接触物体的材料和表面情况有关。
一般情况下,动摩擦因数小于静摩擦因数,即 f < {f}_{\mathrm{s}} 。
实际上动摩擦因数还与接触物体间相对滑动的速度大小有关。对于不同材料的物体,动摩擦因数随相对滑动的速度变化规律也不同。多数情况下,动摩擦因数随相对滑动速度的增大而稍减小。但当相对滑动速度不大时,可近似地认为动摩擦因数是个常数, 参阅表 1。
在机器中, 往往用降低接触表面的粗糙度或加入润滑剂等方法, 使动摩擦因数 f 降低,以减小摩擦和磨损。
2 摩擦角和自锁现象
2.1 全约束力与摩擦角
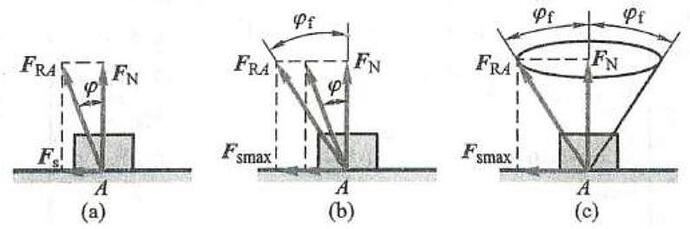
当有静滑动摩擦时,支承面对物体的约束力包含法向约束力 {\mathbf{F}}_{\mathrm{N}} 和切向约束力 {\mathbf{F}}_{\mathrm{s}} (即静摩擦力)。为讨论问题的方便,在某些情况下,把这两个力合起来,即 {\mathbf{F}}_{\mathrm{R}A} = {\mathbf{F}}_{\mathrm{N}} + {\mathbf{F}}_{\mathrm{s}} ,称之为全约束力。全约束力的作用线与接触处的公法线间有一夹角 \varphi ,如图 2a 所示。当物块处于临界平衡状态时,静摩擦力达到由式 (2) 确定的最大值,偏角 \varphi 也达到最大值 {\varphi }_{\mathrm{f}} ,如图 2b 所示。全约束力与法线间的夹角的最大值称为摩擦角。由图 2b 可得
即摩擦角的正切等于静摩擦因数。可见,摩擦角与摩擦因数一样,都是表示摩擦的一个重要物理量。
图 2
当物块的滑动趋势任意改变时,全约束力作用线的方位也随之任意改变。 {\mathbf{F}}_{\mathrm{R}A} 的作用线将画出一个以接触点为顶点的锥面。在临界状态下,如图 2c 所示,此时的锥体称为摩擦锥。若物块与支承面沿任何方向的摩擦因数都相同, 则摩擦锥是一个顶角为 2{\varphi }_{\mathrm{f}} 的圆锥。
2.2 自锁现象
物块平衡时,静摩擦力不一定达到最大值,在零与最大值 {F}_{\text{smax }} 之间变化,所以全约束力的作用线与法线间的夹角 \varphi 在零与摩擦角 {\varphi }_{\mathrm{f}} 之间变化,即
因为静摩擦力不能超过最大值 {F}_{\text{smax }} ,所以全约束力的作用线也不能超出摩擦角 (锥) 之外, 即全约束力的作用线必在摩擦角 (锥) 之内。由此可知:
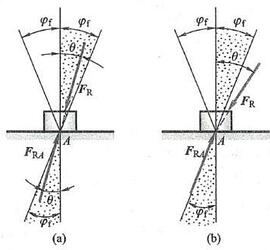
(1)如果作用在物体上的全部主动力的合力 {\mathbf{F}}_{\mathrm{R}} 的作用线在摩擦角 {\varphi }_{\mathrm{f}} 之内,且指向支承面,则无论这个力多么大,物体必保持静止,这种现象称为自锁现象。在这种情况下,主动力的合力 {\mathbf{F}}_{\mathrm{R}} 与法线间的夹角 \theta < {\varphi }_{\mathrm{f}} ,由二力平衡条件,全约束力 {\mathbf{F}}_{\mathrm{{RA}}} 可以和主动力的合力 {\mathbf{F}}_{\mathrm{R}} 等值、反向、共线,且和主动力的大小无关,如图 3a 所示。工程中常应用自锁条件设计一些机构或夹具, 如千斤顶、压榨机、圆锥销等,使它们始终保持在平衡状态下工作。
图 3
(2)如果全部主动力的合力 {\mathbf{F}}_{\mathrm{R}} 的作用线在摩擦角 {\varphi }_{\mathrm{f}} 之外,则无论这个力多么小, 物体一定会滑动。在这种情况下 \theta > {\varphi }_{\mathrm{f}} ,全约束力 {\mathbf{F}}_{\mathrm{{RA}}} 的作用线只有在摩擦角之外才可能与主动力的作用线共线,这是不可能的,如图 3b 所示。 应用这个道理, 可以设法避免自锁现象, 如各种传动机构。
2.3 摩擦角应用举例
(1)测定静摩擦因数的一种简易方法
图 4
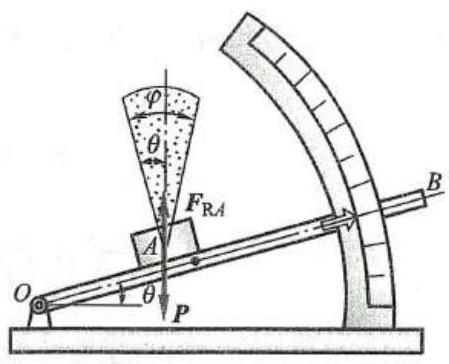
利用摩擦角的概念,可用简单的实验方法, 因时因地测定静摩擦因数。如图 4 所示, 把要测定静摩擦因数的同种材料或不同种材料分别做成板状与物块 (在能做成板状与物块的情况下),把物块放在板状物体上,使板的倾角从零 (水平位置) 开始逐渐增大至 \theta ,直到物块即将向下滑动时为止, 测出此时板的倾角 \theta ,则 \theta 就是物体间的摩擦角,其正切就是要测定的静摩擦因数 {f}_{\mathrm{s}} 。理由如下:由于物块仅受重力 \mathbf{P} 和全约束力 {\mathbf{F}}_{\mathrm{{RA}}} 作用而平衡,此两力必等值、反向、共线,则 {\mathbf{F}}_{\mathrm{{RA}}} 必沿铅垂线。当物块处于临界平衡状态时, 全约束力与板法线间的夹角为摩擦角, 而此角正好就是板的倾角。
(2)斜面与螺纹自锁条件
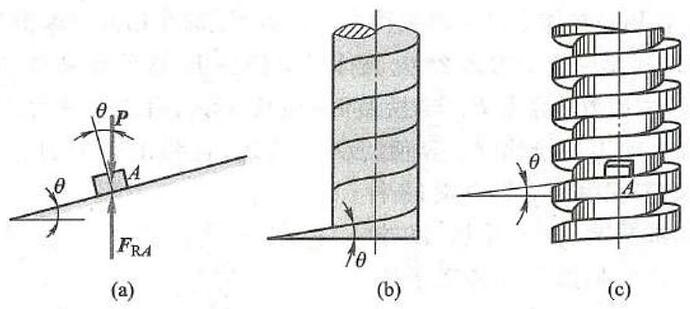
由上面测定静摩擦因数的方法知,物块在铅垂载荷 P 作用下沿斜面不下滑的条件是 \theta \leq {\varphi }_{1} ,这就是斜面的自锁条件,如图 5a 所示。即斜面自锁的条件是:斜面的倾角小于或等于材料的摩擦角。在交通领域修建各种坡路时, 车轮与路面间的摩擦因数是确定的, 因而摩擦角也是确定的值, 为保证各种车辆在坡路上因各种原因刹车而静止不动,对坡路的倾角就有一定的要求,这是斜面自锁的一个实例。
图 5
斜面的自锁条件也是螺旋 (图 5c) 的自锁条件,因为螺旋可以看做是绕在圆柱体上的斜面,如图 5b 所示,螺旋升角就是斜面的倾角,取微段考虑,螺母相当于物块 A ,加于螺母的轴向载荷相当于物块的重力。要使螺旋自锁,必须使螺旋的升角 \theta 小于或等于摩擦角 {\varphi }_{\mathrm{f}} ,螺旋的自锁条件和斜面的自锁条件相同。如螺旋千斤顶的螺杆与螺母间的静摩擦因数为 {f}_{\mathrm{s}} = {0.1} ,则 \tan {\varphi }_{\mathrm{f}} = {f}_{\mathrm{s}} = {0.1} ,得 {\varphi }_{\mathrm{f}} = {5}^{ \circ }{43}^{\prime } ,为保证螺旋千斤顶自锁,一般取螺纹升角 \theta = {4}^{ \circ } \sim {4}^{ \circ }{30}^{\prime } 。
堆放粮食、沙子、煤等颗粒状物体所形成的锥形的倾斜角度, 铁路、公路路基斜坡的角度, 自动卸货车翻斗抬起的角度等均可用自锁与非自锁的条件来讨论。同时, 在一些情况下, 用摩擦角求解平衡问题也比较方便。
3 考虑摩擦时物体的平衡问题
考虑滑动摩擦时,求解物体平衡问题的步骤与前几章基本相同,但有如下几个新特点:
(1)分析物体受力且画受力图时,必须考虑接触处沿切向的摩擦力。在滑动趋势 (或方向) 已知的情况下, 摩擦力应和滑动趋势 (或方向) 反向画出。在滑动趋势未知的情况下, 摩擦力的方向可以沿切线方位假设。因此时摩擦力为未知, 一般就增加了未知量的数目。
(2)严格区分物体是处于非临界平衡状态还是临界平衡状态。在非临界平衡状态,静摩擦力 {F}_{\mathrm{s}} 由平衡条件来确定,其应满足方程 {F}_{\mathrm{s}} < {f}_{\mathrm{s}}{F}_{\mathrm{N}} ; 在临界平衡状态,静摩擦力达到临界值,此时方可使用方程 {F}_{\mathrm{s}} = {F}_{\mathrm{s}\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}} 。
(3)由于静摩擦力 {F}_{\mathrm{s}} 的值可以随主动力而变化,即 0 \leq {F}_{\mathrm{s}} \leq {f}_{\mathrm{s}}{F}_{\mathrm{N}} ,因此在考虑摩擦的平衡问题中, 求出的值有时也有一个变化范围。
(4)考虑摩擦的平衡问题一般可分为两类:一类为在载荷或其他条件已知的情况下, 判断系统是否平衡的问题; 另一类为求系统处于平衡 (或非平衡) 状态所需满足的条件。第一类问题一般假设系统平衡, 此时的摩擦力为静摩擦力, 如果静摩擦力的方向不易判断, 也可以假设方向, 根据计算结果是否满足平衡条件 (静摩擦力不得大于最大静摩擦力、物体不得翻倒等)来判断系统是否平衡。第二类问题一般考虑临界平衡状态, 包括临界滑动和临界翻倒 (有时涉及) 等。临界滑动时的摩擦力对应的是最大静摩擦力,并且方向确定,求得的解为考虑临界滑动时的极限解, 也可以列不等式求解。临界翻倒时一般列力矩方程得到此时的极限解。将两种情况综合考虑得到系统应满足的条件。
下面举例说明考虑滑动摩擦时物体的平衡问题。
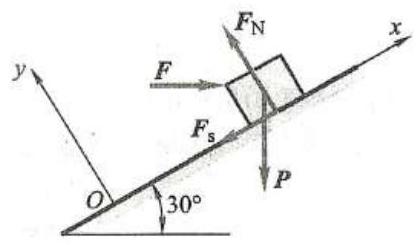
例 1 物块重 P = {1500}\mathrm{\;N} ,放于倾角为 {30}^{ \circ } 的斜面上,它与斜面间的静摩擦因数 {f}_{\mathrm{s}} = {0.2} ,动摩擦因数 f = {0.18} 。物块受水平力 F = {400}\mathrm{\;N} 作用,如图 6 所示。物块是否保持静止? 并求此时摩擦力的大小与方向。
图 6
解:物块是否静止未知,摩擦力大小和方向也未知,该问题属于第一类平衡问题。此题可以先假设物块静止, 假设静摩擦力方向,求出静摩擦力,与最大静摩擦力比较,可判定物块是否静止, 然后求出摩擦力。
取物块为研究对象,设静摩擦力沿斜面向下,物块平衡,受力如图 6 所示。在图示坐标系下列平衡方程:
\sum {F}_{x} = 0,\; - P\sin {30}^{ \circ } + F\cos {30}^{ \circ } - {F}_{\mathrm{s}} = 0\sum {F}_{y} = 0,\; - P\cos {30}^{ \circ } - F\sin {30}^{ \circ } + {F}_{\mathrm{N}} = 0把 P 与 F 的值代入,得静摩擦力与法向约束力分别为
{F}_{\mathrm{s}} = - {403.6}\mathrm{\;N},\;{F}_{\mathrm{N}} = {1499}\mathrm{\;N}静摩擦力为负值, 说明平衡时静摩擦力与所假设的方向相反, 即沿斜面向上。而最大静摩擦力为
{F}_{\mathrm{s}\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}} = {299.8}\mathrm{\;N}此计算表明,物块若平衡,静摩擦力大于最大静摩擦力,这是不可能的,物块不可能在斜面上静止, 而是向下滑动。因此, 此时的摩擦力应为动摩擦力, 方向沿斜面向上, 其大小为
{F}_{\mathrm{d}} = f{F}_{\mathrm{N}} = {269.8}\mathrm{\;N}
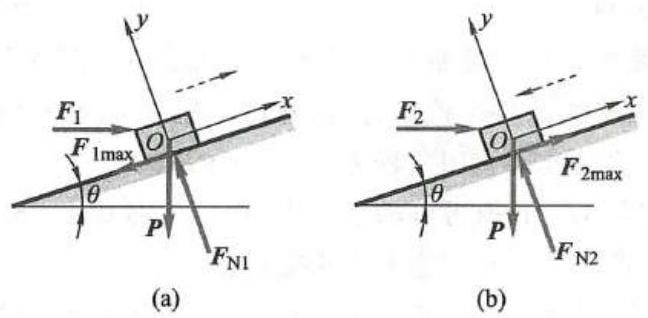
例 2 物体重为 P ,放在倾角为 \theta 的斜面上,与斜面间的静摩擦因数为 {f}_{\mathrm{s}} ,如图 7a 所示。 忽略物块的尺寸,当物体处于平衡状态时,求水平力 \mathbf{F} 的大小。
图 7
解:该问题属于第二类平衡问题。由经验知,当力 \mathbf{F} 大于某值时,物块将上滑; 当力 \mathbf{F} 小于某值时,物块将下滑。因此力 \mathbf{F} 的值在某一范围内,只需求出其两端的值,力 \mathbf{F} 的值在此之间即可。
设水平推力的大小为 {F}_{1} 时,物体处于将要向上滑动的临界状态,物体的受力图如图 7a 所示, 建立坐标系如图所示, 列平衡方程, 为
\sum {F}_{x} = 0,\;{F}_{1}\cos \theta - P\sin \theta - {F}_{1\max } = 0 \tag{1}\sum {F}_{y} = 0,\;{F}_{\mathrm{N}1} - {F}_{1}\sin \theta - P\cos \theta = 0 \tag{2}此时有
{F}_{1\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}1} \tag{3}联立求解 3 个方程, 得
{F}_{1} = \frac{\sin \theta + {f}_{\mathrm{s}}\cos \theta }{\cos \theta - {f}_{\mathrm{s}}\sin \theta }P设水平推力的大小为 {F}_{2} 时,物体处于将要向下滑动的临界状态,物体的受力图如图 7b 所示, 建立坐标系如图所示, 列平衡方程, 为
\sum {F}_{s} = 0,\;{F}_{2}\cos \theta - P\sin \theta + {F}_{2\max } = 0 \tag{4}\sum {F}_{y} = 0,\;{F}_{\mathrm{N}2} - {F}_{2}\sin \theta - P\cos \theta = 0 \tag{5}此时有
{F}_{2\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}2} \tag{6}联立求解 3 个方程, 得
{F}_{2} = \frac{\sin \theta - {f}_{\mathrm{s}}\cos \theta }{\cos \theta + {f}_{\mathrm{s}}\sin \theta }P则使物体静止时,水平推力 \mathbf{F} 的大小为
\frac{\sin \theta - {f}_{\mathrm{s}}\cos \theta }{\cos \theta + {f}_{\mathrm{s}}\sin \theta }P \leq F \leq \frac{\sin \theta + {f}_{\mathrm{s}}\cos \theta }{\cos \theta - {f}_{\mathrm{s}}\sin \theta }P此题如不计摩擦,即 {f}_{\mathrm{s}} = 0 ,平衡时应有 F = P\tan \theta ,其值是唯一的。
注意:在临界状态下求解有摩擦的平衡问题时,必须根据相对滑动的趋势,正确判定并画出摩擦力的方向,不能像例 1 一样任意假设。这是因为解题中引用了补充方程 {F}_{\text{smax }} = {f}_{\mathrm{s}}{F}_{\mathrm{N}} ,由于 {f}_{\mathrm{s}} 为正值, {F}_{\text{smax }} 与 {F}_{\mathrm{N}} 有相同的符号。法向约束力 {F}_{\mathrm{N}} 的方向总是确定的, {F}_{\mathrm{N}} 值为正,因而 {F}_{\text{smax }} 也始终为正值,这反映不出摩擦力的方向。所以 {\mathbf{F}}_{\text{smax }} 的方向不能假定,必须按真实方向画出。
此题也可用摩擦角概念,用几何法求解。
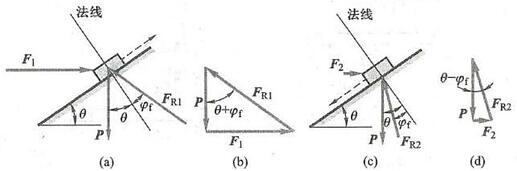
当水平推力的大小为 {F}_{1} 时,把摩擦力和法向约束力合起来考虑,画出受力图如图 8\mathrm{a} 所示。因为不计物块尺寸,可视为平面汇交力系,画出封闭力三角形如图 8b 所示,可直接解得
{F}_{1} = P\tan \left( {\theta + {\varphi }_{\mathrm{f}}}\right)图 8
当水平推力的大小为 {F}_{2} 时,把摩擦力和法向约束力合起来考虑,画出受力图如图 8c 所示,画出封闭力三角形如图 8d 所示,可直接解得
{F}_{2} = P\tan \left( {\theta - {\varphi }_{\mathrm{f}}}\right)则使物体静止时,水平推力 \mathbf{F} 的大小为
P\tan \left( {\theta - {\varphi }_{\mathrm{f}}}\right) \leq F \leq P\tan \left( {\theta + {\varphi }_{\mathrm{f}}}\right)按三角公式展开上式中的 \tan \left( {\theta - {\varphi }_{\mathrm{f}}}\right) 和 \tan \left( {\theta + {\varphi }_{\mathrm{f}}}\right) ,得
P\frac{\tan \theta - \tan {\varphi }_{\mathrm{f}}}{1 + \tan \theta \tan {\varphi }_{\mathrm{f}}} \leq F \leq P\frac{\tan \theta + \tan {\varphi }_{\mathrm{f}}}{1 - \tan \theta \tan {\varphi }_{\mathrm{f}}}由摩擦角定义, \tan {\varphi }_{\mathrm{f}} = {f}_{\mathrm{s}} ,代入上式,得
\frac{\sin \theta - {f}_{\mathrm{s}}\cos \theta }{\cos \theta + {f}_{\mathrm{s}}\sin \theta }P \leq F \leq \frac{\sin \theta + {f}_{\mathrm{s}}\cos \theta }{\cos \theta - {f}_{\mathrm{s}}\sin \theta }P结果完全相同。
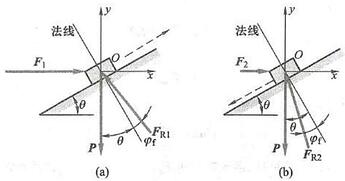
对图 8a、c,也可建立如图 9 所示坐标系列平衡方程,不画出封闭力三角形,用解析法求解, 求解略。
图 9
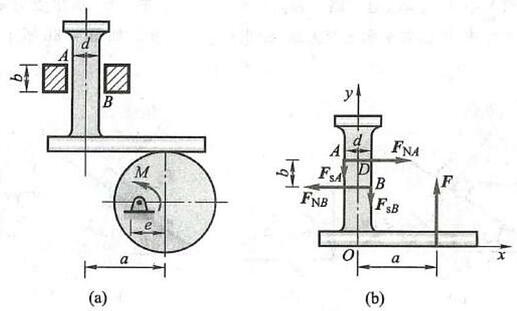
例 3 图 10a 所示为凸轮挺杆机构。已知不计自重的挺杆与滑道间的静摩擦因数为 {f}_{\mathrm{s}} ,滑道宽度为 b ,凸轮与挺杆接触处的摩擦忽略不计。问 a 为多大时,挺杆不至于被卡住?
图 10
解:此题属于第二类平衡问题。取挺杆为研究对象,其受力图如图 10b 所示,挺杆除受凸轮推力 \mathbf{F} 作用外,在滑道 A\text{、}B 处还受法向约束力 {\mathbf{F}}_{NA} 与 {\mathbf{F}}_{NB} 作用,由于挺杆有向上滑动趋势,静摩擦力 {\mathbf{F}}_{\mathrm{s}A} 与 {\mathbf{F}}_{\mathrm{s}B} 的方向向下。
列平衡方程
\sum {F}_{x} = 0,\;{F}_{NA} - {F}_{NB} = 0 \tag{a}\sum {F}_{y} = 0,\; - {F}_{sA} - {F}_{sB} + F = 0 \tag{b}\sum {M}_{D}\left( \mathbf{F}\right) ,\;{Fa} - {F}_{NB}b - {F}_{nB}\frac{d}{2} + {F}_{sA}\frac{d}{2} = 0 \tag{c}考虑平衡的临界情况 (即挺杆将动而尚未动时), A\text{、}B 处的静摩擦力都达到最大值,列出两个补充方程:
{F}_{nA} = {f}_{n}{F}_{NA} \tag{d}{F}_{\mathrm{s}B} = {f}_{\mathrm{s}}{F}_{\mathrm{N}B} \tag{e}由式 (a) 得
{F}_{NA} = {F}_{NB} = {F}_{N}代入式 (d) 和式 (e), 得
{F}_{\mathrm{s}A} = {F}_{\mathrm{s}B} = {F}_{\mathrm{s}\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}}代入式(b),得
F = 2{F}_{\text{smax }}最后代入式 (c),注意 {F}_{\mathrm{N}B} = {F}_{\text{smax }}/{f}_{\mathrm{s}} ,解得
{a}_{\text{极限 }} = \frac{b}{2{f}_{\mathrm{s}}}保持 F 和 b 不变,由式 (c) 可见,当 a 减小时, {F}_{NB}\left( { = {F}_{NA}}\right) 亦减小,因而最大静摩擦力减小,式 (b) 不成立,因而当 a < \frac{b}{2{f}_{a}} 时,挺杆不能平衡,即挺杆不会被卡住。
本题还可以用几何法求解。取挺杆为研究对象,将 A\text{、}B 处的摩擦力和法向力分别合成为全约束力 {\mathbf{F}}_{\mathrm{R}A} 和 {\mathbf{F}}_{\mathrm{R}B} 。于是,挺杆在 \mathbf{F}\text{、}{\mathbf{F}}_{\mathrm{R}A} 和 {\mathbf{F}}_{\mathrm{R}B} 三个力作用下平衡。
在图上画出挺杆的几何尺寸,并在 A\text{、}B 两点画出摩擦角 {\varphi }_{1} ,两直线交于点 C ,如图 11 所示,点 C 至挺杆中心线的距离即为所求的临界值 {a}_{\text{极限 }} ,计算得
{a}_{\text{极限 }} = \frac{b}{2}\cot {\varphi }_{\mathrm{f}} = \frac{b}{2{f}_{\mathrm{a}}}由摩擦力的性质可知, A\text{、}B 处的全约束力只能在摩擦角以内,也就是两个力的作用线的交点只可能在点 C 或点 C 的右侧 (阴影部分内)。根据三力平衡汇交定理, 只有 \mathbf{F}\text{、}{\mathbf{F}}_{\mathrm{R}A} 和 {\mathbf{F}}_{\mathrm{R}B} 三个力汇交于一点时推杆才能平衡。 由于 {\mathbf{F}}_{\mathrm{R}A} 和 {\mathbf{F}}_{\mathrm{R}B} 在点 C 左侧不可能相交,因此当 a < {a}_{\text{极限 }} 或 a < \frac{b}{2{f}_{\mathrm{s}}} 时,三个力不可能汇交,即推杆不能被卡住。而当 a \geq \frac{b}{2{f}_{\mathrm{s}}} 时,三个力将汇交于一点而平衡,此时无论推力 \mathbf{F} 多大也不能推动推杆,推杆将被卡住 (自锁)。
图 11
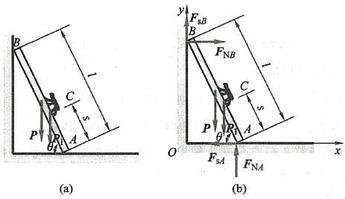
例 4 如图 12a 所示,梯子 {AB} 靠在墙上,其重量 P = {200}\mathrm{\;N} ,梯子长度为 l ,与水平面的夹角 \theta = {60}^{ \circ } 。已知梯子与地面和墙壁间的静摩擦因数 {f}_{\mathrm{s}} 均为 0.25。今有一重量为 {P}_{\mathrm{t}} = {650}\mathrm{\;N} 的人沿梯子上爬,求人能达到的最高点 C 到点 A 的距离 s ;若人能爬到顶点,则静摩擦因数至少需要多大?
图 12
解:此题属于考虑摩擦的第二类平衡问题。人越往上爬,其重力 {\mathbf{P}}_{1} 对点 A 的力矩越大,梯子越容易滑倒。当人到达能达到的最高点 C 时,梯子处于将要滑动的临界状态。取此临界状态进行分析,此时梯子的受力图如图 12b 所示。建立图示坐标系,列平衡方程,有
\sum {F}_{x} = 0,\;{F}_{NB} - {F}_{sA} = 0\sum {F}_{y} = 0,\;{F}_{\mathrm{N}A} + {F}_{\mathrm{s}B} - P - {P}_{1} = 0\sum {M}_{A} = 0,\;P \cdot \frac{l}{2}\cos {60}^{ \circ } + {P}_{1} \cdot s \cdot \cos {60}^{ \circ } - {F}_{\mathrm{N}B} \cdot l\sin {60}^{ \circ } - {F}_{\mathrm{s}B} \cdot l\cos {60}^{ \circ } = 0因为梯子处于临界状态,所以此时 A\text{、}B 两点对应的静摩擦力均为最大静摩擦力,补充库仑摩擦定律方程:
{F}_{\mathrm{s}A} = {f}_{\mathrm{s}}{F}_{\mathrm{N}A},\;{F}_{\mathrm{s}B} = {f}_{\mathrm{s}}{F}_{\mathrm{N}B}联立上述 5 个方程, 解得
s = \frac{l}{325}\left( {\frac{{425}\left( {\sqrt{3} + {f}_{\mathrm{s}}}\right) + 1}{{f}_{\mathrm{s}}} - {50}}\right) = {0.456l}因此,人能达到的最高点 C 到点 A 的距离 s = {0.456}{l}_{0}
若人能爬到顶点,则 s = l ,代入上式解得 {f}_{\mathrm{s}} = {0.433} ,即静摩擦因数至少为 0.433。此题若不计梯子重力, 则梯子仅受三个力的作用, 可用摩擦角来求解。
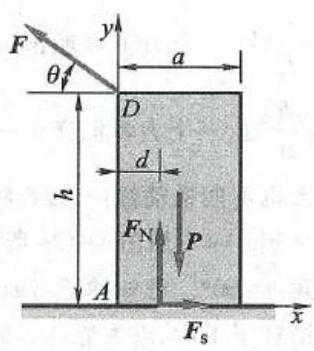
例 5 图 13 所示的均质木箱重 P = 5\mathrm{{kN}} ,与地面间的静摩擦因数 {f}_{\mathrm{s}} = {0.4} 。图中 h = {2a} = 2\mathrm{\;m},\theta = {30}^{ \circ } 。(1)当 D 处的拉力 F = 1\mathrm{{kN}} 时,木箱是否平衡?(2)求能保持木箱平衡的最大拉力。
解:此例涉及两类平衡问题,且需考虑翻倒情况。欲保持木箱平衡,必须满足两个条件:一是木箱不发生滑动,即要求静摩擦力 {F}_{\mathrm{a}} \leq {F}_{\max } = {f}_{\mathrm{a}}{F}_{\mathrm{N}} ;二是木箱不绕点 A 翻倒,这时法向力 {F}_{\mathrm{N}} 的作用线应在木箱内,即 d > 0 。
图 13
(1) 取木箱为研究对象, 受力图如图 13 所示, 列平衡方程:
\sum {F}_{x} = 0,\;{F}_{s} - F\cos \theta = 0 \tag{a}\sum {F}_{y} = 0,\;{F}_{N} - P + F\sin \theta = 0 \tag{b}\sum {M}_{A}\left( F\right) = 0,\;F\cos \theta \cdot h - P \cdot \frac{a}{2} + {F}_{\mathrm{N}} \cdot d = 0 \tag{c}求解以上方程, 得
{F}_{\mathrm{s}} = {0.866}\mathrm{{kN}},\;{F}_{\mathrm{N}} = {4.5}\mathrm{{kN}},\;d = {0.171}\mathrm{\;m}此时木箱与地面间的最大静摩擦力
{F}_{\max } = {f}_{\mathrm{s}}{F}_{\mathrm{N}} = {1.8}\mathrm{{kN}}可见, {F}_{\mathrm{a}} < {F}_{\text{smax }} ,木箱不滑动; 又 d > 0 ,木箱不会翻倒。因此,木箱保持平衡。
(2)为求保持平衡的最大拉力 F ,可分别求出木箱将滑动时的临界拉力 {F}_{\text{闭}} 和木箱将绕点 A 翻倒的临界拉力 {F}_{\text{翻 }} 。二者中取其较小者,即为所求。
木箱将滑动的条件为
{F}_{\mathrm{s}} = {F}_{\mathrm{{smax}}} = {f}_{\mathrm{s}}{F}_{\mathrm{N}} \tag{d}联立式 (a) 、式 (b) 、式 (d) 解得
{F}_{\text{损 }} = \frac{{f}_{\mathrm{s}}P}{\cos \theta + {f}_{\mathrm{s}}\sin \theta } = {1.876}\mathrm{{kN}}木箱将绕点 A 翻倒的条件为 d = 0 ,代入式 (c),得
{F}_{\text{磁 }} = \frac{Pa}{{2h}\cos \theta } = {1.443}\mathrm{{kN}}因为 {F}_{\text{群 }} < {F}_{\text{群 }} ,所以保持木箱平衡的最大拉力为
F = {F}_{\text{闭}} = {1.443}\mathrm{{kN}}这说明,当拉力 F 逐渐增大时,木箱将先翻倒而失去平衡。
4 滚动摩擦的概念
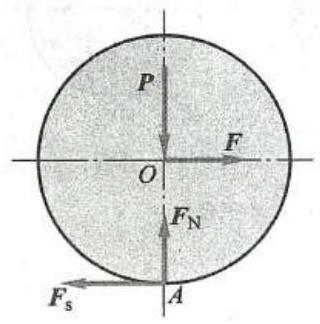
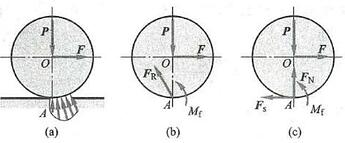
由实践可知,使滚子滚动比使它滑动省力。所以在工程中,为了提高效率,减轻劳动强度,常利用物体的滚动代替物体的滑动。当物体滚动时,存在什么阻力? 它有什么特性? 下面通过简单的实例来分析这些问题。设在水平面上有一滚子, 重量为 P ,半径为 r ,在其中心 O 上作用一水平力 F ,如图 14 所示。当力 F 不大时,滚子仍保持静止。分析滚子的受力情况可知,在滚子与平面的接触点 A 有法向约束力 {\mathbf{F}}_{\mathrm{N}} ,它与 \mathbf{P} 等值反向。另外,还有静摩擦力 {\mathbf{F}}_{\mathrm{s}} 阻止滚子滑动,它与 \mathbf{F} 等值反向。则图 14 所示滚子不可能保持平衡,因为静摩擦力 {\mathbf{F}}_{\mathrm{s}} 与力 \mathbf{F} 组成一力偶, 将使滚子发生滚动。但是,实际上当力 \mathbf{F} 不大时,滚子是可以平衡的。这是因为滚子和平面实际上并不是刚体,它们在力的作用下都会发生变形,有一个接触面,如图 15a 所示。在接触面上,物体受分布力的作用,这些力向点 A 简化,得到一个力 {\mathbf{F}}_{\mathrm{R}} 和一个力偶,力偶的力偶矩为 {M}_{\mathrm{f}} ,如图 15b 所示。力 {\mathbf{F}}_{\mathrm{R}} 可分解为静摩擦力 {\mathbf{F}}_{\mathrm{s}} 和正压力 {\mathbf{F}}_{\mathrm{N}} ,力偶矩为 {M}_{\mathrm{f}} 的力偶称为滚动摩擦力偶,它与力偶 \left( {\mathbf{F},{\mathbf{F}}_{\mathrm{s}}}\right) 平衡, 它的转向与滚动的趋向相反,如图 15c 所示。
图14
图 15
与静摩擦力相似,滚动摩擦力偶矩 {M}_{\mathrm{f}} 随着主动力偶矩的增加而增大,当力 F 增加到某个值时, 滚子处于将滚未滚的临界平衡状态,这时, 滚动摩擦力偶矩达到最大值,称之为最大滚动摩擦力偶矩,用 {M}_{\max } 表示。若力 \mathbf{F} 再增大一点,轮子就会滚动。与滑动不同,轮子在滚动过程中,滚动摩擦力偶矩近似等于 {M}_{\max } 。
由此可知,滚动摩擦力偶矩 {M}_{\mathrm{f}} 的大小介于零与最大值之间,即
实验表明:最大滚动摩擦力偶矩 {M}_{\max } 与滚子半径无关,与支承面的正压力(法向约束力) {\mathbf{F}}_{\mathrm{N}} 的大小成正比,即
称此为滚动摩擦定律,其中 \delta 是比例常数,称为滚动摩擦系数。由上式知,滚动摩擦系数具有长度的量纲,单位一般为 \mathrm{{mm}} 。
滚动摩擦系数由实验测定, 它与滚子和支承面的材料的硬度和湿度等有关, 与滚子的半径无关。表 2 是几种材料的滚动摩擦系数。
表 2 几种材料的滚动摩擦系数
| 材料名称 | δ/mm | 材料名称 | δ/mm |
| 铸铁与铸铁 | 0.5 | 软钢与钢 | 0.5 |
| 钢质车轮与钢轨 | 0.05 | 有滚珠轴承的料车与钢轨 | 0.09 |
| 木与钢 | 0.3~0.4 | 无滚珠轴承的料车与钢轨 | 0.21 |
| 木与木 | 0.5~0.8 | 钢质车轮与木面 | 1.5 ~ 2.5 |
| 软木与软木 | 1.5 | 轮胎与路面 | 2~10 |
| 淬火钢珠与钢 | 0.01 |
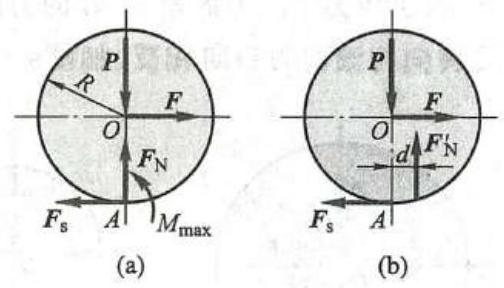
滚动摩擦系数的物理意义如下:滚子在即将滚动的临界平衡状态时,其受力图如图 16a 所示。根据力的平移定理,可将其中的法向约束力 {\mathbf{F}}_{\mathrm{N}} 与最大滚动摩擦力偶 {M}_{\max } 合成为一个力 {\mathbf{F}}_{\mathrm{N}}^{\prime } ,且 {F}_{\mathrm{N}}^{\prime } = {F}_{\mathrm{N}} 。力 {\mathbf{F}}_{\mathrm{N}}^{\prime } 的作用线距中心线的距离为 d ,如图 16b 所示。而
图 16
与式 (7) 比较, 得
因而滚动摩擦系数 \delta 可看成轮在即将滚动时,法向约束力 {\mathbf{F}}_{\mathrm{N}}^{\prime } 离中心线的最远距离,也就是最大滚动摩擦力偶 \left( {{\mathbf{F}}_{\mathrm{N}}^{\prime },\mathbf{P}}\right) 的力偶臂,故它具有长度的量纲。它的意义是, 在主动力的作用下, 接触面间发生的微小变形所引起的等效支持力向前移动的距离。因为这个变形量一般非常小,所以其单位一般为 \mathrm{{mm}} 。
由于滚动摩擦系数较小,因此,在大多数情况下滚动摩擦忽略不计。
由图 16a,可以分别计算出使滚子滚动或滑动所需要的水平拉力 \mathbf{F} ,以分析究竟是使滚子滚动省力还是使滚子滑动省力。
由平衡方程 \sum {M}_{A}\left( \mathbf{F}\right) = 0 ,可以求得
由平衡方程 \sum {F}_{x} = 0 ,可以求得
一般情况下, 有
因而使滚子滚动比滑动省力得多。
例 6 半径为 R 的滑轮 B 上作用有力偶,轮上绕有细绳拉住半径为 R 、重量为 P 的圆柱, 如图 17a 所示。斜面倾角为 \theta ,圆柱与斜面间的滚动摩擦系数为 \delta 。求保持圆柱平衡时,力偶矩 {M}_{B} 的最大与最小值。
解:取圆柱为研究对象, 先求绳子拉力。圆柱在即将滚动的临界状态下, 滚动摩擦力偶矩达最大值,即 {M}_{\max } = \delta {F}_{N} ,转向与滚动趋势相反。当绳拉力为最小值时,圆柱有向下滚动的趋势,当绳拉力为最大值时,圆柱有向上滚动的趋势。
(1) 先求最小拉力 {F}_{\mathrm{T}1} ,受力如图 17b 所示,列平衡方程:
\sum {M}_{A}\left( F\right) = 0,\;P\sin \theta \cdot R - {F}_{\mathrm{{TI}}} \cdot R - {M}_{\max } = 0 \tag{a}\sum {F}_{y} = 0,\;{F}_{\mathrm{N}} - P\cos \theta = 0 \tag{b}图 17
临界状态的补充方程为
{M}_{\max } = \delta {F}_{\mathrm{N}} \tag{c}联立求得最小拉力值为
{F}_{\mathrm{T}1} = P\left( {\sin \theta - \frac{\delta }{R}\cos \theta }\right)(2)再求最大拉力 {\mathbf{F}}_{12} ,受力图如图 17c 所示,列平衡方程:
\sum {M}_{A}\left( F\right) = 0,\;P\sin \theta \cdot R - {F}_{\mathrm{T}2} \cdot R + {M}_{\max } = 0 \tag{d}\sum {F}_{y} = 0,\;{F}_{N} - P\cos \theta = 0 \tag{e}临界状态的补充方程为
{M}_{\max } = \delta {F}_{\mathrm{N}} \tag{f}联立求得最大拉力值为
{F}_{12} = P\left( {\sin \theta + \frac{\delta }{R}\cos \theta }\right)(3)以滑轮 B 为研究对象,受力图如图 17d 所示,列平衡方程:
\sum {M}_{B}\left( F\right) = 0,\;{F}_{\mathrm{T}}^{\prime } \cdot R - {M}_{B} = 0当绳拉力分别为 {\mathbf{F}}_{\mathrm{T}1} 与 {\mathbf{F}}_{\mathrm{T}2} 时,得力偶矩 {M}_{B} 的最大值与最小值为
{M}_{B\max } = {F}_{\mathrm{T}2}R = P\left( {R\sin \theta + \delta \cos \theta }\right){M}_{B\min } = {F}_{\mathrm{{TI}}}R = P\left( {R\sin \theta - \delta \cos \theta }\right)即力偶矩 {M}_{B} 的范围为
P\left( {R\sin \theta - \delta \cos \theta }\right) \leq {M}_{B} \leq P\left( {R\sin \theta + \delta \cos \theta }\right)