平面汇交力系

[Max]

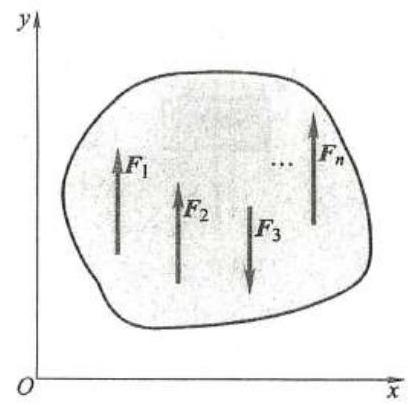
当力系中各力的作用线处于同一平面内时， 该力系称为平面力系。平面力系又可分为平面汇交 (共点) 力系、平面力偶系、平面平行力系、平面任意力系。

1 平面汇交力系

平面汇交力系是指各力的作用线都在同一平面内且汇交于一点的力系。

1.1 平面汇交力系合成的几何法、力多边形法则

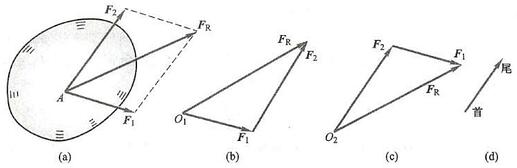
如图 1a 所示，在刚体上点 A 作用两个力 {F}_{1} 和 {F}_{2} ，由力的平行四边形法则， 这两个力可以合成为一个力 {\mathbf{F}}_{\mathrm{R}} 。实际上，此两力的合力也可从任一点 {O}_{1} 或 {O}_{2} 画如图 1b、c 所示的图而求出。这两个由力构成的三角形均称为力三角形。这两个三角形虽然有所不同，但是若把力矢的起端称为首，箭头端称为尾，如图 1d 所示，这两个三角形各分力矢在顶点处均为首尾相接，而合力矢是从初始的力矢首与末了的力矢尾相连。

图 1

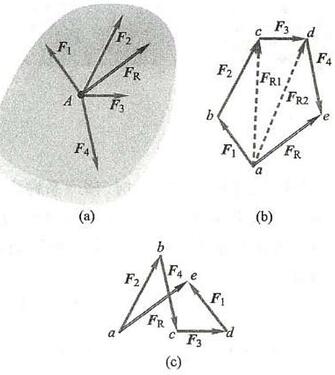
设一刚体受到平面汇交力系 {\mathbf{F}}_{1}\text{、}{\mathbf{F}}_{2}\text{、}{\mathbf{F}}_{3} 和 {\mathbf{F}}_{4} 的作用，各力作用线汇交于点 A ， 根据刚体内部力的可传性，可将各力沿其作用线移至汇交点 A ，如图 2a 所示。

图 2

为合成此力系， 根据上述方法， 逐步两两合成各力， 最后求得一个通过汇交点 A 的合力 {\mathbf{F}}_{\mathrm{R}} 。任取一点 a ，先做力三角形求出 {\mathbf{F}}_{1} 和 {\mathbf{F}}_{2} 的合力 {\mathbf{F}}_{\mathrm{R}1} 的大小与方向， 再做力三角形合成 {F}_{\mathrm{R}1} 与 {\mathbf{F}}_{3} 得 {\mathbf{F}}_{\mathrm{R}2} ，最后合成 {\mathbf{F}}_{\mathrm{R}2} 与 {\mathbf{F}}_{4} 得 {\mathbf{F}}_{\mathrm{R}} ，则 {\mathbf{F}}_{\mathrm{R}} 即为力系的合力，如图 2b 所示。多边形 abcde 称为此平面汇交力系的力多边形，此力多边形的矢序规则是各分力矢依次首尾相接。由此组成的力多边形 {abcde} 有一缺口，故称为不封闭的力多边形，矢量 \overrightarrow{ae} 即表示了此平面汇交力系的合力 {\mathbf{F}}_{\mathrm{R}} 的大小与方向。 当然，合力的作用线仍通过原汇交点 A ，如图 2a 所示的 {\mathbf{F}}_{\mathrm{R}} 。还可注意到，在做力多边形，即求力系的合力时，图 2b 中的虚线不必画出。

根据矢量相加的交换律，任意交换各分力矢的做图次序，可得形状不同的力多边形，但其合力矢不变，如图 2c 所示。

总之， 平面汇交力系可简化为一合力， 其合力的大小与方向等于各分力的矢量和 (几何和)，合力的作用线通过汇交点。设平面汇交力系包含 n 个力，以 {\mathbf{F}}_{\mathrm{R}} 表示它们的合力矢，则有

{\mathbf{F}}_{\mathrm{R}} = {\mathbf{F}}_{1} + {\mathbf{F}}_{2} + \cdots + {\mathbf{F}}_{n} = \mathop{\sum }\limits_{{i = 1}}^{n}{\mathbf{F}}_{i}

为了书写方便， 在无混淆的情况下， 一般均略去求和号中的 i = 1， n ，把上式写为式 (1)

{\mathbf{F}}_{\mathrm{R}} = \sum {\mathbf{F}}_{i} \tag{ 1 }

如力系中各力的作用线都沿同一直线， 则此力系称为共线力系， 它是平面汇交力系的特殊情况， 它的力多边形在同一直线上。若沿直线的某一指向为正， 相反为负， 则力系合力的大小与方向取决于各分力的代数和， 即

{F}_{\mathrm{R}} = \sum {F}_{i} \tag{2}

1.2 平面汇交力系平衡的几何条件

由于平面汇交力系可用其合力来代替， 显然， 平面汇交力系平衡的必要和充分条件是:该力系的合力等于零。用矢量式表示，即

\sum {\mathbf{F}}_{i} = \mathbf{0} \tag{3}

在平衡情形下， 力多边形中最后一力的尾与第一力的首重合， 此时的力多边形称为封闭的力多边形。于是， 可得结论: 平面汇交力系平衡的必要和充分条件是该力系的力多边形自行封闭，这就是平面汇交力系平衡的几何条件。

求解平面汇交力系的平衡问题时可用几何法， 即首先按比例先画出封闭的力多边形， 然后用尺和量角器在图上量得所要求的未知量。对汇交于一点的三个力来说， 现在常常根据图形的几何关系， 画出封闭的力三角形， 用三角公式计算出所要求的未知量。

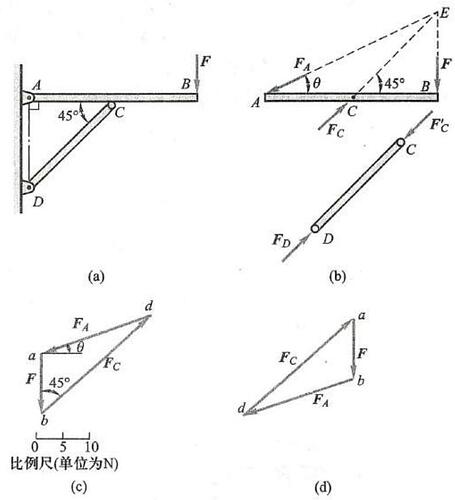
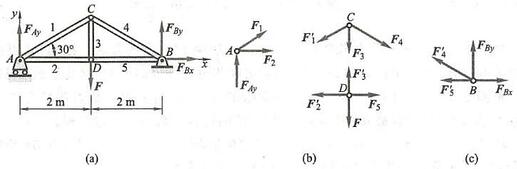
例 1 平面结构如图 3a 所示，杆 {AB} 与杆 {CD} 在点 C 用铰链连接，并在 A\text{、}D 处用铰链连接在铅垂墙上。已知 {AC} = {CB} ，角度如图所示，不计各构件自重，在 B 处作用一铅垂力 F = {10}\mathrm{{kN}} 。 求杆 {CD} 的受力和铰链支座 A 处的约束力。

图 3

解: 选取杆 {AB} 为研究对象。杆 {AB} 在 B 处受载荷 F 作用。杆 {CD} 为二力杆，它对杆 C 处的约束力 {\mathbf{F}}_{c} 的作用线必沿两铰链 D\text{、}C 中心的连线。铰链 A 的约束力 {\mathbf{F}}_{A} 的作用线可根据三力平衡汇交定理确定，即通过另两个力的交点 E ，如图 3b 所示。

根据平面汇交力系平衡的几何条件， 这三个力应组成一封闭的力三角形。先画出已知力 \overrightarrow{ab} = \mathbf{F} ，再由点 a 做直线平行于 {AE} ，由点 b 做直线平行于 {CE} ，这两条直线相交于点 d ，如图 3c 所示。由力三角形 {abd} 封闭，可确定出 {\mathbf{F}}_{c} 和 {\mathbf{F}}_{A} 的指向如图所示。

在图 3c 中，线段 {bd} 和 {da} 分别表示力 {\mathbf{F}}_{c} 和 {\mathbf{F}}_{A} 的大小，量出它们的长度，按比例换算即可得 {\mathbf{F}}_{c} 与 {\mathbf{F}}_{A} 的大小。但一般都是利用三角公式计算，对图 3c 所示力三角形，由正弦定理， 有

\frac{{F}_{c}}{\sin \left( {{90}^{ \circ } + \theta }\right) } = \frac{F}{\sin \left( {{45}^{ \circ } - \theta }\right) }，\;\frac{{F}_{A}}{\sin {45}^{ \circ }} = \frac{F}{\sin \left( {{45}^{ \circ } - \theta }\right) }

式中

\tan \theta = \frac{1}{2}，\;\theta = {26.56}^{ \circ }

解得

{F}_{C} = {28.28}\mathrm{{kN}}，\;{F}_{A} = {22.36}\mathrm{{kN}}

根据作用力和反作用力的关系，可知杆 {CD} 受压力，如图 3b 所示。

也可画出封闭力三角形如图 3d 所示，可得同样结果。

1.3 平面汇交力系合成与平衡的解析法

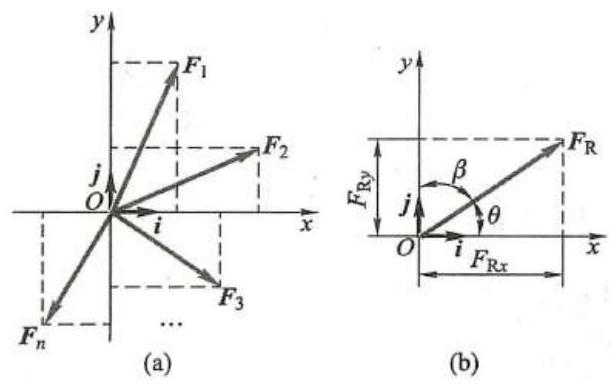
设由 n 个力组成的平面汇交力系作用于一个刚体上，以汇交点 O 作为坐标原点，建立直角坐标系 {Oxy} ，如图 4a 所示。此汇交力系的合力 {\mathbf{F}}_{\mathrm{R}} 的解析表达式为

{\mathbf{F}}_{\mathrm{R}} = {\mathbf{F}}_{\mathrm{R}x} + {\mathbf{F}}_{\mathrm{R}y} = {F}_{\mathrm{R}x}\mathbf{i} + {F}_{\mathrm{R}y}\mathbf{j} \tag{4}

式中， {F}_{\mathrm{R}x}\text{、}{F}_{\mathrm{R}y} 为合力 {F}_{\mathrm{R}} 在 x\text{、}y 轴上的投影，如图 4b 所示。有

{F}_{\mathrm{R}x} = {F}_{\mathrm{R}}\cos \theta ，\;{F}_{\mathrm{R}y} = {F}_{\mathrm{R}}\sin \theta \tag{5}

图 4

根据合矢量投影定理：合矢量在某一轴上的投影等于各分矢量在同一轴上投影的代数和，将式 (1) 向 x 、 y 轴投影，可得

\left. \begin{array}{l} {F}_{\mathrm{R}x} = {F}_{1x} + {F}_{2x} + \cdots + {F}_{nx} = \sum {F}_{x} \\ {F}_{\mathrm{R}y} = {F}_{1y} + {F}_{2y} + \cdots + {F}_{ny} = \sum {F}_{y} \end{array}\right\} \tag{6}

其中， {F}_{1x} 和 {F}_{1y}，{F}_{2x} 和 {F}_{2y}，\cdots ，{F}_{nx} 和 {F}_{ny} 分别为各分力在 x 和 y 轴上的投影。

合力矢的大小和方向余弦为

\left. \begin{array}{l} {F}_{\mathrm{R}} = \sqrt{{F}_{\mathrm{R}x}^{2} + {F}_{\mathrm{R}y}^{2}} = \sqrt{{\left( \sum {F}_{x}\right) }^{2} + {\left( \sum {F}_{y}\right) }^{2}} \\ \cos \left( {{F}_{\mathrm{R}}， i}\right) = \sum {F}_{x}/{F}_{\mathrm{R}}，\;\cos \left( {{F}_{\mathrm{R}}， j}\right) = \sum {F}_{y}/{F}_{\mathrm{R}} \end{array}\right\} \tag{7}

由此， 可求出合力的大小和方向， 当然， 合力的作用点仍在汇交点。这就是平面汇交力系求合力的解析法公式。

由式 (3) 知，平面汇交力系平衡的必要和充分条件是: 该力系的合力 {\mathbf{F}}_{\mathrm{R}} 等于零。由式(4)和式(6)有

\sum {F}_{x} = 0，\;\sum {F}_{y} = 0 \tag{8}

于是， 平面汇交力系平衡的解析条件是该力系中各力在两个坐标轴上投影的代数和分别等于零。式 (8) 称为平面汇交力系的平衡方程， 是两个独立的平衡方程， 可以求解两个未知量。

下面举一例说明平面汇交力系平衡方程的应用。

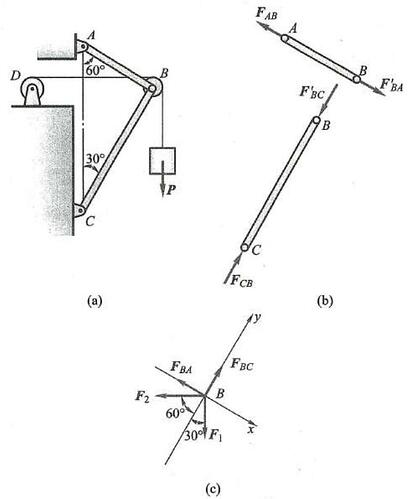
例 2 如图 5a 所示，重物重 P = {20}\mathrm{{kN}} ，用钢丝绳连接如图所示。不计杆、钢丝绳和滑轮 B 的重量，忽略轴承摩擦和滑轮 B 的大小，角度如图所示。求平衡时杆 {AB}\text{、}{BC} 所受的力。

图 5

解:(1)取研究对象。由于杆 {AB} 和杆 {BC} 都是二力杆，假设杆 {AB} 受拉力、杆 {BC} 受压力，如图 5b 所示。为了求出这两个未知力，可通过求两杆对滑轮 B 的约束力解决。因此，选取滑轮 B 为研究对象。

(2)画受力图。滑轮 B 受到钢丝绳的拉力 {F}_{1} 和 {F}_{2}\left( {{F}_{1} = {F}_{2} = P}\right) 作用。杆 {AB} 和杆 {BC} 对滑轮 B 的约束力以 {\mathbf{F}}_{BA} 和 {\mathbf{F}}_{BC} 表示。由于滑轮的大小忽略不计，这些力可看作是汇交力系，如图 5c所示。

(3)列平衡方程。为避免解联立方程， 选取坐标轴如图所示。列出的平衡方程为

\sum {F}_{x} = 0，\; - {F}_{BA} + {F}_{1}\cos {60}^{ \circ } - {F}_{2}\cos {30}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{BC} - {F}_{1}\cos {30}^{ \circ } - {F}_{2}\cos {60}^{ \circ } = 0

(4)求解方程。代入数据，分别解得

{F}_{BA} = - {7.32}\mathrm{{kN}}\;{F}_{BC} = {27.32}\mathrm{{kN}}

分析所求结果， {\mathbf{F}}_{BC} 为正值，表示力的方向与假设方向相同，即杆 {BC} 受压; {\mathbf{F}}_{BA} 为负值，表示力的方向与假设方向相反，即杆 {AB} 也受压。

2 平面力对点之矩 · 平面力偶

力对刚体的作用效应使刚体的运动状态发生改变，包括移动与转动，力对刚体的移动效应可用力矢来度量， 而力对刚体的转动效应可用力对点的矩 (简称力矩) 来度量， 即力矩是度量力对刚体转动效应的物理量。

2.1 力对点之矩 (力矩)

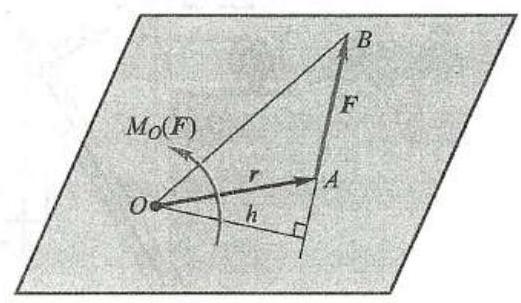
图 6

如图 6 所示，力 \mathbf{F} 与点 O 位于同一平面内，点 O 称为矩心，点 O 到力 \mathbf{F} 作用线的垂直距离 h 为力臂，在此平面中，力 \mathbf{F} 使物体绕点 O 转动的效果，取决于两个要素:

(1)力的大小 F 与力臂 h (矩心到力作用线的距离)的乘积;

(2)力使物体绕矩心转动的方向。

在平面问题中力对点的矩的定义如下:

力对点之矩是一个代数量，其绝对值等于力的大小与力臂的乘积，其转向用正负号确定，其规定为:力使物体绕矩心逆时针转向转动时为正，反之为负。

力 \mathbf{F} 对点 O 的矩以 {M}_{0}\left( \mathbf{F}\right) 表示，即

{M}_{o}\left( \mathbf{F}\right) = \pm {Fh} \tag{9}

显然， 当力的作用线通过矩心， 即力臂等于零时， 它对矩心的力矩等于零。

力矩的常用单位为 \mathrm{N} \cdot \mathrm{m} 或 \mathrm{{kN}} \cdot \mathrm{m} 。

为和后面空间力对点的矩对应，以 r 表示由点 O 到点 A 的矢径 (图 6)，平面力 \mathbf{F} 对点 O 的矩，由矢积定义，可以表示为 \mathbf{r} \times \mathbf{F} ，此矢积的模就是力矩的大小 {Fh} ， 此矢积的方向，即力矩的转向符合矢量叉乘的右手法则。

2.2 合力矩定理与力矩的解析表达式

合力矩定理:平面汇交力系的合力对于平面内任一点之矩等于所有各分力对于该点之矩的代数和， 以公式表示为

{M}_{0}\left( {\mathbf{F}}_{\mathrm{R}}\right) = \sum {M}_{0}\left( {\mathbf{F}}_{i}\right) \tag{10}

式中， {\mathbf{F}}_{\mathrm{R}} 为平面汇交力系的合力， {\mathbf{F}}_{t} 为各分力。 按力系等效概念，上式必然成立，且式 (10) 适用于任何有合力存在的力系。

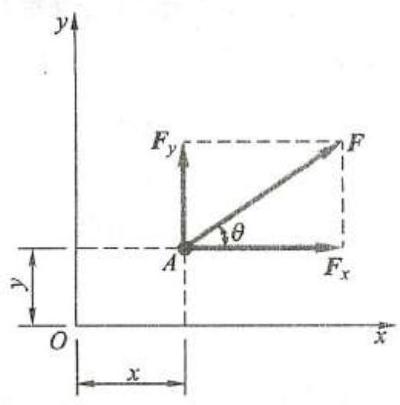
图 7

由合力矩定理， 在直角坐标系中， 如图 7 所示，已知力 F ，作用点的坐标 A\left( {x， y}\right) 与夹角 \theta 。力 \mathbf{F} 对坐标原点 O 之矩，可按式(10)，通过其分力 {\mathbf{F}}_{x} 与 {\mathbf{F}}_{y} 对点 O 之矩而得到，即

{M}_{0}\left( \mathbf{F}\right) = {M}_{0}\left( {\mathbf{F}}_{x}\right) + {M}_{0}\left( {\mathbf{F}}_{y}\right)

= F\sin \theta \cdot x - F\cos \theta \cdot y

或

{M}_{0}\left( \mathbf{F}\right) = x{F}_{y} - y{F}_{x} \tag{11}

此式称为平面内力对点之矩的解析表达式。式中， x\text{、}y 为力 \mathbf{F} 作用点的坐标， {F}_{x} 、 {F}_{y} 为力 F 在 x 、 y 轴的投影。计算时用它们的代数量代入。

将式 (11) 代入式 (10)，可得合力 {\mathbf{F}}_{\mathrm{R}} 对坐标原点之矩的解析表达式，即

{M}_{O}\left( {\mathbf{F}}_{\mathrm{R}}\right) = \sum {M}_{O}\left( {\mathbf{F}}_{i}\right) = \sum \left( {{x}_{i}{F}_{iy} - {y}_{i}{F}_{ix}}\right) \tag{12}

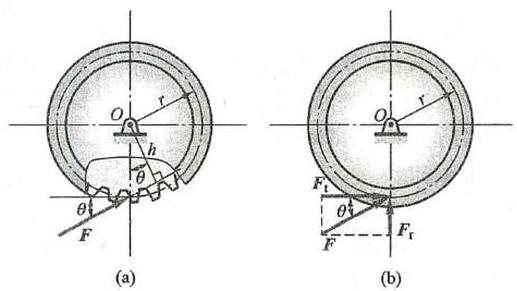
例 3 如图 8a 所示，圆柱直齿轮受到另一齿轮对其啮合力 \mathbf{F} 的作用，大小为 F = {1400}\mathrm{\;N} ，压力角 \theta = {20}^{ \circ } ，齿轮的节圆 (啮合圆) 半径 r = {60}\mathrm{\;{mm}} ，求力 F 对于轴心 O 的力矩。

图 8

解: 计算力 F 对点 O 的矩，可直接按力矩的定义求得 (图 8a)，即

{M}_{0}\left( F\right) = F \cdot h = F \cdot r\cos \theta = {78.93}\mathrm{\;N} \cdot \mathrm{m}

也可以根据合力矩定理，将力 F 分解为圆周力 {F}_{\mathrm{t}} 和径向力 {F}_{\mathrm{r}} (图 8b)，由于径向力 {F}_{\mathrm{r}} 通过矩心 O ，则

{M}_{0}\left( F\right) = {M}_{0}\left( {F}_{\mathrm{t}}\right) + {M}_{0}\left( {F}_{\mathrm{r}}\right) = {M}_{0}\left( {F}_{\mathrm{t}}\right) = F\cos \theta \cdot r = {78.93}\mathrm{\;N} \cdot \mathrm{m}

两种方法的计算结果相同。

图 9

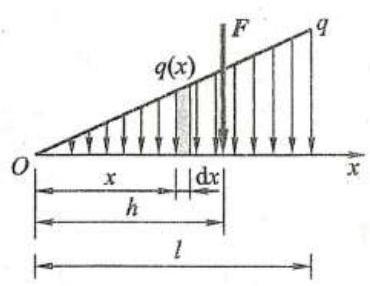
在实际问题中有时遇到图 9 所示的三角形分布载荷，一般已知其分布长度为 l (单位为 \mathrm{m} )，单位长度分布载荷的最大值为 q( 单位为 \mathrm{N}/\mathrm{m} 或 \mathrm{{kN}}/\mathrm{m} )。实际计算时，为方便计算，往往要用其合力来代替此分布力。 为求其合力大小和作用线位置， 可以用积分的方法求出其合力大小， 用合力矩定理可求出其合力作用线位置。现推导如下：

设距 O 端为 x 的微段处的载荷为 q\left( x\right) ，由相似三角形的关系，有 \frac{q\left( x\right) }{x} = \frac{q}{l} ，则 q\left( x\right) = \frac{q}{l}x ，微段 \mathrm{d}x 上的合力为 q\left( x\right) \cdot \mathrm{d}x ，因此，三角形分布载荷的合力大小 F 为

F = {\int }_{0}^{l}\frac{q}{l}x \cdot \mathrm{d}x = \frac{1}{2}{ql}

设合力作用线距 O 端的距离为 h ，微段 \mathrm{d}x 上的微小力对点 O 的力矩为 q\left( x\right) \cdot \mathrm{d}x \cdot x ， 由合力矩定理， 有

F \cdot h = {\int }_{0}^{l}\frac{q}{l}{x}^{2} \cdot \mathrm{d}x = \frac{1}{3}q{l}^{2}

解得

h = \frac{2}{3}l

所以，三角形分布载荷的合力大小为 \frac{1}{2}{ql} ，合力作用线距点 O 的距离为 \frac{2}{3}l ，当然，合力的方向和分布力的方向相同。以后在实际计算时， 此结论可作为公式使用。

图 10

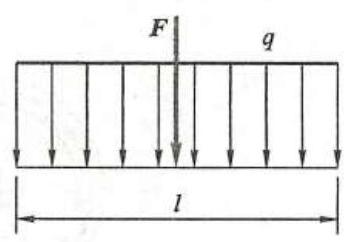
在实际问题中还会遇到图 10 所示的均布载荷，显然其合力大小为 {ql} ，合力作用线位置在均布载荷的正中间， 方向和各分力方向相同，此结论也可以直接使用。

2.3 力偶与力偶矩

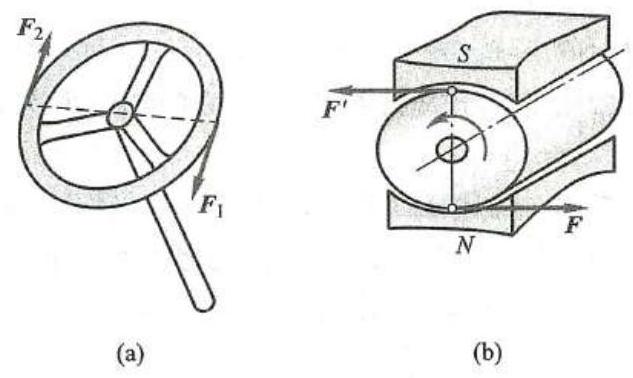
在日常生活与工程实际中，常常见到汽车司机用双手转动方向盘 (图 11a)、 电动机的定子磁场对转子作用电磁力使之旋转 (图 11b) 、钳工用丝锥攻螺纹等。 在方向盘、电动机转子、丝锥等物体上，都作用了成对的等值、反向且不共线的平行力。等值、反向平行力的矢量和等于零，但是由于它们不共线而不能相互平衡，它们能使物体改变转动状态。这种由两个大小相等、方向相反且不共线的平行力组成的力系，称为力偶，如图 12 所示，记作 \left( {\mathbf{F}，{\mathbf{F}}^{\prime }}\right) 。力偶的两力之间的垂直距离 d 称为力偶臂， 力偶所在的平面为力偶的作用面。

因为力偶中的两个力等值、反向、平行且不共线，所以力偶不能合成为一个力， 或用一个力等效替换， 因此， 力偶也不能用一个力来平衡。力和力偶是静力学的两个基本要素。

力偶是由两个力组成的特殊力系，它的作用只改变物体的转动状态。与平面力对点的矩类似， 在力偶作用面内， 力偶使物体转动的效果， 也取决于两个要素：

图 11

图 12

(1)力偶中力的大小 F 与力偶臂 d 的乘积；

(2)力偶在作用面内转动的方向。

为此， 在平面中， 有力偶矩的定义：在力偶作用面内， 力偶矩是一个代数量， 其绝对值等于力的大小与力偶臂的乘积， 其转向用正负号确定， 其规定为: 力偶使物体逆时针转向为正， 反之为负。以公式表示为

M = \pm F \cdot d = \pm 2{A}_{\bigtriangleup {ABC}} \tag{13}

力偶矩的单位和力矩的单位相同。力偶矩也可以用 \bigtriangleup {ABC} 的面积 {A}_{\bigtriangleup {ABC}} 表示， 如图 12 所示。

2.4 力偶的性质

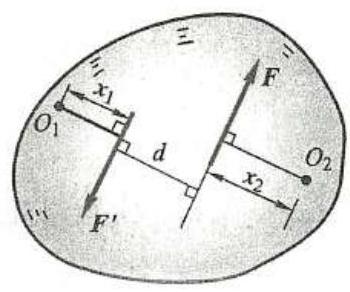
(1)力偶对任意点取力矩都等于力偶矩， 不因矩心的改变而改变。

图 13

如图 13 所示，该力偶的力偶矩为 {Fd} ，在力偶所在平面内任取一点 {O}_{1} ，将力偶中的两个力对此点取力矩， 有

{M}_{{O}_{1}}\left( F\right) + {M}_{{O}_{1}}\left( {F}^{\prime }\right) = F \cdot \left( {d + {x}_{1}}\right) - {F}^{\prime } \cdot {x}_{1} = {Fd}

对点 {O}_{2} 取力矩，有

{M}_{{O}_{2}}\left( F\right) + {M}_{{O}_{2}}\left( {F}^{\prime }\right) = - F \cdot {x}_{2} + {F}^{\prime } \cdot \left( {{x}_{2} + d}\right) = {Fd}

可见力偶对任何点取力矩都等于力偶矩， 不因矩心的改变而改变。这就证明了力偶的这一性质。

力矩和力偶矩都是力对物体转动效果的度量， 但二者显然有所不同。力偶对任何点取力矩都等于力偶矩， 不因矩心的改变而改变; 而力矩就不同， 一般矩心若改变，其力矩就改变。这是力矩与力偶矩的一个重要区别。

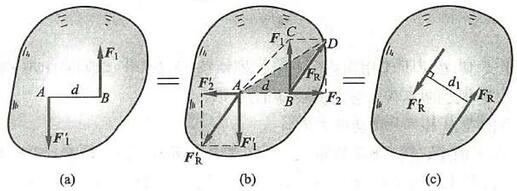
(2)只要保持力偶矩不变，力偶可在其作用面内任意移转，且可以同时改变力偶中力的大小与力偶臂的长短，对刚体的作用效果不变。

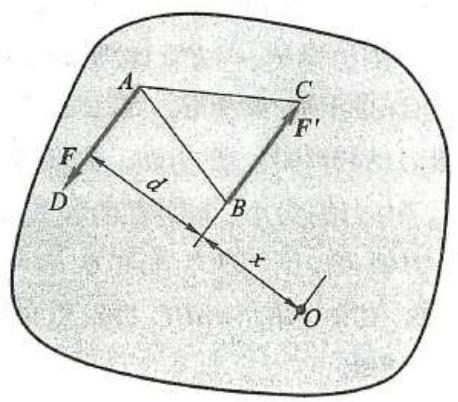
如图 14a 所示，刚体上有一力偶 \left( {{F}_{1}，{F}_{1}^{\prime }}\right) 作用，其力偶矩为 {F}_{1}d ，据加减平衡力系原理，在 A\text{、}B 两点加一平衡力系 {\mathbf{F}}_{2} = - {\mathbf{F}}_{2}^{\prime } ，如图 14b 所示，再据力的平行四边形法则，把 A\text{、}B 两点的力合成分别得力 {\mathbf{F}}_{\mathrm{R}}\text{、}{\mathbf{F}}_{\mathrm{R}}^{\prime } ，显然此两力构成一力偶 \left( {\mathbf{F}}_{\mathrm{R}}\right. ， \left. {F}_{\mathrm{R}}^{\prime }\right) ，其力偶矩为 {F}_{\mathrm{R}}{d}_{1} ，再据力的可传性，把力 {F}_{\mathrm{R}}\text{、}{F}_{\mathrm{R}}^{\prime } 传递，如图 14c 所示，很明显，力偶 \left( {{\mathbf{F}}_{1}，{\mathbf{F}}_{1}^{\prime }}\right) 和 \left( {{\mathbf{F}}_{\mathrm{R}}，{\mathbf{F}}_{\mathrm{R}}^{\prime }}\right) 中力的大小、力偶臂的长短、力的作用点、力的方向均已改变，但两力偶等效。而力偶 \left( {{\mathbf{F}}_{1}，{\mathbf{F}}_{1}^{\prime }}\right) 的力偶矩为 {Fd} = 2{A}_{\bigtriangleup {ABC}} ，力偶 \left( {{\mathbf{F}}_{\mathrm{R}}，{\mathbf{F}}_{\mathrm{R}}^{\prime }}\right) 的力偶矩为 {F}_{\mathrm{R}}{d}_{1} = 2{A}_{\bigtriangleup {ABD}} ，显然，直角三角形 {ABC} 与斜三角形 {ABD} 的面积相等，所以两力偶的力偶矩相等， 此性质得证。

图 14

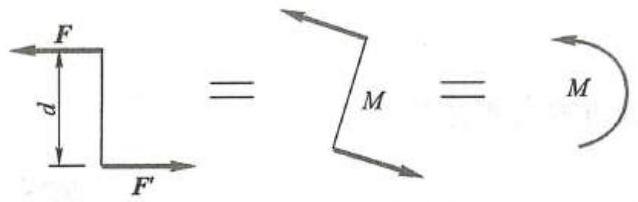
由于力偶具有这样的性质， 同时也为画图方便计， 以后常用图 15 所示符号表示力偶与力偶矩。

图 15

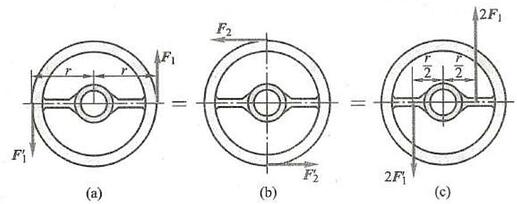
图 16 所示为驾驶员给方向盘的三种施力方式，图中 {F}_{1} = {F}_{1}^{\prime } = {F}_{2} = {F}_{2}^{\prime } ，即是说明此性质的一个实例。

图 16

2.5 平面力偶系的合成和平衡条件

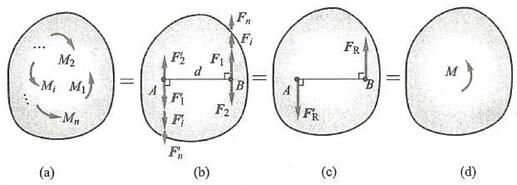
设在同一平面内有 n 个力偶作用，形成一平面力偶系，如图 17a 所示，其力偶矩分别为 {M}_{1}，{M}_{2}，\cdots ，{M}_{i}，\cdots ，{M}_{n} ，其中， {M}_{2} 为顺时针方向 (为负)，在此平面内任选一段距离 {AB} = d ，令

\frac{{M}_{1}}{d} = {F}_{1}，\frac{{M}_{2}}{d} = {F}_{2}，\cdots ，\frac{{M}_{i}}{d} = {F}_{i}，\cdots ，\frac{{M}_{n}}{d} = {F}_{n}

图 17

即

{M}_{1} = {F}_{1}d，{M}_{2} = {F}_{2}d，\cdots ，{M}_{i} = {F}_{i}d，\cdots ，{M}_{n} = {F}_{n}d

则图 17a 所示平面力偶系与图 17b 所示力系等效，把作用在点 B 的共线力系的合力以 {\mathbf{F}}_{\mathrm{R}} 表示 (图 17c)，有

{F}_{\mathrm{R}} = {F}_{1} - {F}_{2} + \cdots + {F}_{i} + \cdots + {F}_{n}

把作用在点 A 的共线力系的合力以 {F}_{\mathrm{R}}^{\prime } 表示，显然有 {F}_{\mathrm{R}} = - {F}_{\mathrm{R}}^{\prime } ，即此两力形成一力偶，以 M 表示 (图 17d)， M = {F}_{\mathrm{R}}d 。把上式两边同乘以 d ，有

{F}_{\mathrm{R}}d = {F}_{1}d - {F}_{2}d + \cdots + {F}_{i}d + \cdots + {F}_{n}d

即

M = {M}_{1} + {M}_{2} + \cdots + {M}_{i} + \cdots + {M}_{n}

有

M = \sum {M}_{i} \tag{14}

即在同一平面内的任意个力偶，可用一个力偶 M 与之等效，称之为合力偶。因此， 在同一平面内的任意个力偶可合成为一个合力偶， 合力偶矩等于各个力偶矩的代数和。

由合成结果知，平面力偶系平衡时，其合力偶矩应等于零。因此，平面力偶系平衡的必要和充分条件是:所有各力偶矩的代数和等于零。以公式表示为

\sum {M}_{i} = 0 \tag{15}

此即为平面力偶系的平衡条件。

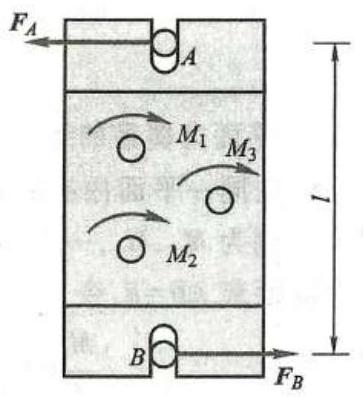
例 4 如图 18 所示的工件， 用多轴钻床在工件上同时钻三个孔， 钻头对工件作用有三个力偶， 其力偶矩分别为 {M}_{1} = {M}_{2} = {10}\mathrm{\;N} \cdot \mathrm{m}，{M}_{3} = {20}\mathrm{\;N} \cdot \mathrm{m} ，固定螺栓 A 和 B 的距离 l = {200}\mathrm{\;{mm}} 。求两个光滑螺栓所受的水平力。

图 18

解: 选工件为研究对象。工件在水平面内受三个力偶和两个螺栓的水平约束力作用。根据力偶系的合成定理，三个力偶合成后仍为一力偶， 如果工件平衡， 必有一力偶与它平衡。 因此，螺栓 A 和 B 的水平约束力 {\mathbf{F}}_{A} 和 {\mathbf{F}}_{B} 必组成一力偶，即有 {F}_{A} = {F}_{B} ，它们的方向假设如图所示。

由力偶系的平衡条件得

\sum {M}_{i} = 0，\;{F}_{A} \cdot l - {M}_{1} - {M}_{2} - {M}_{3} = 0

解得

{F}_{A} = {F}_{B} = \frac{{M}_{1} + {M}_{2} + {M}_{3}}{l}

代入题给数值得

{F}_{A} = {F}_{B} = {200}\mathrm{\;N}

因 {F}_{A}\text{、}{F}_{B} 是正值，故所设方向正确，螺栓所受的力与 {F}_{A}\text{、}{F}_{B} 大小相等，方向相反。

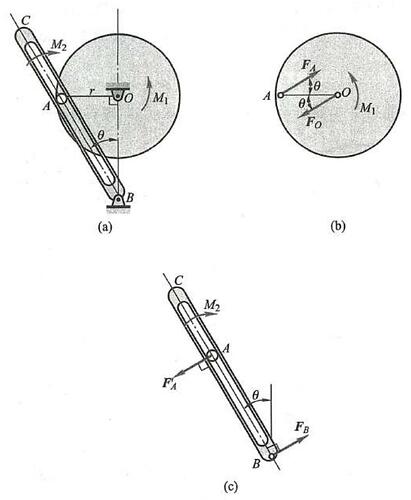
例 5 不计图 19a 所示机构自重，圆轮上的销 A 放在摇杆 {BC} 上的光滑导槽内。圆轮上作用一力偶矩为 {M}_{1} = 2\mathrm{{kN}} \cdot \mathrm{m} 的力偶， {OA} = r = {0.5}\mathrm{\;m} ，图示位置时 {OA} 与 {OB} 垂直， \theta = {30}^{ \circ } ，系统平衡。求作用于摇杆 {BC} 上的力偶矩 {M}_{2} ，铰链 O 、 B 处的约束力。

解: 先取圆轮为研究对象，其上受有力偶矩为 {M}_{1} 的力偶，以及光滑导槽对销 A 的作用力 {\mathbf{F}}_{A} 和铰链 O 处约束力 {\mathbf{F}}_{0} 的作用。由于力偶必须由力偶来平衡，因而 {\mathbf{F}}_{A} 与 {\mathbf{F}}_{0} 必形成一力偶，力偶矩方向与 {M}_{1} 相反，由此定出 {\mathbf{F}}_{A} 与 {\mathbf{F}}_{O} 的方向如图 19b所示。由力偶平衡条件得

\sum {M}_{i} = 0，\;{M}_{1} - {F}_{A} \cdot r\sin \theta = 0

解得

{F}_{A} = \frac{{M}_{1}}{r\sin {30}^{ \circ }} \tag{a}

再以摇杆 {BC} 为研究对象，其上作用有力偶矩为 {M}_{2} 的力偶与力 {\mathbf{F}}_{A}^{\prime }\text{、}{\mathbf{F}}_{B} ，如图 19c 所示。 同理， {\mathbf{F}}_{A}^{\prime } 与 {\mathbf{F}}_{B} 必组成一力偶，由平衡条件得

\sum {M}_{i} = 0，\;{F}_{A}^{\prime } \cdot \frac{r}{\sin \theta } - {M}_{2} = 0 \tag{b}

其中 {F}_{A}^{\prime } = {F}_{A} 。将式 (a) 代入式 (b)，得

{M}_{2} = 4{M}_{1} = 8\mathrm{{kN}} \cdot \mathrm{m}

图 19

{\mathbf{F}}_{O} 与 {\mathbf{F}}_{A} 组成力偶， {\mathbf{F}}_{B} 与 {\mathbf{F}}_{A}^{\prime } 组成力偶，则有

{F}_{O} = {F}_{B} = {F}_{A} = \frac{{M}_{1}}{r\sin {30}^{ \circ }} = 8\mathrm{{kN}}

方向如图 19b、19c 所示。

3 平面任意力系的简化

力系中所有力的作用线都处于同一平面内且任意分布时，称为平面任意力系。 平面任意力系， 不论其怎么复杂， 总可以用一个简单力系等效代替， 称之为平面任意力系的简化。为完成平面任意力系的简化， 要用到力的平移定理。

3.1 力的平移定理

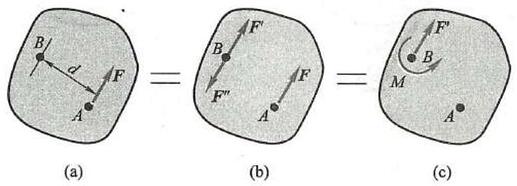
可以把作用在刚体上点 A 的力 \mathbf{F} 平行移到其上任一点 B ，但必须同时附加一个力偶，这个附加力偶的力偶矩等于原来的力 \mathbf{F} 对新作用点 B 的力矩，此为力的平移定理。

证明: 图 20a 中的力 F 作用于刚体的点 A ，在刚体上任取一点 B ，并在点 B 加上一对平衡力 {\mathbf{F}}^{\prime } 和 {\mathbf{F}}^{\prime \prime } ，它们与力 \mathbf{F} 平行，且 F = {F}^{\prime } = {F}^{\prime \prime } ，如图 20b 所示。由加

减平衡力系原理，显然，这 3 个力与原来的一个力 F 等效。这 3 个力又可看作一个作用在点 B 的力 {\mathbf{F}}^{\prime } 和一个力偶 \left( {\mathbf{F}，{\mathbf{F}}^{\prime \prime }}\right) ，此力偶称为附加力偶，显然，附加力偶的力偶矩为

M = {Fd} = {M}_{B}\left( F\right)

为方便计，一般把图 20b 所示，用图 20c 表示，定理得证。

图 20

下面用力的平移定理讨论平面任意力系向任意一点的简化。

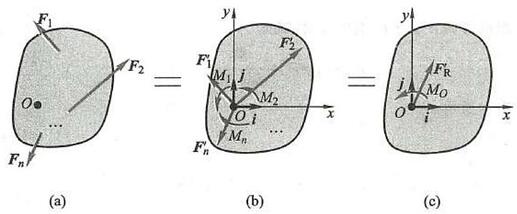
3.2 平面任意力系向作用面内任意一点的简化 · 主矢和主矩

设刚体上有 n 个力 {\mathbf{F}}_{1}，{\mathbf{F}}_{2}，\cdots ，{\mathbf{F}}_{n} 作用，形成一平面任意力系，如图 21a 所示。在此平面内任取一点 O ，称之为简化中心，应用力的平移定理，把各力都平移到点 O 。这样，得到作用于点 O 的力 {\mathbf{F}}_{1}^{\prime }，{\mathbf{F}}_{2}^{\prime }，\cdots ，{\mathbf{F}}_{n}^{\prime } ，以及相应的附加力偶，其力偶矩分别为 {M}_{1}，{M}_{2}，\cdots ，{M}_{n} ，如图 21b 所示。这些附加力偶的力偶矩分别为

{M}_{i} = {M}_{o}\left( {\mathbf{F}}_{i}\right) \;\left( {i = 1，2，\cdots ， n}\right)

图 21

这样， 平面任意力系就由一个平面共点力系和一个平面力偶系等效代替， 把未知问题转化成了已知问题。然后， 再分别合成这两个力系。

作用于点 O 的平面共点力系可合成为一个力 {\mathbf{F}}_{\mathrm{R}}^{\prime } ，如图 21c 所示，因为 {\mathbf{F}}_{i}^{\prime } = {\mathbf{F}}_{i} ，所以有

{\mathbf{F}}_{\mathrm{R}}^{\prime } = \sum {\mathbf{F}}_{i}^{\prime } = \sum {\mathbf{F}}_{i} \tag{16}

即力矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 等于原来各力的矢量和。

平面力偶系可合成为一个力偶，如图 21c 所示，此力偶的力偶矩 {M}_{O} 等于各附加力偶矩的代数和，又等于原来各力对点 O 的力矩的代数和，即

{M}_{o} = \sum {M}_{i} = \sum {M}_{o}\left( {\mathbf{F}}_{i}\right) \tag{17}

平面任意力系中所有各力的矢量和 {\mathbf{F}}_{\mathrm{R}}^{\prime } ，称之为该力系的主矢; 而这些力对于任选中心 O 的力矩的代数和为 {M}_{O} ，称之为该力系对于简化中心的主矩。显然，主矢与简化中心无关， 而主矩一般与简化中心有关， 故必须指明力系是对于哪一点的主矩。

求主矢的大小和方向，类似于平面汇交力系，为方便起见，采用解析法，即主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 的大小和方向余弦一般用下面的公式来计算:

{F}_{\mathrm{R}}^{\prime } = \sqrt{{\left( \sum {F}_{ix}\right) }^{2} + {\left( \sum {F}_{iy}\right) }^{2}}，\;\cos \left( {{F}_{\mathrm{R}}^{\prime }， i}\right) = \frac{\sum {F}_{ix}}{{F}_{\mathrm{R}}^{\prime }}，\;\cos \left( {{F}_{\mathrm{R}}^{\prime }， j}\right) = \frac{\sum {F}_{iy}}{{F}_{\mathrm{R}}^{\prime }} \tag{18}

式中， \sum {F}_{ix}\text{、}\sum {F}_{iy} 分别表示各分力在 x\text{、}y 轴上投影的代数和。

于是可得结论: 在一般情况下，平面任意力系向作用面内任选一点 O 简化，可得一个力和一个力偶， 这个力的大小和方向等于该力系的主矢， 作用线通过简化中心 O 。这个力偶的力偶矩等于该力系对于点 O 的主矩。

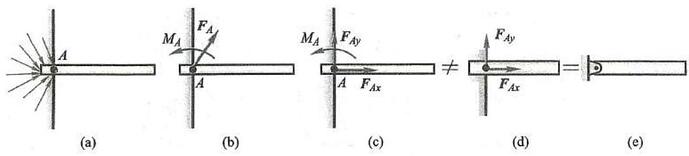
利用平面任意力系的简化结果， 此处再介绍一种类型的约束。当物体的一端完全固结(嵌)于另一物体上，这种约束称为固定端约束。阳台、烟囱、水塔根部的约束及其他许多约束基本上属于固定端约束。对这些约束， 当所有主动力都分布在同一平面内时， 约束力也必定分布在此平面内， 称之为平面固定端约束， 如图 22a所示， 其约束力的分布情况非常复杂， 要搞清楚其分布规律非常困难且没有必要。但由力系简化理论， 该力系可由一个力 (主矢) 与一个力偶 (主矩) 与之等效，如图 22b 所示。一般情况下，该力用它的两个正交分力来表示，如图 22c 所示。

图 22

因此， 平面固定端约束的约束力为两个力与一个力偶。其力学 (物理) 意义可解释为， 此种约束限制物体根部沿两个方向的线位移与绕根部的角位移 (转动)。注意固定端约束有一约束力偶， 如果对固定端约束不画此约束力偶， 只画正交两个力 (图 22d)，则固定端约束与铰链约束无区别 (图 22e)，这样就改变了其约束性质。

3.3 平面任意力系的简化结果分析 - 合力矩定理

平面任意力系向作用面内任一点简化的结果，可能有四种情况，即:
(1) {\mathbf{F}}_{\mathrm{R}}^{\prime } = \mathbf{0} ， {M}_{0} \neq 0 ；
(2) {F}_{\mathrm{R}}^{\prime } \neq 0，{M}_{0} = 0 ；
(3) {F}_{\mathrm{R}}^{\prime } \neq 0，{M}_{0} \neq 0 ；
(4) {F}_{\mathrm{R}}^{\prime } = 0，{M}_{0} = 0 。

下面对这几种情况作进一步的分析讨论。

(1)平面任意力系简化为一个力偶的情形

如果力系的主矢等于零，而主矩 {M}_{o} 不等于零，即

{\mathbf{F}}_{\mathrm{R}}^{\prime } = \mathbf{0}，\;{M}_{0} \neq 0

则原力系合成为合力偶， 合力偶矩为

{M}_{o} = \sum {M}_{o}\left( {\mathbf{F}}_{i}\right)

因为力偶对于平面内任意一点的力偶矩都相同， 所以当力系合成为一个力偶时， 主矩与简化中心的选择无关。

(2)平面任意力系简化为一个合力的情形 · 合力矩定理

如果主矩等于零， 主矢不等于零， 即

{\mathbf{F}}_{\mathrm{R}}^{\prime } \neq \mathbf{0}，\;{M}_{o} = 0

此时附加力偶系互相平衡，只有一个与原力系等效的力 {\mathbf{F}}_{\mathrm{R}}^{\prime } 。显然，力 {\mathbf{F}}_{\mathrm{R}}^{\prime } 就是原力系的合力，而合力的作用线恰好通过选定的简化中心 O 。

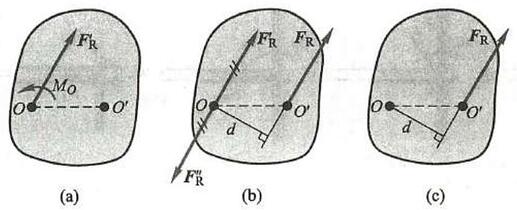
如果平面力系向点 O 简化的结果是主矢和主矩都不等于零，如图 23a 所示， 即

{\mathbf{F}}_{\mathrm{R}}^{\prime } \neq \mathbf{0}，\;{M}_{o} \neq 0

现将力偶矩为 {M}_{0} 的力偶用两个力 {\mathbf{F}}_{\mathrm{R}} 和 {\mathbf{F}}_{\mathrm{R}}^{\prime \prime } 表示，并令 {\mathbf{F}}_{\mathrm{R}}^{\prime } = {\mathbf{F}}_{\mathrm{R}} = - {\mathbf{F}}_{\mathrm{R}}^{\prime \prime } (图 23b)， 再去掉一对平衡力 {\mathbf{F}}_{\mathrm{R}}^{\prime } 与 {\mathbf{F}}_{\mathrm{R}}^{\prime \prime } ，于是就将作用于点 O 的力 {\mathbf{F}}_{\mathrm{R}}^{\prime } 和力偶 \left( {{\mathbf{F}}_{\mathrm{R}}，{\mathbf{F}}_{\mathrm{R}}^{\prime \prime }}\right) 合成为一个作用在点 {O}^{\prime } 的力 {\mathbf{F}}_{\mathrm{R}} ，如图 23 \mathrm{c} 所示。

图 23

这个力 {\mathbf{F}}_{\mathrm{R}} 就是原力系的合力。合力矢的大小和方向等于主矢; 合力的作用线在点 O 的哪一侧，需根据主矢和主矩的方向确定; 合力作用线到点 O 的距离 d 为

d = \frac{{M}_{o}}{{F}_{\mathrm{R}}}

下面证明，平面任意力系的合力矩定理。由图 23c 易见，合力 {\mathbf{F}}_{\mathrm{R}} 对点 O 的

力矩为

{M}_{0}\left( {\mathbf{F}}_{\mathrm{R}}\right) = {F}_{\mathrm{R}}d = {M}_{0}

由式 (17) 有

{M}_{0} = \sum {M}_{0}\left( {\mathbf{F}}_{i}\right)

所以得证

{M}_{0}\left( {\mathbf{F}}_{\mathrm{R}}\right) = \sum {M}_{0}\left( {\mathbf{F}}_{i}\right) \tag{19}

由于简化中心 O 是任意选取的，故上式有普遍意义，可叙述为: 平面任意力系的合力对作用面内任一点的力矩等于力系中各力对同一点的力矩的代数和。这就是合力矩定理。实际上合力矩定理不必证明， 这是由于合力与力系等效， 因此， 合力对任一点的力矩必等于力系中各力对同一点的力矩的代数和。

(3)平面任意力系平衡的情形

如果力系的主矢和主矩均等于零，即

{F}_{\mathrm{R}}^{\prime } = 0，\;{M}_{o} = 0

则原力系平衡， 显然， 此时的简化结果与简化中心的选择无关， 这种情形将在下节详细讨论。

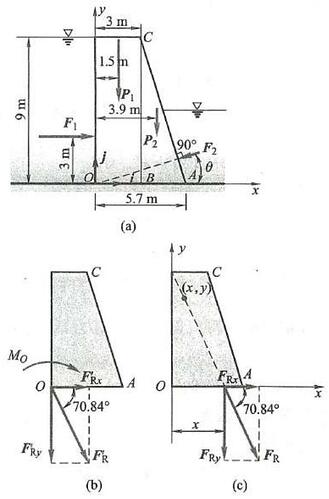
例 6 重力坝受力简图如图 24a 所示，已知 {P}_{1} = {450}\mathrm{{kN}}，{P}_{2} = {200}\mathrm{{kN}}，{F}_{1} = {300}\mathrm{{kN}} ， {F}_{2} = {70}\mathrm{{kN}} 。求力系向点 O 简化的结果，合力与基线 {OA} 的交点到点 O 的距离 x ，以及合力作用线方程。

图 24

解:(1)先将力系向点 O 简化，求得其主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 和主矩 {M}_{0} ，如图 24b 所示。由图 24a，有

\theta = \angle {ACB} = \arctan \frac{AB}{CB} = {16.7}^{ \circ }

主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 在 x 、 y 轴上的投影为

{F}_{\mathrm{R}x}^{\prime } = \sum {F}_{x} = {F}_{1} - {F}_{2}\cos \theta = {232.9}\mathrm{{kN}}

{F}_{\mathrm{R}y}^{\prime } = \sum {F}_{y} = - {P}_{1} - {P}_{2} - {F}_{2}\sin \theta = - {670.1}\mathrm{{kN}}

主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 的大小为

{F}_{\mathrm{R}}^{\prime } = \sqrt{{\left( \sum {F}_{x}\right) }^{2} + {\left( \sum {F}_{y}\right) }^{2}} = {709.4}\mathrm{{kN}}

主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 的方向余弦为

\cos \left( {{F}_{\mathrm{R}}^{\prime }， i}\right) = \frac{\sum {F}_{x}}{{F}_{\mathrm{R}}^{\prime }} = {0.3283}，\;\cos \left( {{F}_{\mathrm{R}}^{\prime }， j}\right) = \frac{\sum {F}_{y}}{{F}_{\mathrm{R}}^{\prime }} = - {0.9446}

则有

\angle \left( {{F}_{\mathrm{R}}^{\prime }， i}\right) = \pm {70.84}^{ \circ }，\;\angle \left( {{F}_{\mathrm{R}}^{\prime }， j}\right) = {180}^{ \circ } \pm {19.16}^{ \circ }

故主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 在第四象限内，与 x 轴的夹角为 - {70.84}^{ \circ } 。

力系对点 O 的主矩为

{M}_{0} = \sum {M}_{0}\left( {F}_{i}\right) = - 3\mathrm{\;m} \cdot {F}_{1} - {1.5}\mathrm{\;m} \cdot {P}_{1} - {3.9}\mathrm{\;m} \cdot {P}_{2} = - {2355}\mathrm{{kN}} \cdot \mathrm{m}

(2)合力 {\mathbf{F}}_{\mathrm{R}} 的大小和方向与主矢 {\mathbf{F}}_{\mathrm{R}}^{\prime } 相同。其作用线位置的 x 值依据合力矩定理求得(图 24c)，由于

{M}_{o}\left( {\mathbf{F}}_{\mathrm{R}x}\right) = 0

{M}_{O} = {M}_{O}\left( {F}_{\mathrm{R}}\right) = {M}_{O}\left( {F}_{\mathrm{{Rx}}}\right) + {M}_{O}\left( {F}_{\mathrm{{Ry}}}\right) = {F}_{\mathrm{{Ry}}} \cdot x

解得

x = \frac{{M}_{0}}{{F}_{\mathrm{{Ry}}}} = \frac{{2355}\mathrm{{kN}} \cdot \mathrm{m}}{{670.1}\mathrm{{kN}}} = {3.514}\mathrm{\;m}

(3)设合力作用线上任一点的坐标为(x， y)，将合力作用于此点，则合力 {\mathbf{F}}_{\mathrm{R}} 对坐标原点的力矩的解析表达式为

{M}_{O} = {M}_{O}\left( {F}_{\mathrm{R}}\right) = x{F}_{\mathrm{R}y} - y{F}_{\mathrm{R}x}

将已求得的 {M}_{0}\text{、}{F}_{Rx}\text{、}{F}_{Ry} 的代数值代入上式，得合力作用线方程为

{670.1x} + {232.9y} - {2355} = 0

4 平面任意力系的平衡条件和平衡方程

现在讨论静力学中最重要的情形，即平面任意力系的主矢和主矩都等于零的情形:

{\mathbf{F}}_{\mathrm{R}}^{\prime } = \mathbf{0}，\;{M}_{o} = 0 \tag{20}

这表明该力系与零力系等效，因此，该力系必为平衡力系，且式 (20) 是平面任意力系平衡的充分必要条件。

于是， 平面任意力系平衡的必要和充分条件是: 力系的主矢和对于任一点的主矩都等于零。

这些平衡条件可用解析式表示。由式 (17) 和式 (18) 可得

\sum {F}_{x} = 0，\;\sum {F}_{y} = 0，\;\sum {M}_{0}\left( {F}_{i}\right) = 0 \tag{21}

由此可得结论: 平面任意力系平衡的解析条件是所有各力在两个任选的坐标轴上的投影的代数和分别等于零， 各力对于任意一点的力矩的代数和也等于零。式 (21) 称为平面任意力系的平衡方程。

式 (21) 是三个独立的方程， 可以求解三个未知量。

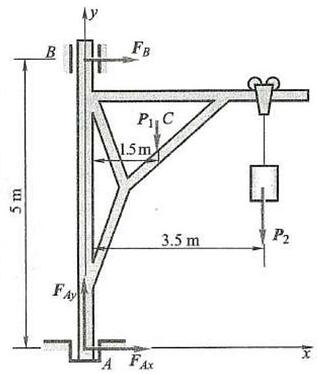
例 7 起重机的重量 {P}_{1} = {10}\mathrm{{kN}} ，可绕铅垂轴 {AB} 转动; 起重机的挂钩上挂一重量为 {P}_{2} = {40}\mathrm{{kN}} 的重物，如图 25 所示。起重机的重心 C 到转动轴的距离为 {1.5}\mathrm{\;m} ，其他尺寸如图所示。求在止推轴承 A 和径向轴承 B 处的约束力。

图 25

解: 以起重机为研究对象，它所受的主动力有 {\mathbf{P}}_{1} 和 {\mathbf{P}}_{2} ，由于对称性，约束力和主动力都位于同一平面内。止推轴承 A 处有两个约束力 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay} ，轴承 B 处只有一个与转轴垂直的约束力 {\mathbf{F}}_{B} ，约束力方向设为如图 25 所示。

建立坐标系如图所示， 列平面任意力系的平衡方程， 即

\sum {F}_{x} = 0，\;{F}_{Ax} + {F}_{B} = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - {P}_{1} - {P}_{2} = 0

\sum {M}_{A}\left( F\right) = 0，\; - 5\mathrm{\;m} \cdot {F}_{B} - {1.5}\mathrm{\;m} \cdot {P}_{1} - {3.5}\mathrm{\;m} \cdot {P}_{2} = 0

求解以上方程， 得

{F}_{B} = - {31}\mathrm{{kN}}，\;{F}_{Ax} = {31}\mathrm{{kN}}，\;{F}_{Ay} = {50}\mathrm{{kN}}

图 26

{F}_{B} 为负值，说明其方向与假设方向相反，即应指向左。

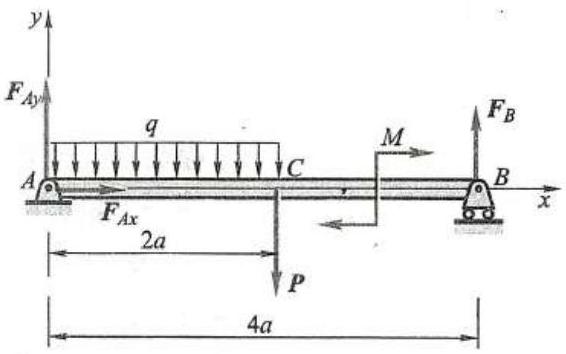
例 8 图 26 所示的均质水平横梁 {AB}， A 端为固定铰链支座， B 端为滚动支座。 梁长为 {4a} ，重为 P 。在梁的 {AC} 段上受均布载荷 q 作用，在梁的 {BC} 段上受力偶矩为 M = {Pa} 的力偶作用。求支座 A 和 B 处的约束力。

解: 选取梁 {AB} 为研究对象。它所受的主动力有: 均布载荷 q 、重力 P 和力偶矩为 M 的力偶。 它所受的约束力有: 铰链 A 的两个分力 {\mathbf{F}}_{Ax} 和 {\mathbf{F}}_{Ay} ，滚动支座 B 处铅垂向上的约束力 {\mathbf{F}}_{B} 。画出其受力图并建立坐标系如图所示， 列出平衡方程:

\sum {F}_{x} = 0，\;{F}_{Ax} = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - {2a} \cdot q - P + {F}_{B} = 0

\sum {M}_{A}\left( F\right) = 0，\;{F}_{B} \cdot {4a} - P \cdot {2a} - {2aq} \cdot a - M = 0

解得

{F}_{Ax} = 0，\;{F}_{B} = \frac{3}{4}P + \frac{1}{2}{qa}，\;{F}_{Ay} = \frac{P}{4} + \frac{3}{2}{qa}

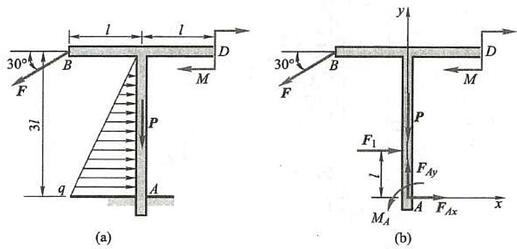
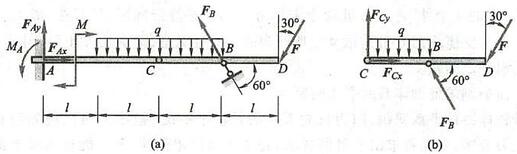
例 9 自重为 P = {100}\mathrm{{kN}} 的 \mathrm{T} 字形刚架 {ABD} ，置于铅垂面内， l = 1\mathrm{\;m} ，载荷如图 27a 所示， M = {20}\mathrm{{kN}} \cdot \mathrm{m}， F = {400}\mathrm{{kN}}， q = {20}\mathrm{{kN}}/\mathrm{m} 。求固定端 A 处的约束力。

图 27

解: 取 \mathrm{T} 字形刚架为研究对象，其上除受主动力外，还受固定端 A 处的约束力 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay} 和约束力偶 {M}_{A} 作用。线性分布载荷用一集中力 {F}_{1} 等效替代，其大小为 {F}_{1} = \frac{3}{2}{ql} ，刚架受力图如图 27b所示。

按图示坐标系，列平衡方程:

\sum {F}_{x} = 0，\;{F}_{Ax} + {F}_{1} - F\cos {30}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - P - F\sin {30}^{ \circ } = 0

\sum {M}_{A}\left( F\right) = 0，\;{M}_{A} - M - {F}_{1} \cdot l + F\cos {30}^{ \circ } \cdot {3l} + F\sin {30}^{ \circ } \cdot l = 0

解方程， 求得

{F}_{Ax} = {316.4}\mathrm{{kN}}，\;{F}_{Ay} = {300}\mathrm{{kN}}，\;{M}_{A} = - {1188}\mathrm{{kN}} \cdot \mathrm{m}

负号说明图中所设方向与实际情况相反，即 {M}_{A} 应为顺时针转向。

平面任意力系的平衡方程还有其他两组形式。

(1)三个平衡方程中有两个力矩方程和一个投影方程，即

\sum {M}_{A}\left( \mathbf{F}\right) = 0，\;\sum {M}_{B}\left( \mathbf{F}\right) = 0，\;\sum {F}_{x} = 0 \tag{22}

其中， x 轴不得垂直于 A\text{、}B 两点的连线。

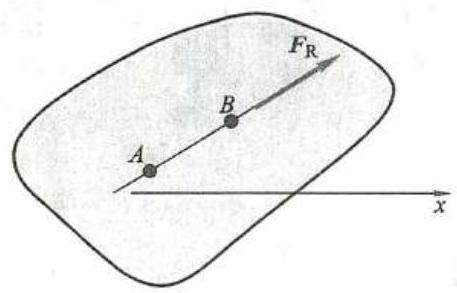
为什么上述形式的平衡方程也能满足力系平衡的必要和充分条件呢? 这是因为，如果力系对点 A 的主矩等于零，则这个力系不可能简化为一个力偶。但可能有两种情形: 这个力系或者是简化为经过点 A 的一个力，或者平衡。如果力系对另一点 B 的主矩也同时为零，则这个力系或有一合力沿 A\text{、}B 两点的连线，或者平衡 (图 28)。如果再加上 \sum {F}_{x} = 0 ，那么力系如有合力，则此合力必与 x 轴垂直。式 (22)的附加条件(x 轴不得垂直于直线 {AB} )完全排除了力系简化为一个合力的可能性， 故所研究的力系必为平衡力系。

(2)平衡方程为三个力矩方程， 即

\sum {M}_{A}\left( \mathbf{F}\right) = 0，\;\sum {M}_{B}\left( \mathbf{F}\right) = 0，\;\sum {M}_{C}\left( \mathbf{F}\right) = 0 \tag{23}

其中， A\text{、}B\text{、}C 三点不得共线。

上述三组方程式 (21)、式 (22) 和式 (23)，究竟选用哪一组方程，须根据具体条件确定。对于受平面任意力系作用的单个刚体的平衡问题， 只可以写出 3 个独立的平衡方程， 求解 3 个未知量。任何第 4 个方程只是前 3 个方程的线性组合，因而不是独立的。

当平面力系中各力的作用线互相平行时， 称之为平面平行力系， 它是平面任意力系的一种特殊情形。

如图 29 所示，设物体受平面平行力系 {\mathbf{F}}_{1}，{\mathbf{F}}_{2}，\cdots ，{\mathbf{F}}_{n} 的作用。如选取 x 轴与各力垂直，则不论力系是否平衡，每一个力在 x 轴上的投影恒等于零，即 \sum {F}_{x} \equiv 0 。 于是， 平面平行力系的独立平衡方程的数目只有两个， 即

\left. \begin{array}{l} \sum {F}_{y} = 0 \\ \sum {M}_{O}\left( \mathbf{F}\right) = 0 \end{array}\right\} \tag{24}

图 28

图 29

容易看出，当 x 、 y 轴取其他方向时，独立的平衡方程仍为两个，可以求解两个未知量。

平面平行力系的平衡方程， 也可用两个力矩方程的形式， 即

\sum {M}_{A}\left( \mathbf{F}\right) = 0，\;\sum {M}_{B}\left( \mathbf{F}\right) = 0 \tag{25}

其中， A\text{、}B 两点连线不与力的作用线平行。

5 物体系的平衡 - 静定和超静定问题

工程中，如组合构架、三铰拱等结构，都是由几个物体组成的系统。当物体系平衡时， 组成该系统的每一个物体都处于平衡状态， 因此， 对于每一个受平面任意力系作用的物体，均可写出 3 个平衡方程。如物体系由 n 个物体组成，则共有 {3n} 个独立方程。如系统中有的物体受平面汇交力系或平面平行力系作用时， 则系统的平衡方程数目相应减少。当系统中的未知量数目等于独立平衡方程的数目时， 则所有未知数都能由平衡方程求出， 这样的问题被称为静定问题。显然前面列举的各例都是静定问题。在工程实际中， 有时为了提高结构的刚度和坚固性， 常常增加约束， 因而使这些结构的未知量的数目多于平衡方程的数目， 未知量就不能全部由平衡方程求出， 这样的问题被称为超静定问题。对于超静定问题， 必须考虑物体因受力作用而产生的变形， 加列某些补充方程后， 才能使方程的数目等于未知量的数目。超静定问题已超出刚体静力学的范围，须在材料力学和结构力学中研究。

下面举出一些静定和超静定问题的例子。

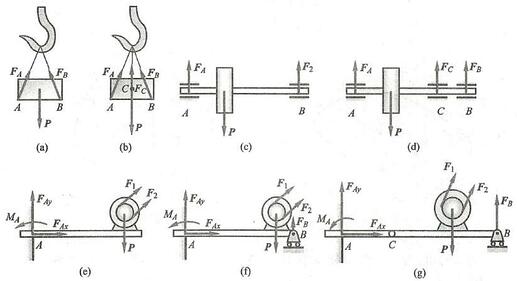
用两根绳子悬挂一重物，如图 30a 所示，未知的约束力有两个，而重物受平面汇交力系作用，有两个独立平衡方程，因此为静定问题。若用 3 根位于同一平面内的绳子悬挂重物，且力的作用线在平面内交于一点，如图 30b 所示，未知约束力有 3 个，而独立平衡方程为两个，因此是超静定问题。

图 30

用两个径向轴承支承一根轴，如图 30c 所示，未知约束力为两个，轴受平面平行力系作用， 有两个独立平衡方程， 是静定问题。若用 3 个径向轴承支承， 如图 30d所示， 则未知的约束力为 3 个， 而独立平衡方程为两个， 因此是超静定问题。

图 30e 所示系统受平面任意力系作用，有 3 个独立平衡方程，有 3 个未知数， 因此是静定问题。图 30f 所示系统受平面任意力系作用， 有 3 个独立平衡方程， 有 4 个未知数， 因此是超静定问题。

图 30g 所示的梁由两部分组成，每部分有 3 个独立平衡方程，共有 6 个未知数 (除图示的 4 个外，还有 C 处两个未知力)，因此是静定问题，但若在 {AB} 之间再加一个滚动支座或把 B 处的滚动支座改为固定铰链支座，则系统共有 7 个未知数， 因此是超静定问题。

下面举例求解物体系的平衡问题。

对物体系的平衡问题，因为首先看到的是整个系统 (整体)， 所以应先对整体进行受力分析， 看能否求出题目所要求， 若能求出则用整体， 若不能求出或不能全部求出，则应考虑拆开整体进行分析。

例 10 在图 31a中，已知重力 P，{DC} = {CE} = {CA} = {CB} = {2l} ，定滑轮半径为 R ，动滑轮半径为 r ，且 R = {2r} = l，\theta = {45}^{ \circ } 。求支座 A\text{、}E 的约束力与杆 {BD} 所受的力。

图 31

解: 先取整体为研究对象， 其受力图如图 31b 所示， 整体有 3 个未知量， 有 3 个独立平衡方程。列平衡方程:

\sum {M}_{E}\left( \mathbf{F}\right) = 0，\;{F}_{A} \cdot 2\sqrt{2}l + P \cdot \frac{5}{2}l = 0

\sum {F}_{x} = 0，\;{F}_{A}\cos {45}^{ \circ } + {F}_{Ex} = 0

\sum {F}_{y} = 0，\;{F}_{A}\sin {45}^{ \circ } + {F}_{Ey} - P = 0

分别解得

{F}_{A} = \frac{-5\sqrt{2}}{8}P，\;{F}_{Ex} = \frac{5P}{8}，\;{F}_{Ey} = \frac{13P}{8}

为求杆 {BD} 所受的力，应取包含此力的物体或系统为研究对象，取杆 {DCE} ，画出其受力图如图 31c 所示，此力系为平面任意力系，可列 3 个独立的平衡方程，未知量为 {F}_{DB}\text{、}{F}_{Cx} 和 {F}_{Cy} ，可求解。因只求杆 {BD} 受力，由对点 C 的一个力矩方程可求。列平衡方程:

\sum {M}_{C}\left( F\right) = 0，\;{F}_{DB}\cos {45}^{ \circ } \cdot {2l} + {F}_{K} \cdot l - {F}_{Ex} \cdot {2l} = 0

解得

{F}_{DB} = \frac{3\sqrt{2}P}{8}

例 11 图 32a 所示不计自重的组合梁，由 {AC} 和 {CD} 在 C 处铰接而成。已知: F = {20}\mathrm{{kN}} ，均布载荷 q = {10}\mathrm{{kN}}/\mathrm{m}， M = {20}\mathrm{{kN}} \cdot \mathrm{m}， l = 1\mathrm{\;m} 。求固定端 A 与滚动支座 B 的约束力。

图 32

解: 先取整体为研究对象，可看出有 4 个未知力 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay}\text{、}{\mathbf{M}}_{A} 与 {\mathbf{F}}_{B} ，受力如图 32a 所示， 但整体只有 3 个独立平衡方程，不能求解。因此，先取梁 {CD} 为研究对象，其受力图如图 32b 所示，由对点 C 的力矩方程可求出约束力 {F}_{B} ，列对点 C 的力矩方程:

\sum {M}_{C}\left( \mathbf{F}\right) = 0，\;{F}_{B}\sin {60}^{ \circ } \cdot l - F\cos {30}^{ \circ } \cdot {2l} - {ql} \cdot \frac{l}{2} = 0

解得

{F}_{B} = {45.77}\mathrm{{kN}}

对整体列 3 个平衡方程， 有

\sum {F}_{x} = 0，\;{F}_{Ax} - {F}_{B}\cos {60}^{ \circ } - F\sin {30}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{Ay} + {F}_{B}\sin {60}^{ \circ } - {2ql} - F\cos {30}^{ \circ } = 0

\sum {M}_{A}\left( F\right) = 0，\;{M}_{A} - M - {2ql} \cdot {2l} + {F}_{B}\sin {60}^{ \circ } \cdot {3l} - F\cos {30}^{ \circ } \cdot {4l} = 0

分别解得

{F}_{Ax} = {32.89}\mathrm{{kN}}，\;{F}_{Ay} = - {2.32}\mathrm{{kN}}，\;{M}_{A} = {10.37}\mathrm{{kN}} \cdot \mathrm{m}

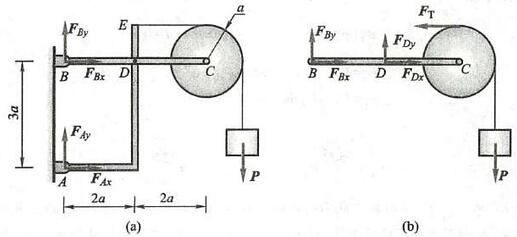
例 12 不计图 33a 所示结构各构件自重，已知尺寸 a 、重力 \mathbf{P} 。求支座 A 、 B 处的约束力。

图 33

解: 本题只讲解题思路， 不具体求解。

本题整体受力图如图 33a 所示，共有 4 个未知力，而独立平衡方程只有 3 个，不能求出 4 个未知力。但可看出，由 \sum {M}_{A} = 0 ，可求出未知力 {F}_{Bx} 。同理，由 \sum {M}_{B} = 0 ，可求出未知力 {F}_{Ax} 。但在求出一个水平约束力时，用 \sum {F}_{x} = 0 求出另一个水平约束力更方便些。这样，虽然分析整体不能求出全部未知量， 但是可以得到其中的一个或两个未知量， 再接着往下分析就相对容易了， 这种情况在求解静力学物体系的平衡问题中很常见。

取水平杆与轮为一体，其受力图如图 33b 所示。由 \sum {M}_{D} = 0 可求出未知力 {F}_{By} ，此时对整体分析，由 \sum {F}_{y} = 0 可求出 {F}_{Ay} 。

当然，去掉轮只取水平杆， C 处铅垂方向的力就是重力 \mathbf{P} ，由 \sum {M}_{D} = 0 求解更方便。

也可取杆 {ADE} (受力图略)，由 \sum {M}_{D} = 0 ，可求出未知力 {F}_{Ay} ，此时对整体分析，由 \sum {F}_{y} = 0 可求出 {F}_{By} 。

这样， 此题列出 4 个一元一次方程求解出了 4 个未知力。

答案给出如下:

{F}_{Ax} = \frac{5}{3}P，\;{F}_{Bx} = - \frac{5}{3}P，\;{F}_{Ay} = {2P}，\;{F}_{By} = P

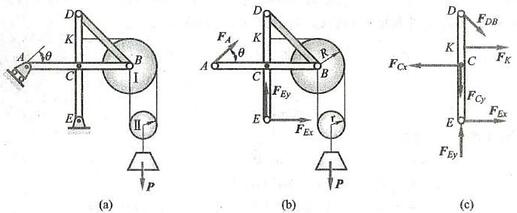
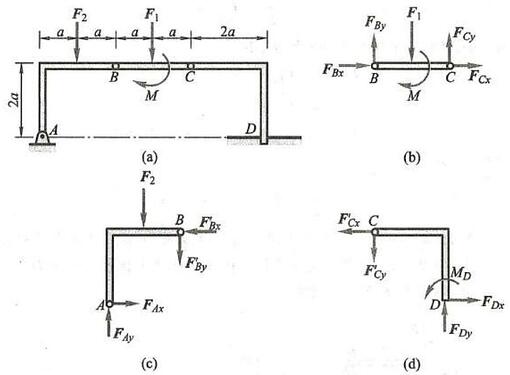
例 13 不计图 34a 所示结构各构件自重，已知 a， M = {Fa}，{F}_{1} = {F}_{2} = F 。求支座 A\text{、}D 处的约束力。

图 34

解: 首先取整体，共有 5 个未知约束力，分别为 A 处两个约束力， D 处 3 个约束力。若先从整体考虑，则一个约束力也求不出。为此，应先考虑把结构拆开，分别画出构件 {BC}\text{、}{AB}\text{、}{CD} 的受力图，如图 34b、c、d 所示。从图 b 可看出，由 \sum {M}_{C} = 0 可求出 {F}_{By} ，从而由图 c 列 3 个方程可求出 A 处两个约束力与 B 处水平方向约束力。再由图 \mathrm{b} 列两个方程可求出 C 处两个约束力，最后对图 d 列 3 个方程可求出 D 处 3 个约束力。本题就按此思路求解。

先取构件 {BC} ，画出其受力图如图 34b 所示，由

\sum {M}_{C} = 0，\; - {F}_{By} \cdot {2a} + {F}_{1} \cdot a - M = 0

解得

{F}_{By} = 0

取构件 {AB} ，其受力图如图 34c 所示，由

\sum {M}_{A} = 0，\;{F}_{Bx}^{\prime } \cdot {2a} - {F}_{2} \cdot a - {F}_{By}^{\prime } \cdot {2a} = 0

解得

{F}_{Bx}^{\prime } = \frac{F}{2}

由

\sum {F}_{x} = 0，\;{F}_{Ax} - {F}_{Bx}^{\prime } = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - {F}_{By}^{\prime } - {F}_{2} = 0

解得 A 处约束力为

{F}_{Ax} = \frac{F}{2}，\;{F}_{Ay} = F

对构件 {BC} (图 34b)，由

\sum {F}_{x} = 0，\;{F}_{Bx} + {F}_{Cx}^{\prime } = 0

\sum {F}_{y} = 0，\;{F}_{By} - {F}_{1} + {F}_{Cy} = 0

解得

{F}_{{C}_{x}} = - \frac{F}{2}，\;{F}_{{C}_{y}} = F

最后取构件 {CD} ，其受力图如图 34d 所示，由

\sum {F}_{x} = 0，\;{F}_{Dx} - {F}_{Cx}^{\prime } = 0

\sum {F}_{y} = 0，\;{F}_{Dy} - {F}_{Cy}^{\prime } = 0

\sum {M}_{D} = 0，\;{M}_{D} + {F}_{{C}_{Y}}^{\prime } \cdot {2a} + {F}_{{C}_{X}}^{\prime } \cdot {2a} = 0

分别解得 D 处约束力为

{F}_{Dx} = - \frac{F}{2}，\;{F}_{Dy} = F，\;{M}_{D} = - {Fa}

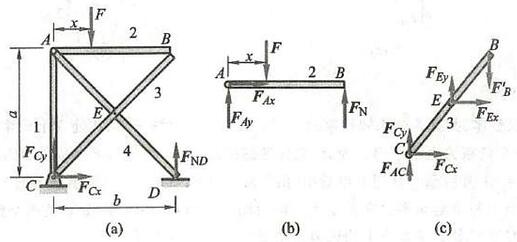
例 14 编号为 1、2、3、4 的四根杆件组成平面结构，其中 A\text{、}C\text{、}E 为光滑铰链， B\text{、}D 为光滑接触， E 为中点，如图 35a 所示。各杆自重不计。在水平杆 2 上作用有铅垂力 F ，尺寸 a 、 b 已知。证明杆 1 受压力，大小为 F 且与 x 无关。

图 35

解: 此题看似为证明题， 实际是求杆 1 的受力。

先分析整体，受力图如图 35a 所示，3 个未知量可列 3 个方程求出。列平衡方程:

\sum {F}_{x} = 0，\;{F}_{Cx} = 0

\sum {F}_{y} = 0，\;{F}_{{C}_{y}} + {F}_{ND} - F = 0

\sum {M}_{C} = 0，\;{F}_{ND} \cdot b - F \cdot x = 0

解得

{F}_{Cs} = 0，\;{F}_{Cy} = F - \frac{x}{b}F，\;{F}_{ND} = \frac{x}{b}F

再来分析单个构件。要求杆 1 的受力，因杆 1 为二力杆，故一般不单独对其分析(请读者思考这是为什么)， 其受力需通过其他构件加以体现。为此， 首先分析杆 2， 要体现杆 1 的受力， 则在点 A 需要带着销，这样点 A 受到来自杆 1 和杆 4 的 3 个未知约束力作用，再加上 B 处杆 3 的约束力，一共有 4 个未知量，无法全部求解。因此，单独分析杆 2 不可行。但分析杆 2 可得到杆 3 与杆 2 在 B 处的作用力，此时 A 处不需要带销。为此，先取杆 2， A 处不带销，受力如图 35b 所示。仅计算 {F}_{B} 的大小，对点 A 列力矩方程即可求解。由

\sum {M}_{A} = 0，\;{F}_{B} \cdot b - F \cdot x = 0

解得

{F}_{B} = \frac{x}{b}F

分析杆 4 与分析杆 2 的情况相似，点 A 需带着销才能体现杆 1 的作用力，但如此一来，未知量不可全部求解。现分析杆 3，为了体现杆 1 的作用力，点 C 需带着销。点 C 的受力为来自支座的约束力 {\mathbf{F}}_{Cx} 、 {\mathbf{F}}_{Cy} (分析整体时已得到)和杆 1 的作用力 {\mathbf{F}}_{AC} 。杆 3 的受力图如图 35c 所示， {F}_{B}^{\prime } 已知，共有 3 个未知量，列 3 个平衡方程可求。为了求 {F}_{AC} ，直接对点 E 列力矩方程:

\sum {M}_{E} = 0，\;{F}_{Cx} \cdot \frac{a}{2} - \left( {{F}_{Cy} + {F}_{AC}}\right) \cdot \frac{b}{2} - {F}_{B}^{\prime } \cdot \frac{b}{2} = 0

得

{F}_{AC} = - F

即杆 1 受压力，大小为 F 且与 x 无关。

在某些情况下， 可能取整体或任何一个分离体单独分析时都不能求出任何未知量， 此时需要充分利用未知量之间的关系将它们联立起来求解。

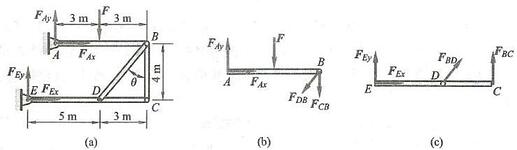
例 15 构架尺寸如图 36a 所示，不计各杆件自重，载荷 F = {60}\mathrm{{kN}} 。求铰链 A\text{、}E 的约束力及杆 {BD}\text{、}{BC} 的内力。

图 36

解:先分析整体，受力图如图 36a 所示，无法全部求出 4 个未知量，需要取分离体进行分析。杆 {BD}\text{、}{BC} 为二力杆，一般很少单独进行分析。

取杆 {AB} ，点 B 带销，假设两二力杆均受拉力，则其受力图如图 36b 所示，仍然是 4 个未知量，不可全部求出。杆 {EC} 的受力情况分析与杆 {AB} 相似，不可全部求出 4 个未知量。为此，对杆 {AB} 先列出 3 个平衡方程:

\sum {F}_{x} = 0，\;{F}_{Ax} - {F}_{DB}\sin \theta = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - F - {F}_{DB}\cos \theta - {F}_{CB} = 0

\sum {M}_{A} = 0，\; - F \cdot 3\mathrm{\;m} - {F}_{DB}\cos \theta \cdot 6\mathrm{\;m} - {F}_{CB} \cdot 6\mathrm{\;m} = 0

取杆 {EC} ，其受力图如图 36c 所示，类似地列出 3 个平衡方程:

\sum {F}_{x} = 0，\;{F}_{Ex} + {F}_{BD}\sin \theta = 0

\sum {F}_{y} = 0，\;{F}_{Ey} + {F}_{BD}\cos \theta + {F}_{BC} = 0

\sum {M}_{E} = 0，\;{F}_{BD}\cos \theta \cdot 5\mathrm{\;m} + {F}_{BC} \cdot 8\mathrm{\;m} = 0

现有 6 个独立的方程，可解 6 个未知量。考虑到 {F}_{BD} = {F}_{DB}，{F}_{BC} = {F}_{CB} ，本质上只有 {F}_{Ax}\text{、}{F}_{Ay}\text{、}{F}_{Ex} 、 {F}_{Ey} 、 {F}_{DB} 、 {F}_{BC}6 个未知量，可以完全求解。代入 \cos \theta = 4/5，\sin \theta = 3/5 ，得

{F}_{Ax} = - {60}\mathrm{{kN}}，\;{F}_{Ay} = {30}\mathrm{{kN}}

{F}_{Ex} = {60}\mathrm{{kN}}，\;{F}_{Ey} = {30}\mathrm{{kN}}

{F}_{BD} = - {100}\mathrm{{kN}}，\;{F}_{BC} = {50}\mathrm{{kN}}

6 平面简单桁架的内力计算

桁架的优点是杆件主要承受拉力或压力， 可以充分利用结构的性能， 节约材料， 减轻结构的重量。为了简化桁架的计算， 工程实际中采用以下几个假设:

(1)桁架中的各杆件均是直杆，各杆件轴线均位于同一平面内，该平面称为桁架的几何平面，且各杆轴线通过铰链 (节点) 中心。

(2)桁架中的各杆件在两端均为光滑铰链连接。

(3)桁架所受的力(载荷)都作用在节点上，而且在桁架的几何平面内。

(4)桁架杆件的重量略去不计，或平均分配在杆件两端的节点上，也位于桁架的几何平面内。

实际的桁架， 当然与上述假设有差别， 如桁架的节点不一定是铰接的， 杆件的中心线也不可能是绝对直的。但上述假设不仅能够简化计算， 而且所得的结果符合工程实际的需要。满足上述简化条件的桁架被称为理想桁架， 其中的杆件均为二力杆。

最简单的平面桁架由 3 根杆和 3 个节点组成，如图 37a 所示的基本三角形部分，就是最简单的桁架。可看出， 每增加一个节点， 最少要增加两根杆。设一任意平面桁架的总杆件数用 m 表示，总节点数用 n 表示，从基本三角形出发，则增加的杆件数和增加的节点数之间的关系为

m - 3 = 2\left( {n - 3}\right)

图 37

得到桁架总杆件数 m 和总节点数 n 之间的关系为

m = {2n} - 3

总杆件数与总节点数满足此关系的平面桁架被称为简单 (静定) 桁架， 若 m > {2n} - 3 ，被称为复杂 (超静定) 桁架，若 m < {2n} - 3 ，则已不是桁架。图 37a 所示为一简单桁架， 图 37b 所示为一复杂桁架。

下面通过例 16 与例 17 介绍两种计算简单桁架杆件内力的方法:节点法和截面法。

• 1. 节点法

对平面简单理想桁架， 考虑其每一个节点， 可看出每个节点都受到一个平面共点力系的作用。为了求出每根杆件的内力， 可以逐个地取节点为研究对象 (当然有先后顺序)， 对每个节点列出两个平衡方程， 由已知力求出全部的杆件内力 (未知力)，这就是节点法。

节点法依次取每一个节点，实际用的是平面汇交力系解题的方法。

例 16 平面简单理想桁架如图 38a 所示。在节点 D 处作用一铅垂集中力 F = {10}\mathrm{{kN}} 。 求桁架中各杆件所受的力。

图 38

解: (1) 求支座约束力

取桁架整体为研究对象，受力图如图 38a 所示。列平衡方程:

\sum {F}_{x} = 0，\;{F}_{Bx} = 0

\sum {M}_{A}\left( F\right) = 0，\;4\mathrm{\;m} \cdot {F}_{By} - 2\mathrm{\;m} \cdot F = 0

\sum {F}_{y} = 0，\;{F}_{Ay} - F + {F}_{By} = 0

分别解得

{F}_{Bx} = 0，\;{F}_{Ay} = {F}_{By} = 5\mathrm{{kN}}

(2)依次取每一个节点为研究对象，计算各杆件内力

假定各杆件均受拉力，各节点受力图如图 38b 所示，为计算方便，最好逐次列出只含两个未知力的节点的平衡方程。

先取节点 A ，杆件的内力 {F}_{1} 和 {F}_{2} 未知。列平衡方程:

\sum {F}_{x} = 0，\;{F}_{2} + {F}_{1}\cos {30}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{Ay} + {F}_{1}\sin {30}^{ \circ } = 0

解得

{F}_{1} = - {10}\mathrm{{kN}}\text{(压力)，}{F}_{2} = {8.66}\mathrm{{kN}}\text{(拉力)}

假定各杆件均受拉力，计算结果为正值，表明杆件受拉力；结果为负，表明杆件受压力。

其次取节点 C ，杆件的内力 {\mathbf{F}}_{3} 和 {\mathbf{F}}_{4} 未知。列平衡方程:

\sum {F}_{x} = 0，\;{F}_{4}\cos {30}^{ \circ } - {F}_{1}^{\prime }\cos {30}^{ \circ } = 0

\sum {F}_{y} = 0，\; - {F}_{3} - \left( {{F}_{1}^{\prime } + {F}_{4}}\right) \sin {30}^{ \circ } = 0

解得

{F}_{3} = {10}\mathrm{{kN}}\text{(拉力)，}{F}_{4} = - {10}\mathrm{{kN}}\text{(压力)}

最后取节点 D ，杆件的内力 {F}_{5} 未知。列平衡方程:

\sum {F}_{s} = 0，\;{F}_{5} - {F}_{2}^{\prime } = 0

解得

{F}_{5} = {8.66}\mathrm{{kN}}\text{(拉力)}

(3)校核计算结果

各杆件内力已求出， 结果是否正确， 可用尚未应用的节点平衡方程校核已得结果。例如， 对此题，对节点 B ，如图 38c 所示，列平衡方程:

\sum {F}_{x} = 0，\;{F}_{Bx} - {F}_{5}^{\prime } - {F}_{4}^{\prime }\cos {30}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{By} + {F}_{4}^{\prime }\sin {30}^{ \circ } = 0

不用求解未知量，把解得的值代入，满足方程等于零，说明计算结果正确。

• 2. 截面法

如只要求计算桁架内某几根杆件所受的内力， 可以适当地选取一截面， 假想把桁架截开， 再考虑其中任一部分的平衡， 求出这些被截杆件的内力， 这就是截面法。

截面法实际采用的是平面任意力系求解的方法， 因为平面任意力系只有 3 个独立的平衡方程， 所以截断 (暴露出未知内力) 的杆件一般不应超过 3 根。

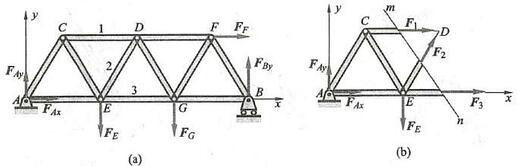
例 17 图39a所示平面桁架，各杆件的长度都等于 1\mathrm{\;m} 。在节点 E\text{、}G\text{、}F 上分别作用铅垂载荷与水平载荷 {F}_{E} = {10}\mathrm{{kN}}，{F}_{C} = 7\mathrm{{kN}}，{F}_{F} = 5\mathrm{{kN}} 。求杆 1\text{、}2\text{、}3 的内力。

解: 首先取整体，求出支座 A 处的约束力，其受力图如图 39a 所示，列平衡方程:

\sum {F}_{x} = 0，\;{F}_{Ax} + {F}_{F} = 0

\sum {M}_{B}\left( F\right) = 0，\; - 3\mathrm{\;m} \cdot {F}_{Ay} + 2\mathrm{\;m} \cdot {F}_{E} + 1\mathrm{\;m} \cdot {F}_{G} - {F}_{F} \cdot 1\mathrm{\;m} \cdot \sin {60}^{ \circ } = 0

解得

{F}_{Ax} = - 5\mathrm{{kN}}，\;{F}_{Ay} = {7.557}\mathrm{{kN}}

图 39

为求杆 1\text{、}2\text{、}3 的内力，取截面 m - n 如图 39b 所示，把 3 根杆件断开，选取左边部分画出其受力图如图 39b 所示，列平衡方程:

\sum {M}_{E}\left( \mathbf{F}\right) = 0，\; - {F}_{Ay} \cdot 1\mathrm{\;m} - {F}_{1} \cdot 1\mathrm{\;m} \cdot \sin {60}^{ \circ } = 0

\sum {F}_{y} = 0，\;{F}_{Ay} + {F}_{2}\sin {60}^{ \circ } - {F}_{E} = 0

\sum {F}_{x} = 0，\;{F}_{Ax} + {F}_{1} + {F}_{2}\cos {60}^{ \circ } + {F}_{3} = 0

解得

{F}_{1} = - {8.726}\mathrm{{kN}}\text{(压力)，}{F}_{2} = {2.821}\mathrm{{kN}}\text{(拉力)，}{F}_{3} = {12.32}\mathrm{{kN}}\text{(拉力)}

如选取桁架的右半部为研究对象，可得同样的结果。

同样， 可以用截面截断另外 3 根杆件， 计算其他各杆件的内力， 或用以校核已求得的结果。