1 静力学公理
公理 1 力的平行四边形法则
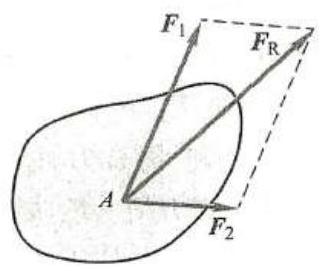
作用在物体上同一点的两个力,可以合成为一个合力,合力的作用点也在该点,合力的大小和方向,由这两个力为边构成的平行四边形的对角线确定,如图 1 所示。合力矢等于这两个力矢的几何和,即
图 1
公理 2 二力平衡条件
作用在同一刚体上的两个力,使刚体保持平衡的必要和充分条件是:这两个力的大小相等,方向相反,且作用在同一直线上。
这条公理表明了作用于刚体上最简单力系平衡时所必须满足的条件。
公理 3 加减平衡力系原理
在任一原有力系上加上或减去任意的平衡力系,与原力系对刚体的作用效果等效。
这条公理是研究力系等效替换的重要依据。
根据上述公理可以导出下列两条推理:
推理 1 力的可传性
作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用。
-
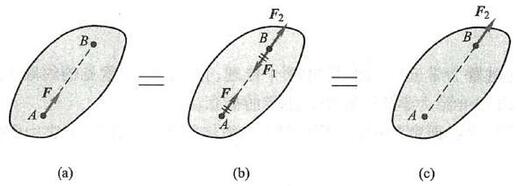
证明: 在刚体上的点 A 作用力 \mathbf{F} ,如图 2a 所示。根据加减平衡力系原理,可在力的作用线上任取一点 B ,并加上两个相互平衡的力 {\mathbf{F}}_{1} 和 {\mathbf{F}}_{2} ,使 \mathbf{F} = {\mathbf{F}}_{2} = - {\mathbf{F}}_{1} ,如图 2b 所示。由于力 \mathbf{F} 和 {\mathbf{F}}_{1} 也是一个平衡力系,故可除去,这样只剩下一个力 {\mathbf{F}}_{2} ,如图 2c 所示,即原来的力 \mathbf{F} 沿其作用线移到了点 B 。
图 2
由此可见,对于刚体来说,力的作用点已由作用线所代替。
因此,作用于刚体上的力的三要素是:力的大小、方向和作用线。
作用于刚体上的力可以沿着其作用线移动,这种矢量称为滑动矢量。
推理 2 三力平衡汇交定理
刚体在三个力作用下平衡,若其中两个力的作用线交于一点,则第三个力的作用线必通过此汇交点,且三个力位于同一平面内。
-
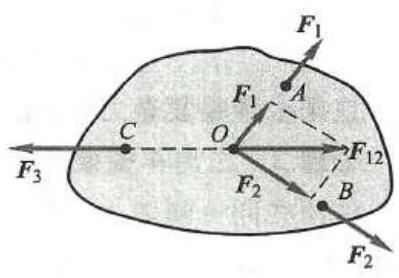
证明: 如图 3 所示,在刚体的 A\text{、}B\text{、}C 三点上,分别作用三个力 {\mathbf{F}}_{1}\text{、}{\mathbf{F}}_{2}\text{、}{\mathbf{F}}_{3} ,且刚体平衡,其中力 {\mathbf{F}}_{1}\text{、}{\mathbf{F}}_{2} 两个力的作用线交于点 O 。根据力的可传性,把力 {\mathbf{F}}_{1}\text{、}{\mathbf{F}}_{2} 移到汇交点 O ,再根据力的平行四边形公理,得合力 {\mathbf{F}}_{12} 。由二力平衡条件,力 {\mathbf{F}}_{3} 、 {\mathbf{F}}_{12} 平衡,则力 {\mathbf{F}}_{3}\text{、}{\mathbf{F}}_{12} 必共线,即力 {\mathbf{F}}_{3} 必通过汇交点 O ,且力 {\mathbf{F}}_{3} 必位于力 {\mathbf{F}}_{1}\text{、}{\mathbf{F}}_{2} 所在的平面内,三力共面,推理 2 得证。
图 3
公理 4 作用和反作用定律
作用力和反作用力总是同时存在,两个力的大小相等,方向相反,沿着同一条直线,分别作用在两个相互作用的物体上。
这条公理描述了作用力与反作用力的关系,在画受力图时要注意该公理的应用。作用和反作用定律与二力平衡条件的描述有相同之处,两个力均是等值、反向、共线,但区别是作用力和反作用力分别作用在相互作用的两个物体上,二力平衡条件中的两个力作用于同一个刚体上。
公理 5 刚化原理:变形体在某一力系作用下处于平衡状态,如将此变形体刚化为刚体,其平衡状态保持不变。
这个公理提供了把变形体看作为刚体模型的条件。
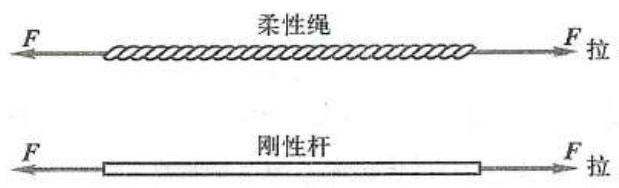
如图 4 所示,绳索在等值、反向、共线的两个拉力作用下处于平衡状态,如将绳索刚化成刚体,其平衡状态保持不变。反之就不一定成立,如刚体在两个等值反向的压力作用下平衡,若将它换成绳索就不能平衡了。
图 4
由此可见,刚体的平衡条件是变形体平衡的必要条件,而非充分条件。
2 约束和约束力
有些物体,如飞行的飞机、炮弹和火箭等,它们在空间的位移不受任何限制。位移不受限制的物体称为自由体。相反,有些物体在空间的位移要受到一定的限制,如机车受铁轨的限制,只能沿轨道运动;电机转子受轴承的限制,只能绕轴线转动;重物由钢索吊住,不能下落;等等。
位移受到限制的物体称为非自由体。对非自由体的某些位移起限制作用的周围物体称为约束。例如,铁轨对于机车,轴承对于电机转子,钢索对于重物等,都是约束。
从力学角度来看,约束对物体的作用,实际上就是力,这种力称为约束力。因此,约束力的方向必与该约束所能够阻碍的位移方向相反。应用这个准则,可以确定约束力的方向或作用线的位置。至于约束力的大小则是未知的。
在静力学问题中,约束力和物体受的其他已知力 (称为主动力) 组成平衡力系,因此,可用平衡条件求出未知的约束力。当主动力改变时,约束力一般也发生改变,因此,约束力是被动的,这也是将约束力之外的力称为主动力的原因。
下面介绍几种在工程中常见的约束类型和确定约束力方向的方法。
2.1 具有光滑接触表面的约束
支持物体的固定面 (图 5a、5b)、啮合齿轮的齿面 (图 6)、机床中的导轨等,当摩擦忽略不计时,都属于这类约束。
这类约束不能限制物体沿约束表面切线方向的位移,只能阻碍物体沿接触表面法线方向并指向约束内部的位移。因此,光滑支承面对物体的约束力,作用在接触点处,方向沿接触表面的公法线,并指向被约束的物体。这种约束力称为法向约束力,通常用 {\mathbf{F}}_{\mathrm{N}} 表示,如图 5 中的 {\mathbf{F}}_{\mathrm{N}A} 、 {\mathbf{F}}_{\mathrm{N}C} 和图 6 中的 {\mathbf{F}}_{\mathrm{N}B} 等。
图 5
图 6
2.2 由柔软的绳索、链条或带等构成的约束
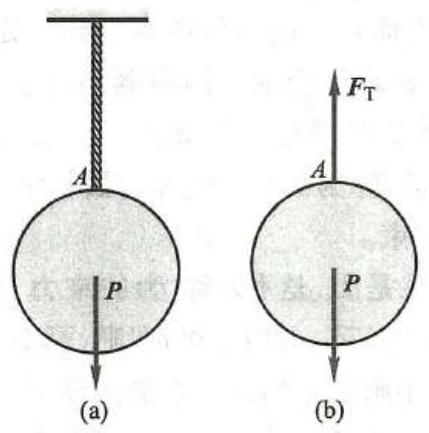
绳索吊住重物,如图 7a 所示。因为柔软的绳索本身只能承受拉力,所以它给物体的约束力也只可能是拉力 (图 7b)。因此,绳索对物体的约束力,作用在接触点,方向沿着绳索背离物体。通常用 \mathbf{F} 或 {\mathbf{F}}_{\mathrm{T}} 表示这类约束力。
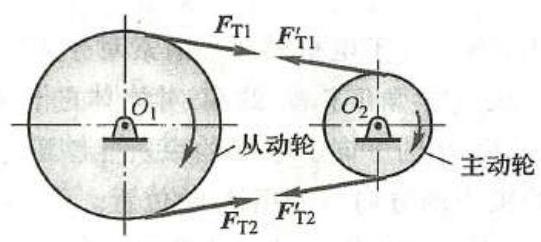
链条或带也都只能承受拉力。当它们绕在轮子上时,对轮子的约束力沿轮缘的切线方向 (图 8)。
一般通称这类约束为柔索约束。
图 7
图 8
3 光滑铰链约束
这类约束有向心轴承、圆柱铰链和固定铰链支座等。
(1) 向心轴承(径向轴承)
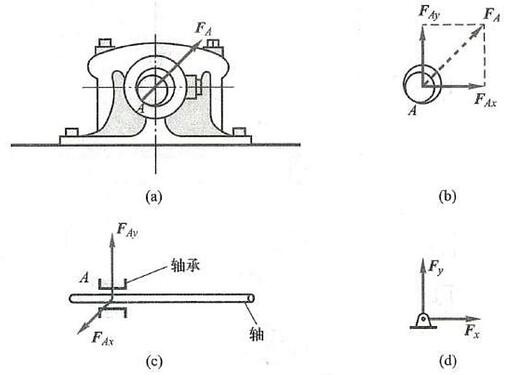
图 9a、9b 所示为轴承装置,可画成如图 9c 所示的简图。
轴可在孔内任意转动,也可沿孔的中心线移动; 但是,轴承阻碍着轴沿径向向外的位移。当轴和轴承在某点 A 光滑接触时,轴承对轴的约束力 {\mathbf{F}}_{A} 作用在接触点 A ,且沿公法线指向轴心 (图 9a)。
图 9
但是,随着轴所受的主动力不同,轴和孔的接触点的位置也随之不同。因此,当主动力尚未确定时,约束力的方向预先不能确定。然而,无论约束力朝向何方,它的作用线必垂直于轴线并通过轴心。这样一个方向不能预先确定的约束力,通常可用通过轴心的两个大小未知的正交分力 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay} 来表示,如图 9b 或 9c 所示,{\mathbf{F}}_{Ax} 、 {\mathbf{F}}_{Ay} 的指向暂可任意假定。
在平面问题中,此类约束一般用图 9d 所示的符号表示。
(2) 圆柱铰链和固定铰链支座
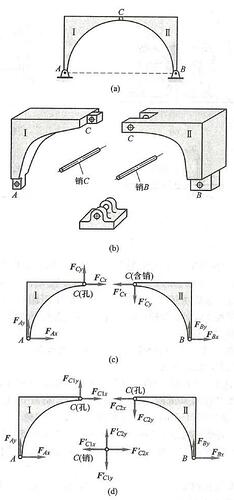
图 10a 所示为一拱形桥示意图,它是由两个拱形构件通过圆柱铰链 C 以及固定铰链支座 A 和 B 连接而成的。圆柱铰链是由销 C 将两个钻有同样大小孔的构件连接在一起而成的 (图 10b),其简图如图 10a 的铰链 C 所示。如果铰链连接中有一个固定在地面或机架上作为支座,则这种约束称为固定铰链支座,简称固定铰支,如图 10b 所示的支座 B ,其简图如图 10a 所示的固定铰链支座 A 和 B 。
在分析铰链 C 处的约束力时,通常把销 C 固连在其中任意一个构件上,如构件 \mathrm{{II}} 上,则构件 \mathrm{I} 、\mathrm{{II}} 互为约束。显然,当忽略摩擦时,构件 \mathrm{{II}} 上的销与构件 \mathrm{I} 的结合,实际上是轴与光滑孔的配合问题。因此,它与轴承具有同样的约束性质,即约束力的作用线不能预先定出,但约束力垂直轴线并通过铰链中心,故也可用两个未知的正交分力 {\mathbf{F}}_{Cx}\text{、}{\mathbf{F}}_{Cy} 和 {\mathbf{F}}_{Cx}^{\prime }\text{、}{\mathbf{F}}_{Cy}^{\prime } 来表示,如图 10c 所示。其中 {\mathbf{F}}_{Cx} 和 {\mathbf{F}}_{Cx}^{\prime },{\mathbf{F}}_{Cy} 和 {\mathbf{F}}_{{c}_{y}}^{\prime } 分别互为作用力与反作用力。
同理,把销固连在 A\text{、}B 支座上,则固定铰支 A\text{、}B 对构件 \mathrm{I}\text{、}\mathrm{{II}} 的约束力分别为 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay} 与 {\mathbf{F}}_{Bx}\text{、}{\mathbf{F}}_{By} ,如图 10c 所示。
图 10
当需要分析销 C 的受力时,可把销 C 分离出来单独研究。这时,销 C 将同时受到构件 \mathrm{I} 、 \mathrm{{II}} 上的孔对它的反作用力。其中 {\mathbf{F}}_{C1x} 与 {\mathbf{F}}_{C1x}^{\prime },{\mathbf{F}}_{C1y} 与 {\mathbf{F}}_{C1y}^{\prime } 为构件 \mathrm{I} 与销 C 的作用力与反作用力; {\mathbf{F}}_{C2x} 与 {\mathbf{F}}_{C2x}^{\prime },{\mathbf{F}}_{C2y} 与 {\mathbf{F}}_{C2y}^{\prime } 为构件 \mathrm{{II}} 与销 C 的作用力与反作用力。销 C 所受到的约束力如图 10d 所示。
当将销 C 与构件 \mathrm{{II}} 固连为一体时,{\mathbf{F}}_{C2x} 与 {\mathbf{F}}_{C2x}^{\prime },{\mathbf{F}}_{C2y} 与 {\mathbf{F}}_{C2y}^{\prime } 为作用在同一刚体上的成对的平衡力,可以消去不画。此时,力的下角不必再区分为 {C1} 和 {C2} ,铰链 C 处的约束力仍如图 10c 所示。
上述三种约束 (向心轴承、圆柱铰链和固定铰链支座),它们的具体结构虽然不同,但是构成约束的性质是相同的,一般通称为铰链约束,通常用图 9d 所示的符号表示。此类约束的特点是只限制两物体径向的相对移动,而不限制两物体绕铰链中心的相对转动与沿轴向的位移。此类约束的约束力一般用两个正交分力来表示,如图 9d 所示。
4 其他约束
(1) 滚动支座
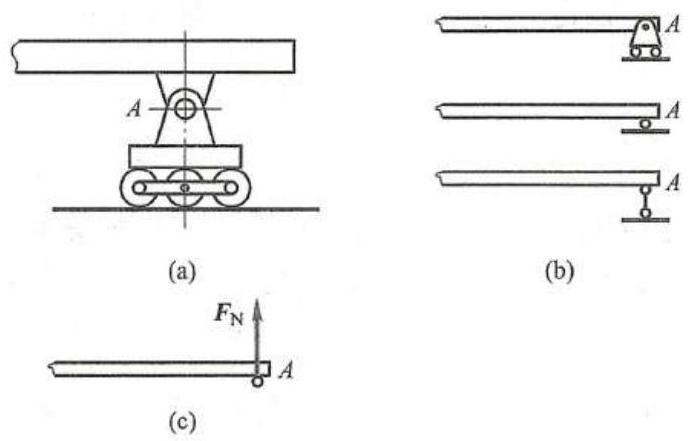
在桥梁、屋架等结构中经常采用滚动支座,这种支座是在固定铰链支座与光滑支承面之间,装有几个滚轴而构成,又称为滚轴支座,如图 11a 所示,其简图如图 11b 所示。它可以沿支承面移动,允许由于温度变化而引起结构跨度的自由伸长或缩短。显然,滚动支座的约束性质与光滑面约束相同,其约束力必垂直于支承面,且通过铰链中心。通常用 {\mathbf{F}}_{\mathrm{N}} 表示其法向约束力,如图 11c 所示。在某些实际工程结构中,滚轴支座除了底面有光滑支承面以外,上面可能还设有盖板,以防支座翘起。 因此,滚动支座的约束力方向也可能指向支承面。
图 11
(2) 球铰链
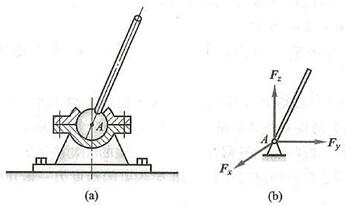
通过球和球壳将两个构件连接在一起的约束称为球铰链,如图 12a 所示。 它使构件的球心不能有任何位移,但构件可绕球心任意转动。若忽略摩擦,其约束力应是通过接触点与球心,但方向不能预先确定的一个空间法向约束力,一般用三个正交分力 {\mathbf{F}}_{x}\text{、}{\mathbf{F}}_{y}\text{、}{\mathbf{F}}_{z} 表示,其简图及约束力如图 12b 所示。
图 12
(3) 止推轴承
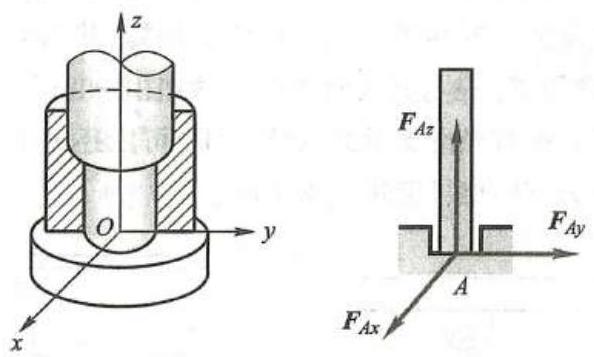
止推轴承与径向轴承不同,它除了能限制轴的径向位移以外,还能限制轴沿轴向的位移。因此,它比径向轴承多一个沿轴向的约束力,即其约束力有三个正交分量 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay}\text{、}{\mathbf{F}}_{Az} 。止推轴承的简图及其约束力如图 13 所示。
图 13
5 物体的受力分析和受力图
在工程实际中,为了求出未知的约束力,需要根据已知力,应用平衡条件求解。 为此,首先要确定构件受了几个力,以及每个力的作用位置和力的作用方向,这种分析过程称为物体的受力分析。
作用在物体上的力可分为两类:一类是主动力,例如,物体的重力、风力、气体压力等,一般是已知的;另一类是约束对物体的约束力,为未知的被动力。
为了清晰地表示物体的受力情况,首先要把需要研究的物体 (称为受力体) 从周围的物体 (称为施力体) 中分离出来,单独画出它的受力简图,这个步骤叫作取研究对象或取分离体。然后,把施力物体对研究对象的作用力 (包括主动力和约束力)全部画出来。这种表示物体受力的简明图形,称为受力图。
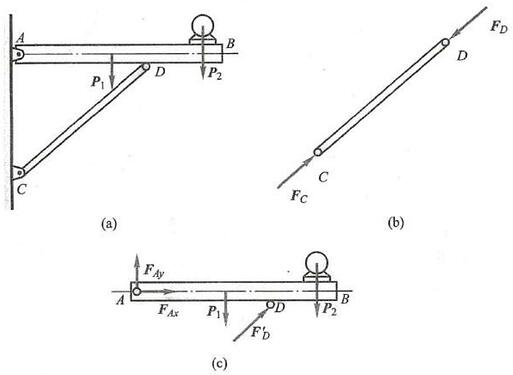
例 1 如图 14a 所示,梁 {AB} 用杆 {CD} 支承,A\text{、}C\text{、}D 三处均为光滑铰链连接。均质梁 {AB} 重为 {P}_{1} ,其上放置一重为 {P}_{2} 的电动机。不计杆 {CD} 的自重,分别画出杆 {CD} 和梁 {AB} (包括电动机) 的受力图。
图 14
解:画受力图一般分三步:取研究对象并画出其简图;画主动力;画约束力。
(1)先画杆 {CD} 的受力图,取杆 {CD} 为研究对象,画出简图(图 14b)。杆 {CD} 上未作用主动力,现画其约束力。由于杆 {CD} 的自重不计,根据光滑铰链的特性,C\text{、}D 处的约束力分别通过铰链 C\text{、}D 的中心,方向暂不确定。考虑到杆 {CD} 只在 {\mathbf{F}}_{C}\text{、}{\mathbf{F}}_{D} 两个力作用下平衡,根据二力平衡条件,这两个力必定沿同一直线,且等值、反向。由此可确定 {\mathbf{F}}_{c} 和 {\mathbf{F}}_{p} 的作用线应沿铰链中心 C 与 D 的连线,由经验判断,此处杆 {CD} 受压力,其受力图如图 14b 所示。一般情况下,{\mathbf{F}}_{c} 与 {\mathbf{F}}_{p} 的指向不能预先判定,可先任意假设杆受拉力或压力。若根据平衡方程求得的力为正值,说明原假设力的指向正确;若为负值,则说明杆实际受力与原假设指向相反。
只在两个力作用下平衡的构件,称为二力构件。由于静力学中所指物体都是刚体,其形状对计算结果没有影响,因此,不论其形状如何,一般均称为二力杆。它所受的两个力必定沿两个力作用点的连线,且等值、反向。二力杆在工程实际中经常遇到,有时也把它作为一种约束,如图 14b 所示。
(2)再画梁 {AB} 的受力图。取梁 {AB} (包括电动机)为研究对象。它受有 {\mathbf{P}}_{1} 、 {\mathbf{P}}_{2} 两个主动力的作用。梁在铰链 D 处受有二力杆 {CD} 给它的反作用力 {\mathbf{F}}_{D}^{\prime } 的作用。梁在 A 处受固定铰支给它的约束力的作用,由于方向未知,可用两个未定的正交分力 {\mathbf{F}}_{Ax} 和 {\mathbf{F}}_{Ay} 表示。梁 {AB} 的受力图如图 14c 所示。
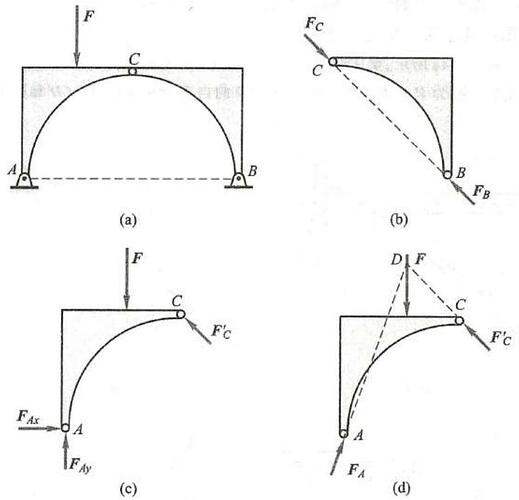
例 2 如图 15a 所示的三铰拱桥,由左、右两拱铰接而成。不计自重及摩擦力,在拱 {AC} 上作用有载荷 F 。试分别画出拱 {AC} 和 {CB} 的受力图。
图 15
解: (1) 先分析拱 {BC} 的受力。由于拱 {BC} 自重不计,且只在 B\text{、}C 两处受到铰链约束,因此,拱 {BC} 为二力构件。在铰链中心 B\text{、}C 处分别受 {\mathbf{F}}_{B}\text{、}{\mathbf{F}}_{C} 两个力的作用,这两个力的方向如图 15b 所示。
(2)再分析拱 {AC} 的受力。取拱 {AC} 为研究对象。由于自重不计,因此,主动力只有载荷 \mathbf{F} 。 拱 {AC} 在铰链 C 处受有拱 {BC} 给它的反作用力 {F}_{C}^{\prime } 的作用,拱在 A 处受有固定铰支给它的约束力 {\mathbf{F}}_{A} 的作用,由于方向未定,可用两个未知的正交分力 {\mathbf{F}}_{Ax} 和 {\mathbf{F}}_{Ay} 代替。拱 {AC} 的受力图如图 15c 所示。
再进一步分析可知,由于拱 {AC} 在 F\text{、}{F}_{C}^{\prime } 及 {F}_{A} 三个力作用下平衡,故可根据三力平衡汇交定理,确定铰链 A 处约束力 {\mathbf{F}}_{A} 的方向。点 D 为力 \mathbf{F} 和 {\mathbf{F}}_{C}^{\prime } 作用线的交点,当拱 {AC} 平衡时,约束力 {\mathbf{F}}_{A} 的作用线必通过点 D (图 15d); 至于 {\mathbf{F}}_{A} 的指向,暂且假定如图所示,以后由平衡条件确定。
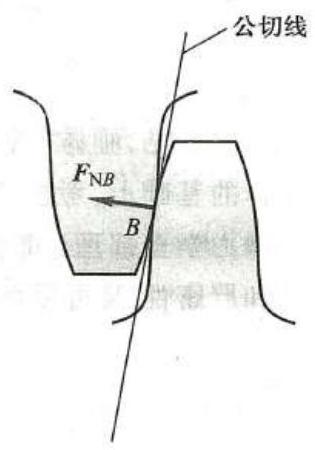
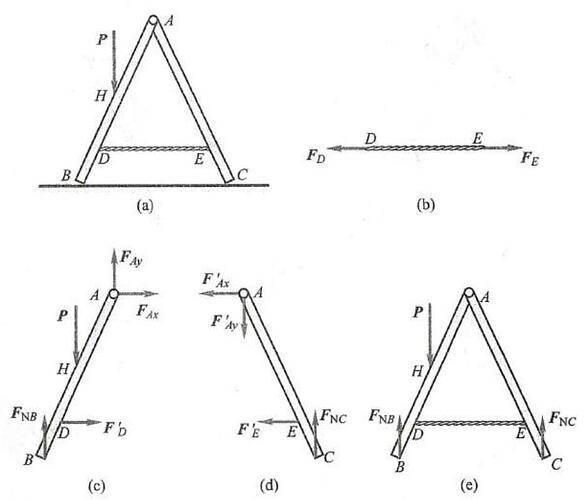
例 3 图 16a 所示为一折叠梯子的示意图,梯子的 {AB}\text{、}{AC} 两部分在点 A 铰接,在 D\text{、}E 两点用绳水平相连。梯子放在光滑水平地板上,自重忽略不计,点 H 处站立一人,其重为 P 。要求分别画出绳子,以及梯子左、右两部分和梯子的整体受力图。
解:(1)绳子为柔索约束,其受力图如图 16b 所示。
(2)先画梯子左边部分 {AB} 的受力图。其在 B 处受到光滑地板对它的法向约束力作用,以 {\mathbf{F}}_{\mathrm{N}B} 表示。在 D 处受到绳子对它的拉力作用,以 {\mathbf{F}}_{D}^{\prime } 表示。在 H 处受到人的重力 \mathbf{P} 的作用。在铰链 A 处,可画为两正交分力,以 {F}_{Ar}\text{、}{F}_{Ay} 表示。梯子左侧的受力图如图 16c 所示。
(3)画梯子右边部分 {AC} 的受力图。其在 C 处受到光滑地板对它的法向约束力作用,以 {\mathbf{F}}_{NC} 表示。在 E 处受到绳子对它的拉力作用,以 {\mathbf{F}}_{E}^{\prime } 表示。在铰链 A 处,受到梯子左边部分对它的反作用力作用,以 {\mathbf{F}}_{Ax}^{\prime }\text{、}{\mathbf{F}}_{Ay}^{\prime } 表示。右边梯子的受力图如图 16d 所示。
图 16
(4)画梯子整体的受力图。在画系统(梯子)的整体受力图时,{AB} 与 {AC} 两部分在 A 处相互有力作用,在点 D 与点 E 绳子对其也有力作用,这些力成对地作用在系统内。系统内各物体之间相互作用的力称为内力,内力是成对出现的,对系统的作用效应相互抵消,因此,在受力图上一般不画出。在受力图上只画出系统以外的物体对系统的作用力,这种力称为外力。这里,人的重力 \mathbf{P} 和地板约束力 {\mathbf{F}}_{NB}\text{、}{\mathbf{F}}_{NC} 是作用于系统上的外力,整个系统 (梯子) 的受力图如图 16e 所示。
当然,内力与外力不是绝对的,例如,当把梯子的两部分拆开时,A 处的作用力和绳子的拉力即为外力,但取整体时,这些力又为内力。因此,内力与外力的区分只有相对某一确定的研究对象才有意义。
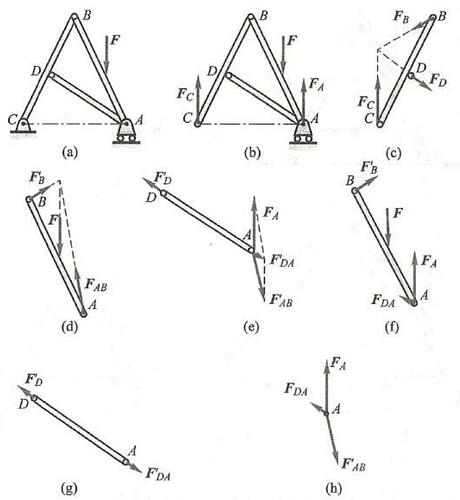
例 4 在图 17a 所示的平面结构中,杆 {AB} 上作用有竖直向下的主动力 \mathbf{F} 。不计各杆的自重与各处的摩擦力,请画出各个构件的受力图与系统整体的受力图。
解:
- 画法 1
(1)先画系统整体的受力图。取整体为研究对象,画出其简图,把整个系统刚化为刚体,主动力为 F 。系统在 A 处受有滚动支座的约束力 {F}_{A} 作用,假设 {F}_{A} 竖直向上; 在 C 处受到固定铰链支座的约束力,一般情况下可以用两个正交分力表示,但此处点 C 的约束力方向可以确定,其必为竖直方向,假设竖直向上,用 {\mathbf{F}}_{c} 表示。这是因为,如果 C 处的约束力不是竖直方向的话,则其作用线必与主动力 \mathbf{F} 相交,根据三力平衡汇交定理,则 \mathbf{A} 处的约束力作用线也必与主动力 \mathbf{F} 相交,这与 {\mathbf{F}}_{A} 沿竖直方向相矛盾。当然,将 C 处的约束力用两个正交分力表示也是可以的。系统整体的受力图如图 17b 所示。
图 17
(2)画杆 {BC} 的受力图。取杆 {BC} 为研究对象,C 处受到支座的约束力 {\mathbf{F}}_{c} 作用,分析整体时已经得到。 D 处受到杆 {AD} 的作用力,因为杆 {AD} 是二力杆,所以 D 处的约束力沿着杆 {AD} 方向,用 {F}_{D} 表示。 B 处通过圆柱铰链与杆 {AB} 连接,受到杆 {AB} 的作用力,可以用两个正交分力表示,但是因为点 C 和点 D 的约束力方向均已知,所以 B 处的约束力方向可由三力平衡汇交定理确定,用 {\mathbf{F}}_{B} 表示。杆 {BC} 的受力图如图 17c 所示。
(3)画杆 {AB} 的受力图。取杆 {AB} 为研究对象,画出其简图。此处需要注意,因为点 A 连接有三个构件 (杆 {AB} 、杆 {AD} 和滚动支座 A ),当铰链连接有三个或三个以上构件 (或受力),将铰链分开时,需要明确销的位置,销放置在不同的位置,受力图是不一样的。选择 A 点不带销。杆 {AB} 首先受主动力 \mathbf{F} 作用,在点 B 受到杆 {BC} 的反作用力 {\mathbf{F}}_{B}^{\prime } 作用;因为点 A 不带销,所以点 A 受到的是来自销的作用力,可用两个正交分力表示,但此处可用三力平衡汇交定理确定其方向,用 {\mathbf{F}}_{AB} 表示。此时,杆 {AB} 的受力图如图 17d 所示。
(4)画杆 {AD} 的受力图。取杆 {AD} 为研究对象,点 A 带销,画出其简图。在点 D 受到杆 {BC} 的反作用力 {\mathbf{F}}_{b}^{\prime } 作用;点 A 带有销,杆 {AD} 与销之间的作用力属于内力,该点所受的外力(约束力) 为销受到的来自杆 {AB} 的反作用力 {F}_{AB}^{\prime } 和滚动支座的作用力。滚动支座的作用力在整体分析时已得到,为 {\mathbf{F}}_{A} 。此时,杆 {AD} 的受力图如图 17e 所示。注意,杆 {AD} 仍为二力杆,只是点 A 受两个力的作用,此二力的合力与 {\mathbf{F}}_{D}^{\prime } 平衡。
以上是将点 A 的销放置在杆 {AD} 上时,各构件受力图的画法。也可将销放置在杆 {AB} 上,此时画出的杆 {AB} 和杆 {AD} 的受力图结果有所不同,但整体和杆 {BC} 的受力图是一样的,此处不再重复。
- 画法 2
(1)画杆 {AB} 的受力图,点 A 带销。同样地,杆 {AB} 首先受主动力 \mathbf{F} 作用,在点 B 受到杆 {BC} 的反作用力 {F}_{B}^{\prime } 作用;因为点 A 带销,所以点 A 与销钉之间的作用力属于内力,点 A 受到的外力为滚动支座的作用力 {\mathbf{F}}_{A} 和杆 {AD} 的作用力。杆 {AD} 为二力杆,所以作用在点 A 的力沿着杆 {AD} 方向,用 {\mathbf{F}}_{DA} 表示。此时,杆 {AB} 的受力图如图 17f 所示。注意,此时对杆 {AB} 不能应用三力平衡汇交定理,虽然点 A 受到的两个力可以合成为一个力,并且其与 \mathbf{F}\text{、}{\mathbf{F}}_{B}^{\prime } 的作用线汇交于一点,但因为这两个力都有各自明确的施力物体,本质上不是一个力,所以不能用合力表示。
(2)画杆 {AD} 的受力图,因为销已置于杆 {AB} 上,所以点 A 不带销。杆 {AD} 为二力杆。同样地,在点 D 受到杆 {BC} 的反作用力 {F}_{D}^{\prime } 作用; 点 A 不带销,所以点 A 受到的是来自销的反作用力 {F}_{DA}^{\prime } ,其与 {F}_{D}^{\prime } 满足二力平衡条件。此时,杆 {AD} 的受力图如图 17g 所示。
也可以将销单独考虑,这样分析杆 {AB} 和杆 {AD} 的受力时就都不需要带销,受力图的画法又有所不同。
- 画法 3
(1)画杆 {AB} 的受力图,点 A 不带销。其受力情况与画法 1 相同,受力图如图 17d 所示。
(2)画杆 {AD} 的受力图,点 A 不带销。其受力情况与画法 2 相同,受力图如图 17g 所示。
(3)此时需要单独分析销 A 的受力。销 A 受到来自杆 {AD} 的作用力 {\mathbf{F}}_{DA} ,杆 {AB} 的作用力 {\mathbf{F}}_{AB}^{\prime } 和滚动支座的约束力 {\mathbf{F}}_{A} ,这三个力相互平衡,其受力图如图 17h 表示。
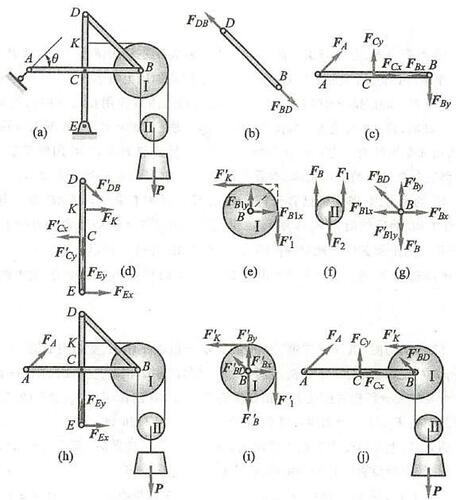
例 5 图 18a 所示的平面构架,由杆 {AB}\text{、}{DE} 与 {DB} 铰接而成。 A 为滚动支座,E 为固定铰链支座。钢丝绳一端拴在 K 处,另一端绕过定滑轮 \mathrm{I} 和动滑轮 \mathrm{{II}} 后拴在销 B 上。物重为 P ,各杆及滑轮的自重不计。
(1)分别画出各杆、各滑轮、销 B 及整个系统的受力图;
(2)画出销 B 与滑轮 \mathrm{I} 一起的受力图;
(3)画出杆 {AB} ,滑轮 I 、II ,钢丝绳和重物作为一个系统时的受力图。
解: (1) 画杆 {BD} 的受力图,取杆 {BD} 为研究对象 ( B 处不带销)。由于杆 {BD} 为二力杆,故在铰链中心 D\text{、}B 处分别受 {\mathbf{F}}_{DB}\text{、}{\mathbf{F}}_{BD} 两个力的作用,其中 {\mathbf{F}}_{BD} 为销给孔 B 的约束力,其受力图如图 18b 所示。
(2)画杆 {AB} 的受力图,取杆 {AB} 为研究对象( B 处仍不带销)。 A 处受有滚动支座的约束力 {\mathbf{F}}_{A} 的作用,C 处为铰链约束,其约束力用两个正交分力 {\mathbf{F}}_{Cx}\text{、}{\mathbf{F}}_{Cy} 表示,B 处受有销给孔 B 的约束力,亦用两个正交分力 {F}_{Bx} 、 {F}_{By} 表示,方向假设如图所示。杆 {AB} 的受力图如图 18c 所示。
(3)画杆 {DE} 的受力图,取杆 {DE} 为研究对象。其上共有 D\text{、}K\text{、}C\text{、}E 四处受力,D 处受二力杆给它的约束力 {F}_{DB}^{\prime } 作用,K 处受钢绳的拉力 {F}_{K} 作用,铰链 C 处受到杆 {AB} 在 C 处对杆 {DE} 的反作用力 {\mathbf{F}}_{Cx}^{\prime } 、 {\mathbf{F}}_{Cy}^{\prime } 作用,E 处为固定铰链支座,其约束力用两个正交分力 {\mathbf{F}}_{Ex} 、 {\mathbf{F}}_{Ey} 表示,杆 {DE} 的受力图如图 18d 所示。
(4)画轮 I 的受力图,取轮 I 为研究对象 (B 处不带销)。在绳和轮的离开处断开,其上受有两段绳的拉力 {F}_{1}^{\prime } 和 {F}_{K}^{\prime } 作用,还有销 B 对孔 B 的约束力 {F}_{B1x}\text{、}{F}_{B1y} 作用,其受力图如图 18e 所示。亦可根据三力平衡汇交定理,确定铰链 B 处约束力的方向,如图中虚线所示。
图 18
(5)画轮 II 的受力图,取轮 II 为研究对象。其上受三段绳的拉力 {\mathbf{F}}_{1} 、 {\mathbf{F}}_{B} 与 {\mathbf{F}}_{2} 作用。轮 II 的受力图如图 18f 所示。
(6)画销 B 的受力图,单独取销 B 为研究对象。它与杆 {DB} 、 {AB} 、轮 \mathrm{I} 与钢丝绳四个物体连接,因此,这四个物体对销都有力作用。二力杆 {DB} 对它的反作用力为 {F}_{BD}^{\prime } ,杆 {AB} 对它的反作用力为 {F}_{Bx}^{\prime }\text{、}{F}_{By}^{\prime } ,轮 \mathrm{I} 给销 B 的反作用力为 {F}_{B1x}^{\prime }\text{、}{F}_{B1y}^{\prime } ,还受到钢丝绳对销 B 的拉力 {F}_{B}^{\prime } 的作用。销 B 的受力图如图 18g 所示。
(7)画整个系统的受力图,取整体为研究对象。把整个系统刚化为刚体,其上铰链 B\text{、}C\text{、}D 处与钢丝绳各处的作用力均为内力,故可不画。系统的外力除主动力 \mathbf{P} 外,还有约束力 {\mathbf{F}}_{A} 与 {\mathbf{F}}_{Ex} 、 {\mathbf{F}}_{Ey} 作用,整体受力图如图 18h 所示。
(8)画销 B 与滑轮 \mathrm{I} 一起的受力图,取销 B 与滑轮 \mathrm{I} 一起作为研究对象。销 B 与滑轮 \mathrm{I} 之间的力为内力,不用画出。其上除受三绳拉力 {\mathbf{F}}_{B}^{\prime }\text{、}{\mathbf{F}}_{1}^{\prime } 和 {\mathbf{F}}_{K}^{\prime } 外,还受到二力杆 {BD} 与杆 {AB} 在 B 处对它的力 {F}_{BD}^{\prime } 和 {F}_{Bx}^{\prime }\text{、}{F}_{By}^{\prime } 的作用。其受力图如图 18i 所示。
(9)画杆 {AB} ,滑轮 I 、II ,钢丝绳和重物为一个系统时的受力图;取杆 {AB} ,滑轮 I 、III,钢丝绳和重物为一体作为研究对象。把此系统刚化为一个刚体,这样,销 B 与杆 {AB} ,滑轮 \mathrm{I} 、 \mathrm{{II}} ,钢丝绳之间的力,都是内力,可不画。系统上的外力有主动力 \mathbf{P} ,约束力 {\mathbf{F}}_{A} 、 {\mathbf{F}}_{BD}^{\prime } 与 {\mathbf{F}}_{Cx} 、 {\mathbf{F}}_{Cy} 外,还有 K 处的钢丝绳拉力 {F}_{K}^{\prime } 。其受力图如图 18j 所示。
此例中铰链 B 连接有杆 {DB} 、杆 {AB} 、滑轮 \mathrm{I} 和钢丝绳四个构件,因此,在将各构件在 B 处分离时必须明确销的位置。
正确地画出物体的受力图,是分析、解决力学问题的基础。画受力图时必须注意以下几点:
-
(1)必须明确研究对象,画出其分 (隔) 离体图。根据求解需要,可以取单个物体为研究对象,也可以取由几个物体组成的系统 (有的称之为子系统) 为研究对象。一般情况下,不要在整个系统的简图上画某一物体或某子系统的受力图。
-
(2)正确确定研究对象受力的数目。主动力、约束力均是物体受力,均应画在受力图上。所取研究对象 (分离体) 和其他物体接触处,一般均存在约束力,要根据约束特性来确定,严格按约束性质来画,不能主观臆测。
-
(3)注意作用力和反作用力的画法,作用力的方向一旦假定,图上的反作用力一定与之反向。
-
(4)注意二力构件(杆)的判断,是二力构件(杆)最好按二力构件(杆)画受力图。
-
(5)物体与物体未拆开(分离)处相互作用的力称为内力,内力一律不画在受力图上。
-
(6)受力分析过程不要用文字写出,按要求画出受力图即可。
6 力学模型与力学简图
把力学模型用简单的图形表示出来,称为力学简图。对任何实际的力学问题进行分析、计算时,都要将其抽象为力学模型。
在建立力学模型时,要抓住关键、本质的因素,忽略次要的因素。例如,图 5 所示的圆柱,它在受力时肯定会变形,但我们忽略它的变形,把它看成是刚体。它的几何形状不可能是严格数学意义上的圆形,但我们把它看成是圆形。它是三维的物体,我们把它简化为平面问题。圆柱的重心不会恰好在图中的圆心,但我们将圆柱材料看成是均匀的,几何形状是圆形,因此其重心在圆心。 A\text{、}C 处的约束也不会绝对光滑,但我们忽略摩擦; A\text{、}C 处实际上是面接触,但我们简化为平面问题中的点接触,如此才能用集中力 {\mathbf{F}}_{\mathrm{N}A}\text{、}{\mathbf{F}}_{\mathrm{N}C} 表示约束力; 等等。可见,将一个实际问题简化为力学模型,要在多方面进行抽象化处理。
6.1 简支梁的力学模型
图 19 所示是一种常见的力学模型,一般称为简支梁。那么,什么样的实际力学问题可以用此力学模型来表示?
它可以是由一实际单跨水泥桥梁简化而来,如图 20 所示。水泥桥梁直接放在桥墩上。固定铰链支座并不是如图 10 所示由销与穿孔的底座构成。滚动支座也不是如图 11a 所示在底座和基础之间垫上滚子构成。 但因为桥梁直接放在桥墩上,接触处的摩擦可以限制桥梁产生很大的水平位移,所以就相当于有一固定铰链支座。又因为物体的弹性,桥梁可以自由热胀冷缩,所以就相当于垫有滚子。因此,实际的单跨水泥桥梁可以简化为图 19 所示的力学模型。

图 19

图 20
类似的实际问题还有两端直接放在河岸上的独木桥;两端直接放在砖墙上的木梁。由于同样的原因,均可用图 19 所示的力学模型表示。
6.2 平面桁架的力学模型
工程中,房屋建筑、桥梁、起重机、油田井架、电视塔等结构物常用桁架结构。
桁架是一种由直杆在两端用铰链连接且几何形状不变的结构,桁架中各杆件的连接点被称为节点。若桁架中各杆件轴线均在同一平面内 (几何平面),且载荷也位于此平面内的桁架被称为平面桁架。平面桁架就是一种简化后的力学模型。 实际中的许多结构均可简化为平面桁架。
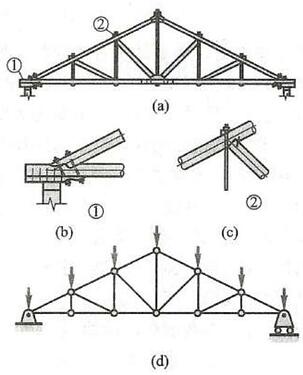
图 21a 所示为一木屋架示意图,经简化后,其力学模型如图 21d 所示,为一平面桁架。此屋架两端直接放在墙上,两端并不是由如图 10 所示和图 11 所示的固定铰链支座和滚动支座构成,但如上所述,两端可用如图所示固定铰链支座与滚动支座表示。
图 21
此屋架中的五根竖直杆可为铁条或木头,其他主要部分为木头。局部①处为螺栓连接,如图 21b 所示,局部②处用螺帽加箍钉连接,如图 21c所示。其各连接处并不是图 10 所示的圆柱形铰链连接方式,但可以简化为圆柱形铰链连接。原因是这种约束主要限制杆件的线位移,而不是角位移。如同一直细铁条,细铁条短,其轴线为直线; 细铁条长,则自然会弯曲。因为杆比较细长,杆件绕连接处 (点) 有些微转动,这种连接 (约束) 限制不了杆件的转动,所以可简化为铰链连接。
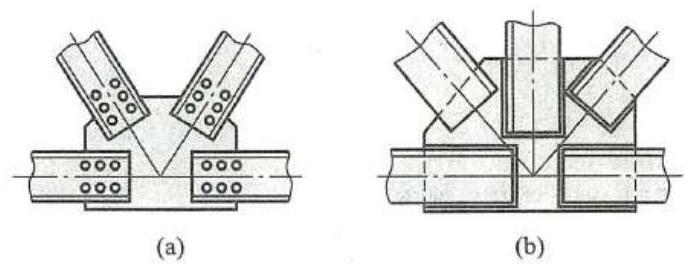
实际上,这些连接处还可以是铆接、焊接等,如图 22 所示。如果全是木质结构,这些连接处还可以是榫卯连接。
图 22
因此,铰链连接可以是图 10 所示的连接方式,但在很多实际结构中,螺栓连接、铆接、焊接、榫卯连接等均可看作铰链连接。
实际中的桁架,各杆件均有自重,其载荷也不作用在节点上,这样计算起来非常复杂。为了满足工程要求且简化计算,通常用力系等效替换的方法,把所有载荷均等效到节点上,如图 21d 所示。
图 21d 所示就是图 21a 所示实际屋架简化的力学模型,计算图 21a 所示实际屋架的受力,就是通过计算图 21d 所示的力学模型来完成的。
6.3 人体中的力学模型
在力学研究中,一般把人体骨骼抽象为刚体,关节处抽象为铰链,肌肉可看作柔索,即可建立人体的力学模型。
如图 23a 所示,人的胳膊呈 90° 手握一重物,其重心位于点 {C}_{1} ,小臂重心位于点 {C}_{2} ,重量均为已知。小臂骨可抽象为一直杆,骨关节 B 处可抽象为一铰链,肌肉 {CD} 可视为一柔索(或拉杆),则抽象出的力学模型如图 23b 所示。给出载荷和尺寸就可计算肌肉 {CD} 与骨关节 B 处的受力。
图 23