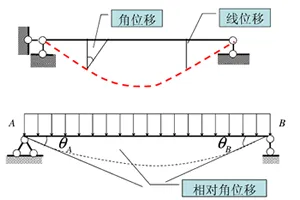
结构实位移及虚位移
变形: 结构在荷载作用下,会产生应力和应变,以致结构的原有形状会发生变化,这种变化称为变形。
位移: 结构变形时,结构上某个点发生的移动或某个截面发生的转动,称为结构的位移。
除了载荷作用将引起位移外,温度改变、支座移动与制造误差等因素,虽然不一定使结构都产生应力和应变,但都将使结构产生位移。
位移的分类: 线位移和角位移。
结构位移计算的目的
-
验算结构的刚度;
-
为超静定结构的内力计算打下基础;
-
结构制作、施工的需要。
结构计算位移的假定
-
材料服从胡克定律。
-
结构的变形是微小的。
-
结构各处的约束都是理想约束。
实位移: 由于运动而实际发生的位移,对应的时间间隔dt,同时满足运动微分方程,可表示为:d\overrightarrow{r} =\overrightarrow{v} dt
虚位移 :t 时刻,质点在约束允许情况下可能发生的无限小位置变更。
虚位移是可能位移,纯几何概念(非运动学概念):
(1) 特点(本质):想象中可能发生的位移,它只取决于质点在 t 时刻的位置和约束方程,并不对应一段时间间隔 \delta t ,它是一个抽象的等时变分概念。
(2) 直观意义(求法):
对于非稳定约束,在 t 时刻将约束“冻结”,然后考察在约束允许情况下的可能位移,即视约束方程中的 t 不变( \delta t *=0),对约束方程进行等时变分运算(同微分运算,注意 \delta t =0)即可得虚位移;
对于稳定约束,由于约束方程中不显含t,“冻结”已无实际意义,等时变分运算与微分运算完全相同。比如:质点被限制在以等速u匀速上升的水平面内运动,约束方程为:z-ut=0,\delta z=0,dz=udt。
(3) 实位移是唯一的,虚位移可若干个;对稳定约束,实位移为若干个虚位移中的某一个;对非稳定约束,实位移与虚位移不一致。
实功、虚功及理想约束
实功: 作用在质点上的力(含约束力)在实位移中所作的功,dw。
虚功: 作用在质点上的力(含约束力)在任意虚位移中所作的功,δw。如果使力做功的位移不是由于该力本身所引起,即做功的力与相应于力的位移彼此独立,二者无因果关系,这时力所做的功称为虚功。
理想约束: 体系所受诸约束反力在任意虚位移中所作元功之和等于零。
虚功与实功的差别:
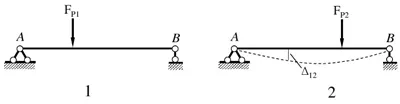
W_{11} =\frac{1}{2} F_{P1} \times \Delta _{11}
W_{22} =\frac{1}{2} F_{P2} \times \Delta _{22}
W_{12} =F_{P1} \times \Delta _{12}
所谓“虚“就是表示位移与做功的力无关。\Delta _{ij} 的第一个脚标表示位移发生的位置和方向,即此位移是 F_{Pi} 作用点沿 F_{Pi} 方向的位移;第二个脚标表示产生位移的原因,即此位移是由 F_{Pi} 引起的。
状态1的力在状态2的位移上所做的虚功:
W_{12} =F_{P1} \times \Delta _{12}
状态1上的力也可以不是一个力,而是一组力;状态2上的虚位移也可以不是一个力或一组力引起的,而是其他因素,比如温度改变、支座移动等引起的。虚位移可以理解为结构可能发生的连续的、微小的、约束所允许的位移。
虚功原理
1. 刚体体系的虚功原理
具有理想约束的刚体体系在任意平衡力系作用下,体系上所有主动力在任一与约束条件相符合的无限小刚体位移所做的虚功总和恒等于零。刚体体系的虚功方程:
W=0
(1) 虚设位移状态,求未知力
拟求C点的竖直向位移:
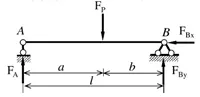
W=F_{A} \times \Delta _{A} +F_{P} \times \Delta _{P} =0
F_{A} =-F_{P} \times \frac{\Delta _{P} }{\Delta _{A} }
\frac{\Delta _{P} }{\Delta _{A} } =-\frac{b}{l}
F_A=\frac{b}{l} \times F_{P}
虚位移原理:
F_{A} =-F_{P} \times \delta _{P}
应用虚位移原理求解静定结构的某一约束力时,一般应遵循如下步骤:
(1) 解除欲求约束反力的约束,用相应的约束反力来代替。
(2) 把机构可能发生的刚体位移当作虚位移,写出虚功方程。
(3) 求出虚位移之间的几何关系,利用虚功方程即可求解约束反力
(2) 虚设力状态,求未知位移
拟求C点的竖直向位移:
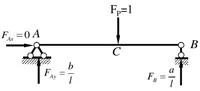

虚力原理:
F_{P} \times \Delta _{C} +F_{B} \times c=0
\Delta _{C} =-\frac{F_{B} }{F_{P} } \times c=-\frac{ac}{l}
当支座有给定的位移时,静定结构的位移可用虚力原理求解。设支座n有给定位移cn(n=1,2,3,…),计算步骤如下:
(1) 沿拟求位移Δ方向虚设相应的单位荷载,并求出单位荷载作用下的支座反力;
(2) 令虚设位移在实际位移上作虚功,写出虚功方程:
1\times \Delta +\sum \overline{F} _{Rn} c_{n} =0
(3) 由虚功方程,解出拟求位移为:
\Delta =-\sum \overline{F} _{Rn} c_{n}
2. 变形体体系虚功原理
变形体体系的虚功原理可表述为:处于平衡状态的变形体体系,当发生符合约束条件的微小连续变形,则外力在位移上所做的外虚功 W_e 恒等于各个微段的应力合力在变形上所做的内虚功 W_i,即 W_e=W_i 。
变形体体系的虚功方程:
W_{e} =W_{i} =\sum \int \left ( F_{N} \varepsilon +F_{\varrho} \gamma +M\kappa \right ) ds
其中:\varepsilon 为相对轴向应变,\gamma 为相对切应变,\kappa 为相对轴线曲率。
力状态的外力在位移状态的位移上所做的外力虚功,等于力状态的内力在位移状态的变形上所做的内力虚功。对于弹性、非弹性、线性、非线性的变形体体系均适用。
结构位移计算
结构位移计算的一般步骤:
已知杆件结构各微段的应变 \varepsilon 、 \gamma 、\kappa 和支座位移 c_{n} ,拟求结构某点沿某方向的位移 Δ_k ,计算步骤如下:
(1) 沿拟求位移 Δ_k 方向虚设相应的单位载荷。
(2) 在单位载荷作用下,根据平衡条件,计算结构的支反力和内力。
(3) 利用结构位移计算的一般公式计算位移Δk。
如果求得的位移 Δ_k 为正值,说明位移的实际方向和虚设的单位载荷的方向一致;否则方向相反。