作为一种数值计算方法,无网格法和有限元一样,都是通过变分原理推导控制方程,但也存在很多不同之处。
1 形函数不同
无网格法将研究对象离散为节点,节点之间无需网格联系,节点的函数值是该节点影响域内节点的函数值通过最小二乘拟合或积分变换得到的,即形函数不是插值函数。而有限元法将研究对象离散为单元,以单元为研究对象,单元内任意点的函数值通过节点值插值得到,形函数为插值函数。
无网格法:
节点 x 处的近似函数值: u^h(x) = \sum_{i=1}^n \Phi_i(x) u_i 其中:
- \Phi_i(x) 为形函数,基于节点影响域内的最小二乘拟合;
- u_i 为节点 i 的函数值;
- n 为影响域内节点数。
形函数 \Phi_i(x) 通常通过权函数和基函数构造: \Phi_i(x) = \mathbf{p}^T(x) \mathbf{A}^{-1}(x) \mathbf{B}_i(x) 其中:
- \mathbf{p}(x) 为基函数向量(如 [1, x, y]^T );
- \mathbf{A}(x) = \sum_i w(x - x_i) \mathbf{p}(x_i) \mathbf{p}^T(x_i);
- \mathbf{B}_i(x) = w(x - x_i) \mathbf{p}(x_i);
- w(x - x_i) 为权函数(如高斯权函数)。
有限元法:
单元内任意点函数值: u^h(x) = \sum_{i=1}^n N_i(x) u_i 其中:
- N_i(x) 为插值形函数(如线性三角形单元的形函数);
- u_i 为节点 i 的函数值;
- n 为单元节点数。
例如,二维线性三角形单元的形函数: N_i(x, y) = a_i + b_i x + c_i y 其中,a_i, b_i, c_i 通过节点坐标和插值条件解出。
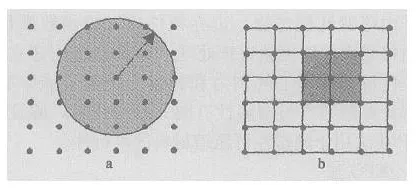
a) 无网格法;b) 有限元法
图1 无网格法和有限元法离散方式的区别
2 整体刚度矩阵的组成
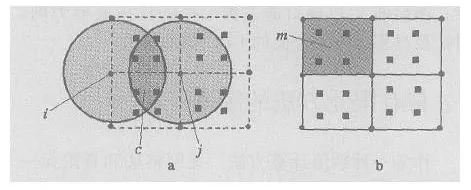
在系统刚度矩阵的组成上,有限元法是对单元内的高斯点积分,其刚度矩阵是通过单元内的高斯点组合起来的;而无网格法是对 I 节点影响域和 J 节点影响域交集中的高斯点积分,刚度矩阵是交集中的高斯点的组合。
无网格法:
刚度矩阵: \mathbf{K}*{IJ} = \int*{\Omega_{IJ}} \mathbf{B}_I^T \mathbf{D} \mathbf{B}_J , d\Omega 其中:
- \Omega_{IJ} 为节点 I 和 J 影响域的交集;
- \mathbf{B}_I = \nabla \Phi_I(x) 为形函数梯度;
- \mathbf{D} 为材料刚度矩阵。
有限元法:
刚度矩阵: \mathbf{K}*{e} = \int*{\Omega_e} \mathbf{B}^T \mathbf{D} \mathbf{B} , d\Omega 其中:
- \Omega_e 为单元区域;
- \mathbf{B} = \nabla \mathbf{N} 为形函数梯度矩阵;
- \mathbf{D} 为材料刚度矩阵。
a) 无网格法;b) 有限元法
图2 无网格法和有限元法整体刚度矩阵的组成
3 本质边界条件的处理
如前所述,无网格法的形函数不是插值函数,即函数在某点的近似值不等于函数在该点的值,所以本质边界条件不能满足,这也是无网格法最大的困难,解决的方法有:罚函数法、拉氏乘子法、修正的变分原理法、与有限元耦合法等。其中,罚函数法虽然其精度受罚函数的影响较大,但由于比较简单而得到广泛应用。
4 积分方案不同
有限元一般采用高斯积分,即在单元内部建立高斯积分点。
而无网格法采用的积分方案有:
- 节点积分,即利用梯形积分法则,这种方法比较简单,是真正的无网格法,但计算稳定性较差;
- 利用背景网格或有限元背景网格建立高斯积分过程,这里的网格仅用于积分计算,并不影响无网格法的实质。