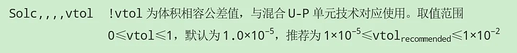在有限元分析中,计算结果与理论预期不符是常见问题,其中剪切自锁(Shear Locking)和体积自锁(Volumetric Locking)是两类典型的数值误差。这两种“锁死”现象使单元表现出过高的刚度,导致变形结果显著低于实际值,并可能影响非线性分析的收敛性。本文分析两者的力学机理、典型特征及工程实践中的解决方案。
剪切自锁:弯曲变形“冻结”之手
定义与机理
剪切自锁(Shear Locking)是有限元分析中的常见数值问题,指在纯弯曲等理论上无剪切变形的场景中,由于单元插值函数的局限性,产生了寄生剪切应变,导致位移结果偏小。
其本质是低阶单元的位移场插值函数无法准确描述弯曲变形,引入了非物理的“伪剪切应变”。这些寄生应变消耗了部分变形能,导致单元表现出过高的刚度,计算结果偏离实际。
力学原理
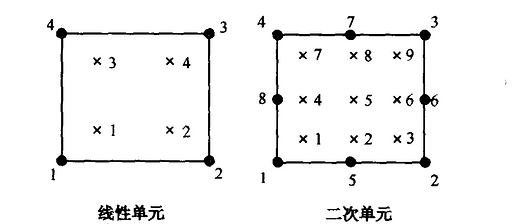
根据材料力学中的平截面假定,纯弯曲时,截面保持平面且垂直于中性轴,理论上无剪切应力。然而,在有限元分析中,低阶线性单元(如四节点四边形Q4)的形函数仅支持线性位移插值,无法准确表达弯曲引起的二次位移场,导致寄生剪切应变,如图1所示。
以受纯弯曲的单元为例,单元上表面拉伸、下表面压缩,与理论一致。但由于线性形函数的限制,单元内部产生非物理的剪切应变(如图1b所示,单元变形为梯形,虚线夹角偏离90°),导致伪剪切应力。这种寄生应变减少了实际弯曲变形,使单元表现出过高刚度,位移结果显著低于理论值。
(a) 单元正常弯曲变形
(b) 单元剪切自锁变形
图1 单元正常弯曲与剪切自锁
当应用完全积分线性单元来模拟受纯弯曲的小块材料时,单元上表面拉伸,下表面压缩,这些都与纯受弯的小块材料一致,但是在每个积分点处,中间直线被迫“倾斜”,表现为图1所示的竖直虚线和水平虚线之间的夹角不再为90°,这说明了这点的剪应力不为零,即在积分点处产生了伴生剪切,这与纯受弯的情况不符。
这种伪剪切变形消耗了变形能,而不产生所希望的弯曲变形,使得实际弯曲变形减小,即表现为单元“过硬”,计算得到的挠度可能比理论值低30%以上。
影响因素
剪切自锁的严重程度与以下因素密切相关:
- 单元阶次:低阶线性单元(如Q4)比高阶二次单元(如Q8)更容易发生锁死;
- 受力状态:以弯曲为主的工况(如梁受纯弯矩);
- 网格形态:单元长宽比越大,锁死现象越显著。
二次单元因边界支持二次形函数,能较好地描述弯曲变形,通常无严重的剪切自锁。然而,在复杂应力状态下(如单元扭曲或存在显著的应力梯度),二次单元也可能出现一定程度的剪切自锁。
图2 完全积分的线性单元与二次单元
但是如果二次单元发生扭曲或它的弯曲应力有梯度(复杂受力状态),那么也将有可能出现某种程度的剪切自锁,这两种情况在实际问题中是可能发生的。
因此,对于完全积分的线性单元,我们只有当确信载荷只会在模型中产生很小的弯曲时,才可以采用完全积分的线性单元。如果对载荷产生的变形类型有所怀疑,可应采用不同类型的单元分析对比。
对于完全积分的二次单元,在复杂应力下也有可能发生自锁,因此如果在模型中应用这类单元,也应仔细检查计算结果。
① 采用缩减积分单元
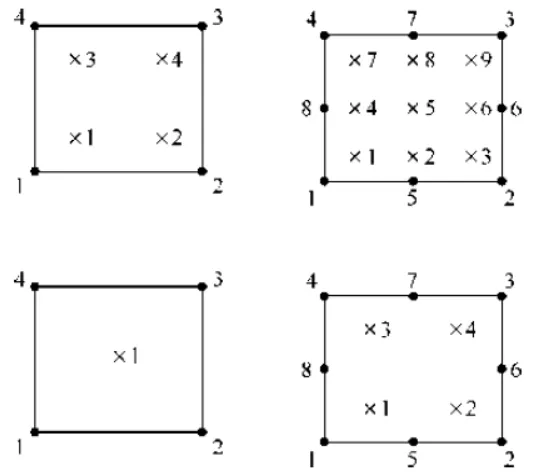
缩减积分的概念如图3所示,上图为完全积分,下图为缩减积分(注意在ANSYS软件中 ,Full Integration 实际是选择缩减积分,即将求解应变的矩阵分为体积项和偏差项,对体积项采用缩减积分,对偏差项采用完全积分)。此处所讲的缩减积分(Reduced Integration)是对体积项和偏差项均采用缩减积分。但该方法会出现沙漏(变形的零能模式)。
图3 完全积分单元与缩减积分单元
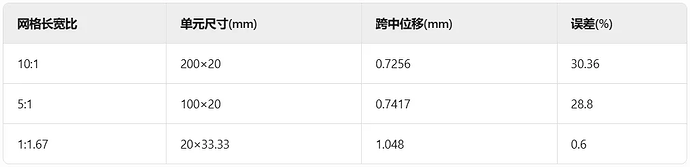
值得注意的是,剪切自锁现象还受到单元长宽比的较大影响。如下表所示,有分析表明:当简支梁网格长宽比达到10:1(200mm×20mm单元)时,即使用缩减积分,跨中位移误差仍高达30%;而当采用近正方形单元(20mm×33.33mm)时,结果与理论解(1.042mm)基本吻合。
② 采用增强应变单元(非协调单元)
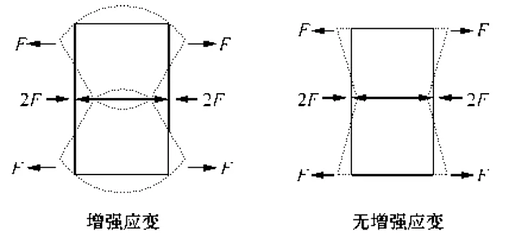
增强应变单元通过引入额外的应变自由度提高形函数灵活性,适用于低阶四边形或六面体单元(如图4所示)。此方法有效缓解剪切自锁,且不引入沙漏模式。单元质量越高,计算精度越高。计算原理如图4所示,在单元中附加了自由度相当于提高了形函数的阶数;同时允许网格中产生缝隙和重叠,故也称为非协调模式。
图4 增强应变单元
③ 采用高阶单元
如前所述,剪切自锁主要是因为线性单元的边不能弯曲,因此采用二次或更高阶单元(如PLANE183),可大为缓解剪切自锁现象,但这会造成计算成本增加。
④ 网格优化
-
控制单元长宽比(建议<4,复杂问题<3)。
-
在弯曲方向布置足够单元层数(至少3层,确保捕捉弯曲应变梯度)。
-
优先在高应力梯度区域细化网格。
体积自锁:不可压缩材料的“刚性枷锁”
与剪切自锁不同,体积自锁主要发生在处理近似不可压缩材料(如橡胶、生物软组织)的仿真中,当泊松比υ接近0.5时,完全积分单元会出现体积应变被过度约束的现象。从本构关系看,体积模量K的计算公式为:
![]()
体积自锁的产生需要两个条件:
① 使用完全积分单元;
② 材料泊松比接近0.5。
值得注意的是,平面应力问题不会出现体积自锁,因为平面外应变可补偿体积变化。对于非平面应力问题,如何缓解体积自锁呢?通常可采取如下措施:
①采用混合U-P单元(杂交单元)
混合U-P(位移-压力)公式是解决体积自锁最有效的方法。其核心思想是将静水压应力(图5)作为独立自由度引入单元,与位移场分开求解。
静水压力(hydrostatic pressure)是应力张量中各向同性的部分,表示为所有主应力的平均值。其数学表达式为:
p = -\frac{1}{3}(\sigma_1 + \sigma_2 + \sigma_3)
其中,\sigma_1 、\sigma_2 、\sigma_3 是主应力(principal stresses)。负号表示在固体力学中,压应力通常定义为负值。静水压力是一种等向性应力状态,作用于材料的所有方向,引起体积变化而非形状变化。
图5 静水压力下的单元
在ANSYS中,采用U-P杂交单元可通过插入命令流实现。设置KEYOPT(6)=1启用该技术,同时建议配合体积相容公差(VTOL,默认1e-5)调整,如下:
例如对SOLID185单元,可插入command添加如下命令流:① 在橡胶材料下启用U-P杂交单元:
KEYOPT,MATID,6,1
② 在求解栏中插入一条 Command:
/SOLU
SOLC,1E-3
② 此外缓解体积自锁现象的其他措施还包括:
B-Bar方法:对体积应变项单独降阶积分;
增强应变单元技术:适合六面体/四边形单元;
材料调整:υ设为0.495~0.499平衡精度与收敛;
缩减积分:但需警惕沙漏效应。
精准仿真的“解锁”之道
在实际工程中,应对剪切自锁和体积自锁的“抗锁死”技术需权衡计算精度、稳定性和效率。
需要特别注意的是,应对剪切自锁或体积自锁的这些技术往往会相互影响甚至冲突。例如同时采用缩减积分和增强应变可能导致过度软化。在应对这些问题时建议:
① 先尝试网格细化,厚度方向应至少3层单元;
② 对于橡胶密封件,首选混合U-P单元技术;
③ 关注沙漏能比率,尽量控制在<5%,不应超过10%。
剪切自锁和体积自锁作为有限元分析中的典型数值问题,其本质都是单元形函数与实际变形模式不匹配导致的过度约束现象。理解其背后的力学原理(如平截面假定、体积模量发散)和数值机理(积分方案、形函数阶次),才能合理选择单元技术。现代商业软件(如ANSYS、ABAQUS)虽然提供了多种高级单元选项,但作为工程师仍需掌握“问题诊断—方法匹配—结果验证”的完整闭环,特别是在处理非线性材料或复杂接触时,建议通过小规模试算验证单元技术的适用性。