在计算流体力学中(CFD)中,高精度的仿真结果始于高质量的网格。网格的三个方面决定了求解器的计算精度:网格质量、网格分辨率和网格对齐。网格质量是指单元的形状是否合理,例如是否存在过度扭曲、拉伸,这些因素会影响数值计算的稳定性和收敛性。高质量的网格对于仿真来说非常重要。
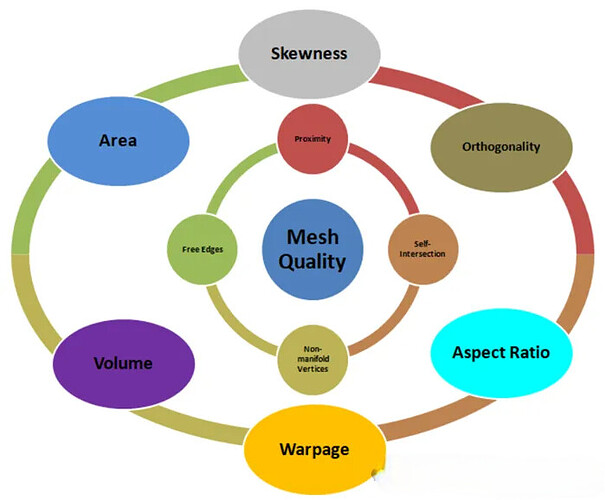
网格的评价指标
网格分辨率也就是网格大小,决定了计算域内流场特征的捕捉能力,较高的分辨率有助于更准确地解析边界层、涡结构和湍流特性。
不同的网格分辨率
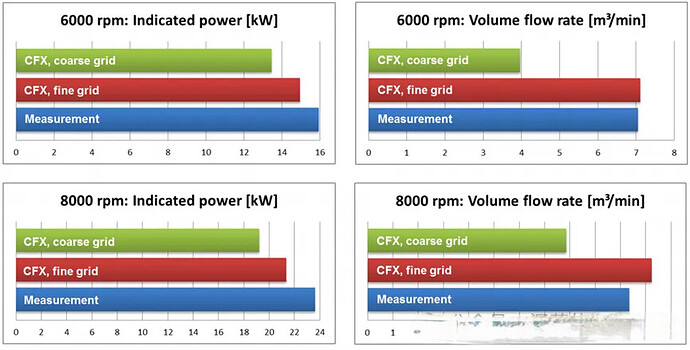
高分辨率的网格更接近实测结果
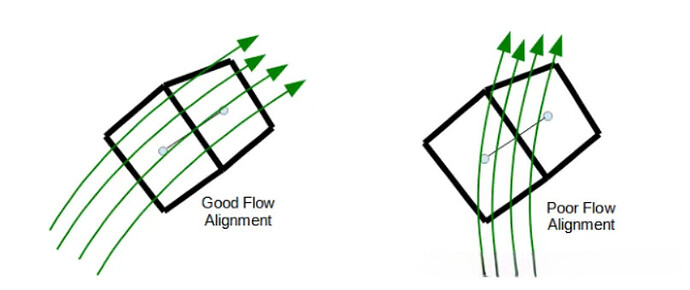
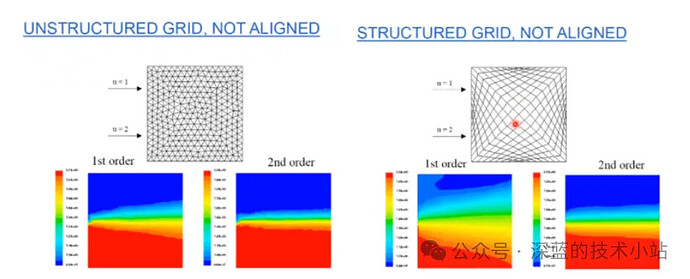
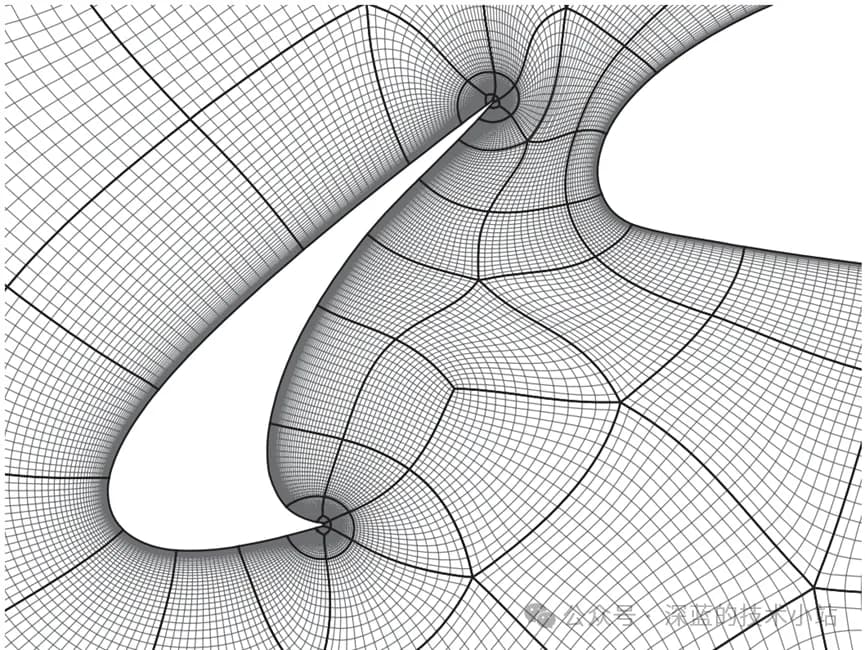
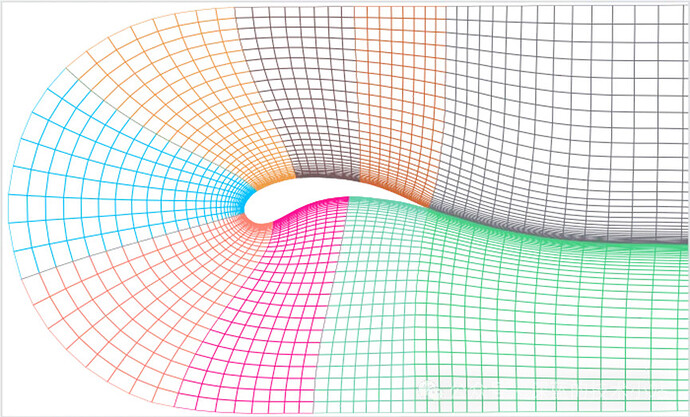
大多数情况下,我们对网格质量和网格分辨率非常关心,但是却忽略了网格线和流动方向对齐对于流动结果的影响。网格对齐即在CFD网格生成过程中,遵循流动方向布置网格,即使在非结构化网格中,也尽可能使单元的主方向与流动方向对齐。网格对齐对于降低数值误差、提高模拟精度同样至关重要。合理的网格对齐可以减少数值扩散,使得流动特征(如剪切层、涡旋结构、冲击波等)能够更加清晰准确地被捕捉。如下图,左边的网格与流动方向对齐的很好,右边的网格偏离了流动方向。
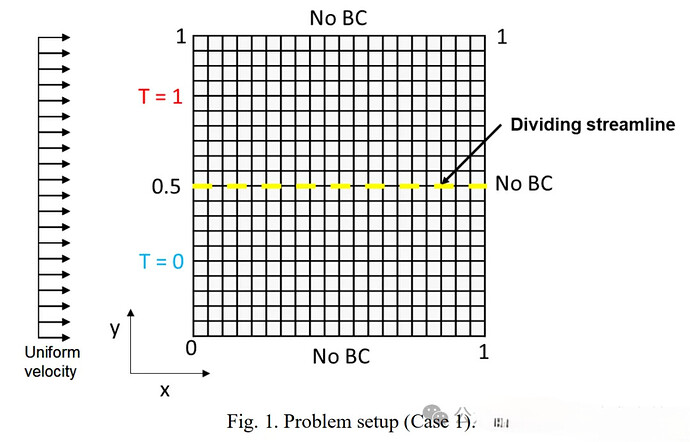
接下通过一个案例说明,网格线与流动方向对齐对于结果的重要性。假定一个简单的稳态不可压缩、无粘空气流动对流问题,其基本能量方程为:
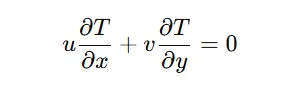
这个方程表示温度 T(x,y) 随着速度场 (u,v) 进行对流传输,在无扩散的情况下,温度场会沿着流动方向传输,而不会发生任何混合。若初始温度场存在不连续性,理论上该不连续性会一直沿流动方向保持,不会产生混合层。
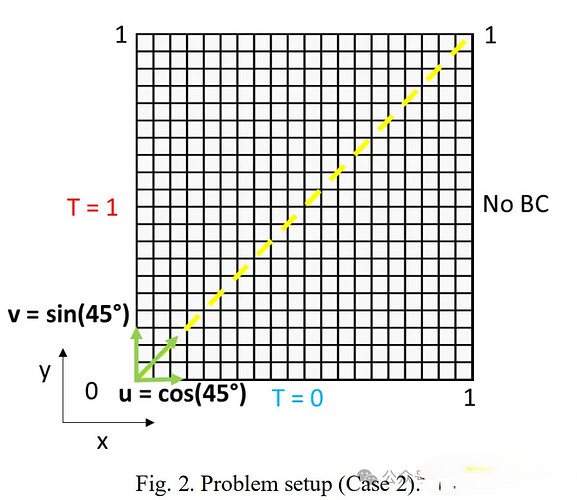
设定两种流向情况,在case1中流向与网格线方向一致,即夹角为0°,流向与网格线方向一致。在case2中,流向与网格线夹角为45°,流向与网格线方向不一致。观察结果中是否有扩散的情况发生。
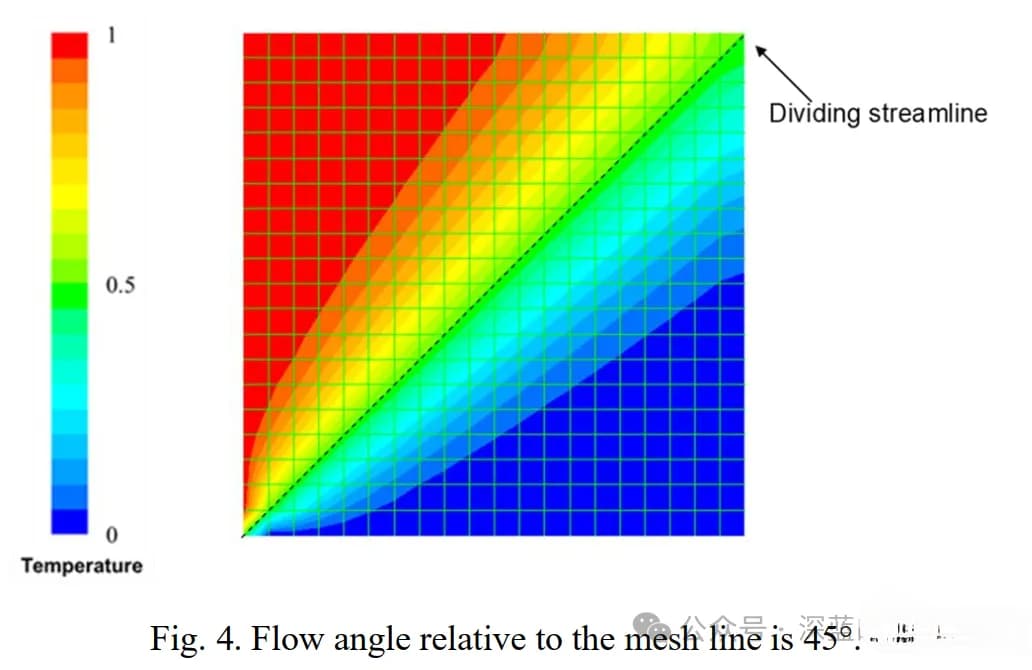
从结果中可以看到,当流向与网格线对齐的情况下,没有观察到混合层,温度场沿流线方向保持清晰的分界。这表明此时数值扩散的影响最小。在流向与网格线成 45° 角的情况下,出现了显著的数值扩散现象。模拟结果显示温度分界线附近出现混合层。
从这个案例中我们可以看到流动方向和网格线一致的重要性。除此之外,使用高阶的数值方法能够减少这种数值扩散。
在 CFD 模拟中,网格的选择和数值方法的精度对计算结果的准确性有着至关重要的影响。特别是在复杂流场中,合理的网格生成策略和先进的数值方法相结合,将极大提升流体模拟的可靠性和计算效率。
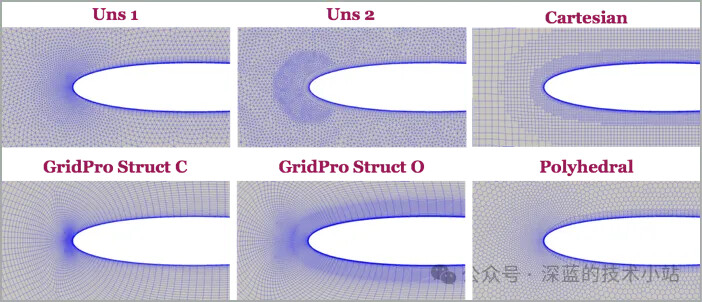
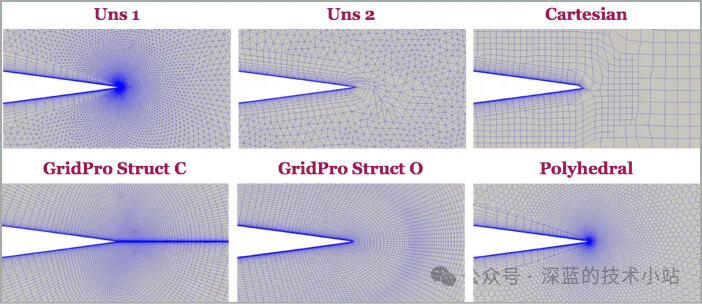
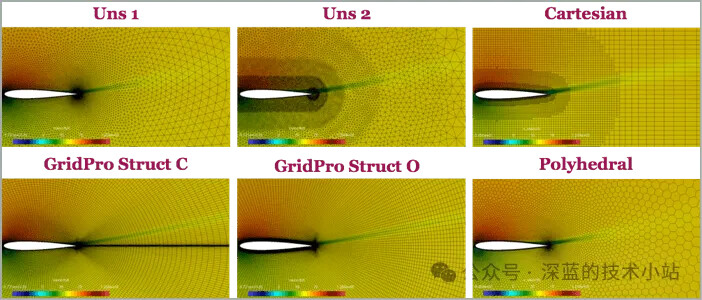
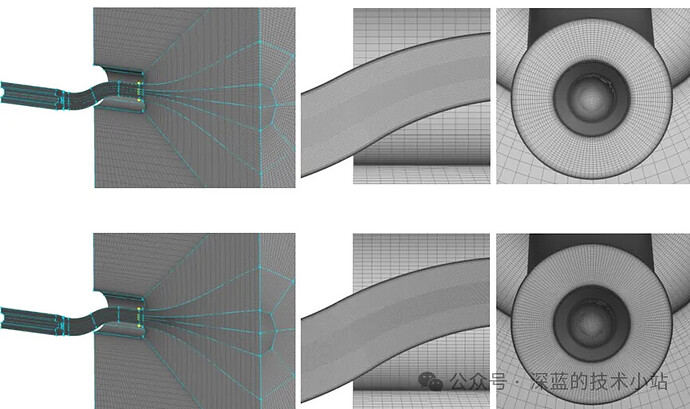
使用NACA-0012 翼型的标准测试案例,测试不同网格的仿真结果与实验结果的误差。首先需要说明的一点是,虽然外部网格是不同类型的网格,但是机翼边缘的网格使用了结构化网格进行细化。
机翼整体网格
机翼前部网格
机翼后部网格
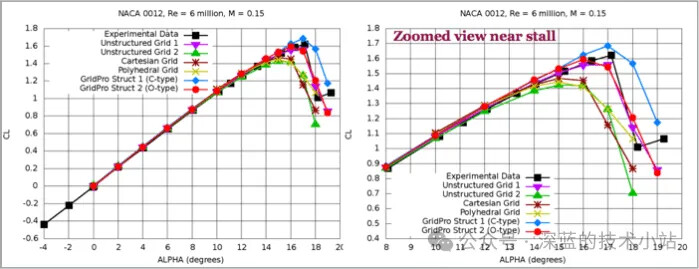
每一个测试案例的网格数量和节点数量几乎都相同,使用Fluent求解器进行求解,计算攻角(Alpha)从 0° 到 19° 变化,以研究不同攻角下的空气动力特性。
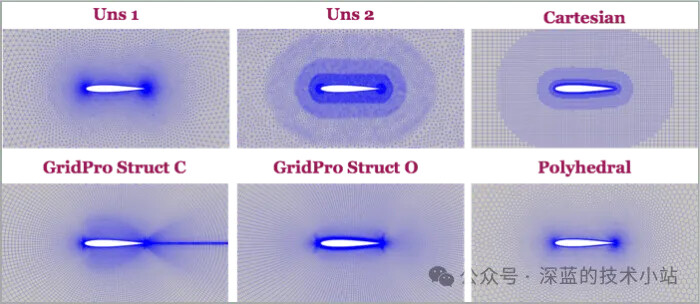
从CL-α 曲线和CD-α 曲线曲线中可以得出一些简单的结论,相比于结构化网格和非结构化网格,笛卡尔网格的精度低;而在结构化网格和非结构化网格的对比中,结构化网格的精度更高。这也与我们的经验和常识相符,通常的流体网格以结构化网格为主,网格线的方向会与流向方向对齐以减少数值扩散。
在一些几何模型特别复杂,流动情况特别复杂的情况下,划分结构化网格非常困难,为了仿真时间和精度的权衡,通常会使用非结构化网格来对流体域进行网格划分。