在有限元分析（FEA）中，利用对称性是一种减少计算规模的有效方法。本文将详细介绍如何应用对称性，以及在反对称、对称和轴对称情况下的应用。
何时可以应用对称性？
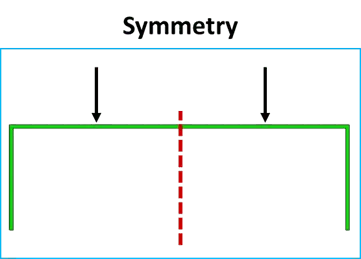
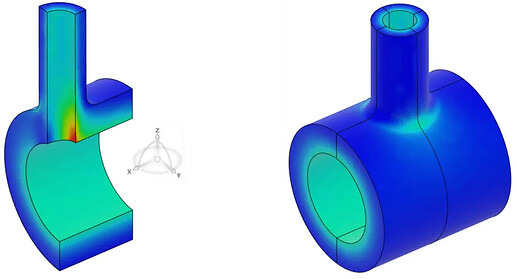
在FEA中提到的“对称”通常指的是镜面对称。如果模型的几何形状、边界条件和载荷关于镜像平面对称，则可以沿该镜像平面应用对称边界条件。这样做的好处是显著的；对称性实际上可以将模型的尺寸减半。例如，下图展示的相交管道模型关于XZ和YZ平面双对称——通过使用对称性，我们能够将模型的尺寸缩小75%！
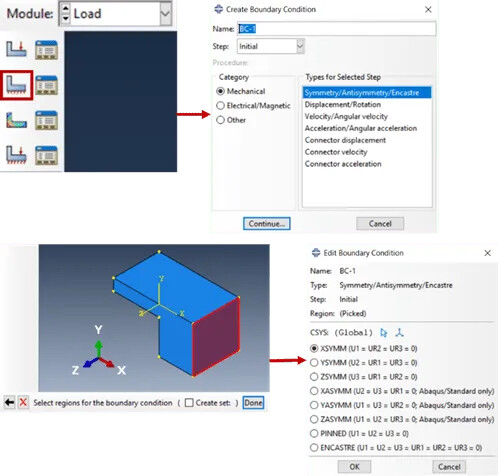
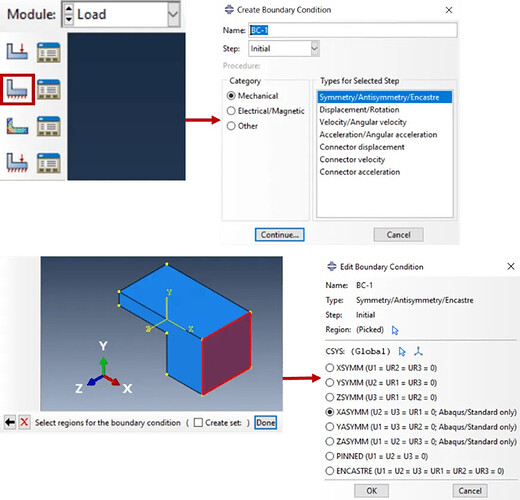
在Abaqus CAE中应用对称边界条件
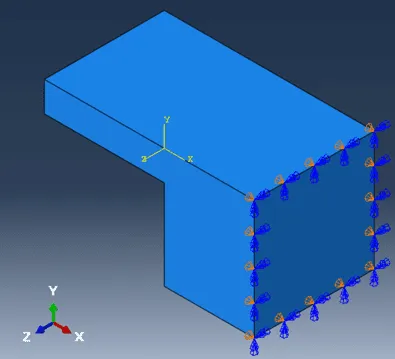
要沿平面应用对称边界条件，必须约束法线方向上的位移和沿平面轴的旋转。例如，围绕YZ平面（或X轴平面）的对称性限制了沿X的平移以及围绕Y和Z的旋转。
这可以通过手动约束所需的自由度来完成；或者在Abaqus CAE中可以直接应用对称边界条件。
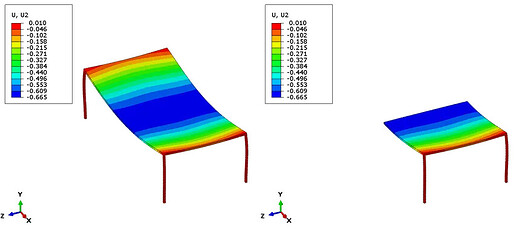
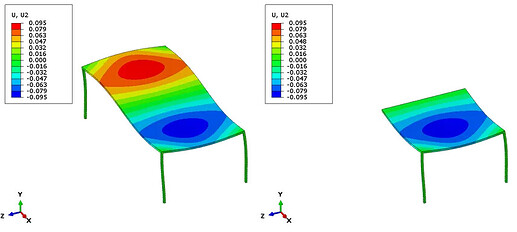
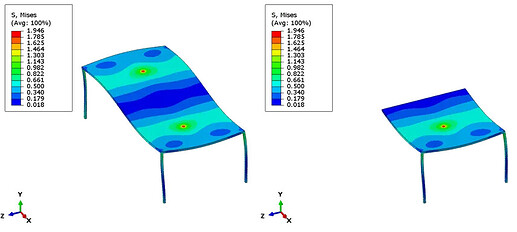
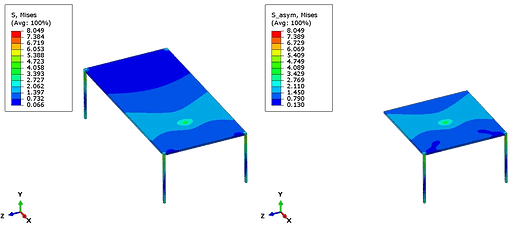
为了证明这是有效的，我们将使用一个简单桌子的模型来验证。我们在一个模型中运行了整个桌子模型，并在两侧施加相同的向下负载，第二个模型则运行了1/2模型，并使用对称边界条件，结果是相同的：
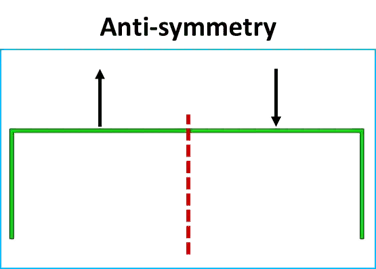
反对称性
如果几何形状关于镜面对称，但载荷相等且方向相反，则可以沿镜面应用反对称边界。要沿平面应用反对称边界条件，必须约束法向方向的旋转和沿平面轴的位移。
Abaqus CAE中的此过程与对称条件的过程相同：
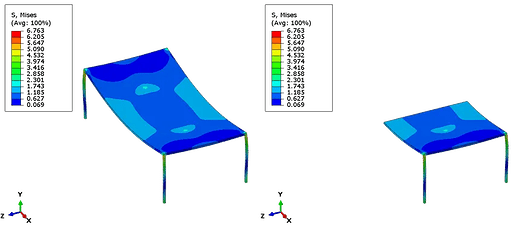
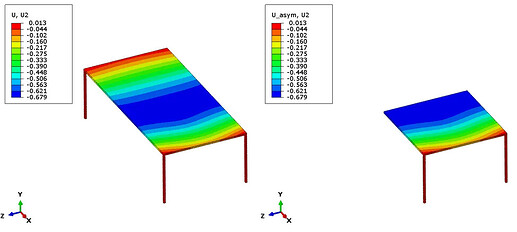
我们运行了具有反对称载荷和边界条件的相同桌子模型，如下所示。全模型与反对称模型的结果，虽然仔细想想，这对于一桌来说不太现实！另请注意，使用反对称条件无法在后处理进行可视化显示全模型。
不对称性
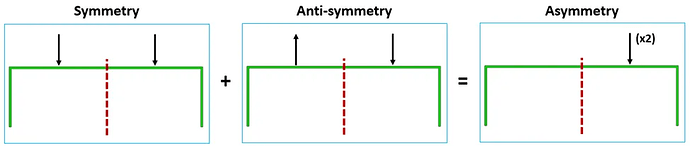
对称和反对称边界条件的一个巧妙特性是，在线性分析中，如果将具有对称和反对称边界的载荷工况添加在一起，载荷将会抵消。这使我们能够施加不对称载荷。
为了证明这一点，我们依旧使用了桌子示例 - 使用对称和反对称边界条件运行半个桌子模型，并将两者的应力和位移相加。这是与负载两倍的整张桌子进行比较的。正如我们在下图中看到的，结果是相同的。
请再次注意，无法使用此方法预测桌子的另一侧（未建模）的行为。只有被建模的一方才是相关的——并且没有适当的方法来估计另一半的行为。此外，如果模型中存在非线性，这种方法将不起作用。
轴对称
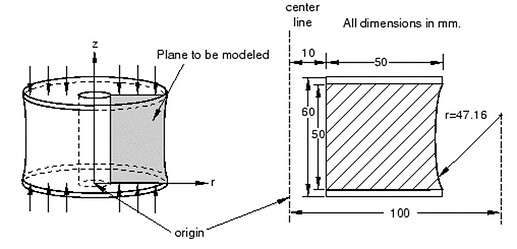
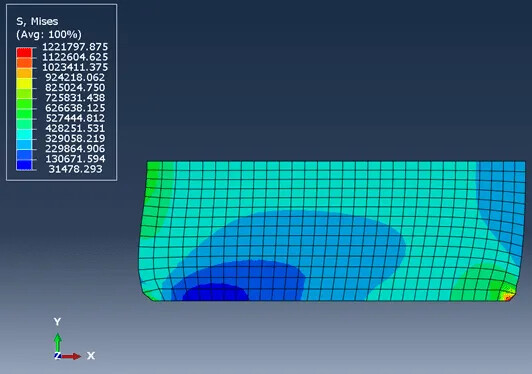
如果几何形状和载荷都是绕轴旋转一周，则可以使用轴对称（或简称轴对称）。例如，下图所示的安装座是关于中心轴轴对称的。不过，这次没有使用边界条件，而是使用了一种特殊的单元类型，即轴对称单元。使用它们，我们可以对安装座的横截面进行建模，而不是对整个安装座进行3D建模。这大大简化了分析。
轴对称单元是相对于对称轴建模的，因此径向方向不需要特定的边界条件。应用关于XZ平面的对称性来进一步简化模型，并将压力载荷施加到安装座的底部。
Abaqus单元形式为CAX，它是轴对称实体单元。边界条件和截面定义等模型特征的工作方式就像3D实体单元一样，但模拟以2D运行。
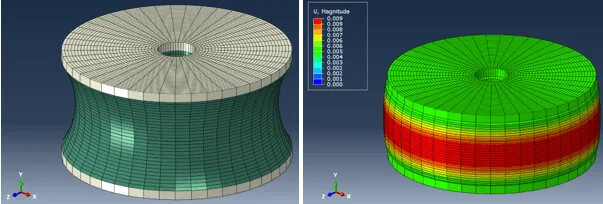
我们可以使用“ODB显示选项”中的扫描/拉伸和镜像/图案选项来查看安装座的完整形状：
注意事项
对称性不应用于模态分析或屈曲分析等模态不一定对称的情况。
最后
简而言之，对称性可以成为帮助简化FEA模型并减少运行时间的出色工具。我们建议在适用的情况下使用它。