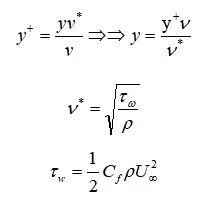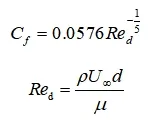定义
因为流体无论流动,还是传热、传质都存在边界层。而之所以有壁面函数这个东西,根源就在于边界层理论。
边界层理论
边界层分为速度边界层、热边界层和浓度边界层。
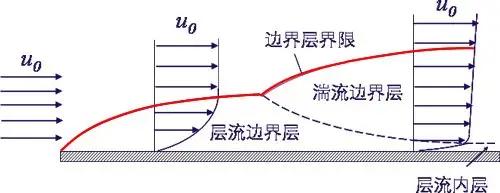
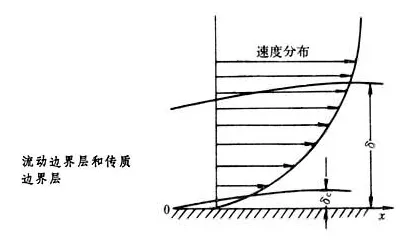
速度边界层:当具有粘性的流体,经过壁面附近,流速下降,直接贴附于壁面的流体静止不动的一个薄层。
![]()
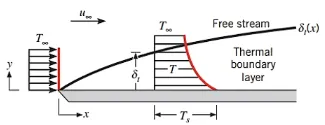
热边界层:指黏性流体流动壁面附近形成的以温度剧变为特征的流体薄层。
热边界层厚度:
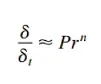
其中 δ 表示速度边界层的厚度,δ_t 表示热边界层的厚度
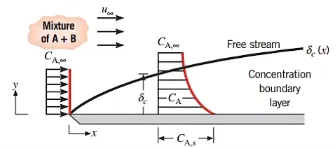
浓度边界层:某组分在流体中的浓度与固体壁面的浓度存在差异,则在壁面垂直方向上的流体内部将存在浓度梯度的流体薄层。
浓度边界层厚度:
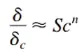
其中 δ 表示速度边界层的厚度,δ_c 表示热边界层的厚度。
近壁面细节捕获
三种边界层都有一个共同的特点:某个物理量A发生剧变,在边界层内产生非常大的梯度,且越靠近边界层梯度越大。而在边界层外,物理量A与主流中的物理量A值几乎相等,不存在梯度。
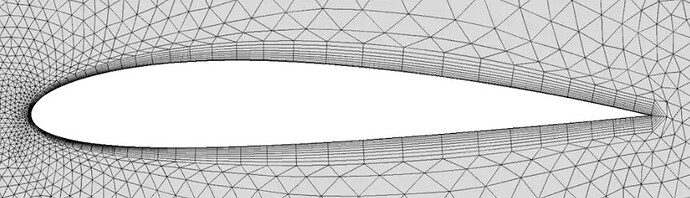
为了获得更加精确的计算结果,必须对边界层内的物理量梯度进行非常细节的捕获——网格加密
边界层网格加密将边界层网格画的非常密,越靠近边界层网格越密,这样可以捕获更多的细节,同时计算也会更加准确。
但是边界层网格加密存在两个缺点:
-
网格数量大大增加,为了获取更多的细节,需要不断细化网格,计算时间大大加长;
-
网格质量变差,边界层网格的加密,导致网格的纵横比非常大,甚至达到上百,高纵横比可能会导致计算难以收敛,甚至发散。
湍流边界层的壁面律
有没有既不需要划分更多的网格,同时还能捕获更多的边界层细节?
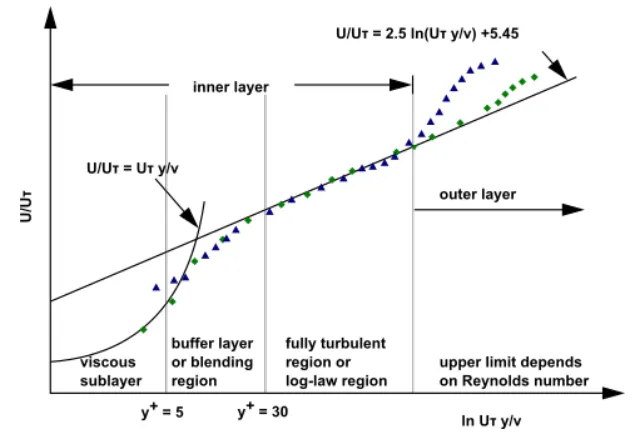
通过对边界层的研究,将边界层分为了三个区域,分别为粘性底层(0< y^+ <5)、缓冲层(5< y^+ <30)和完全湍流层( y^+ >30)。
这里用两个无量纲物理量 u^+ 和 y^+ 来定义边界层内的规律更具有普遍性。
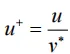
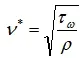
u^+ 表示无量纲速度,u 表示边界层内流体速度,τ_w 为壁面切应力
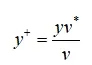
y^+ 表示到壁面处的无量纲距离,y 表示边界层某点到壁面的距离,v 表示流体运动粘度 m^2/s 。
对边界层这三个区域进行了大量的实验,结果表面这三个区域内u+和y+的规律不同。
对于粘性底层(0< y^+ <5),u^+ 与 y^+ 近似呈线性关系;
对于完全湍流层,u^+ 与 y^+ 近似呈对数关系,被称为对数律;
对于缓冲层,线性关系曲线和对数律曲线在缓冲层有交点,交点所对应的 y^+ 值在11附近。
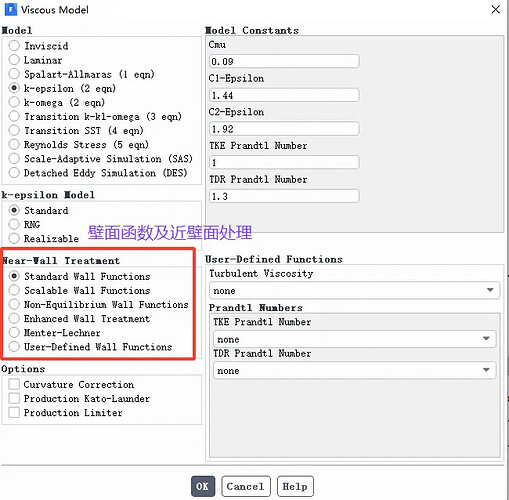
壁面函数
壁面函数的概念
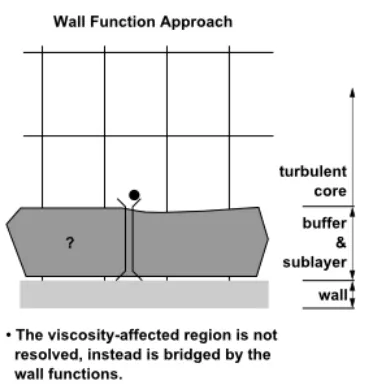
Fluent软件提供了一种被称为壁面函数的方式来实现上述的思想。壁面函数是一种半经验公式,被用来连接壁面和完全湍流区域之间的粘性影响区域。
壁面函数以对数律为基础来计算边界层规律,其忽视了粘性底层和缓冲层。因此画边界层网格时不能画出粘性底层和缓冲层,而要直接画到完全湍流层。
也就是说使用壁面函数,不但不需要在边界层内细化网格,反而必须要保证第一层网格处于对数律能够应用的范围。
通常将即 y^+=15 处作为可以使用对数律的分界线,所以第一层网格要保证 y^+>15 。第一层网格大小可以由下式推导:
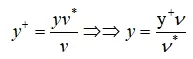
Fluent使用另一种无量纲速度 U^* 和无量纲距离 y^* 来描述边界层内的规律
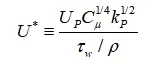
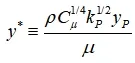
u^+ ,y^+ 与 U^* ,y^* 在湍流边界层中近似相等,应用时直接用 u^+ ,y^+ 即可。
使用壁面函数确实简化了边界层的网格,但是也忽略了粘性底层和缓冲层,因此壁面函数的方法适用于粘性底层数据不重要的求解。
如果要研究的就是粘性底层的数据,如边界层分离现象,那么壁面函数的方法不适用了。Fluent提供了另外一种方式用于求解粘性底层。
y^+ 的确定
为了留出一定的余量保证计算结果的准确性,Fluent要求 y^+ 必须大于15,如果 y^+ 小于15,Fluent就无法保证求解的准确性。y^+ 的下限为15,上限则取决于雷诺数。
对于高雷诺数:如轮船,飞机等,对数律范围扩大,y^+ 上限可以取到几千,减少网格数量;
对于低雷诺数:如涡轮叶片等,y^+ 上限可以取到100;
对于很低的雷诺数:对数律范围很窄,为了保证 y^+ >15,可能会使边界层网格层数很少,计算结果变差,因此不建议使用壁面函数。
相较于纠结 y^+ 的选取,边界层的网格层数足够时,能得到更精确的数值结果。
对于非结构网格,边界层网格层数在10-20之间,对于边界层Prism棱柱层网格,要保证边界层内至少15个节点。
边界层厚度
想要在边界层内画足够数量的网格,需要知道边界层的厚度。
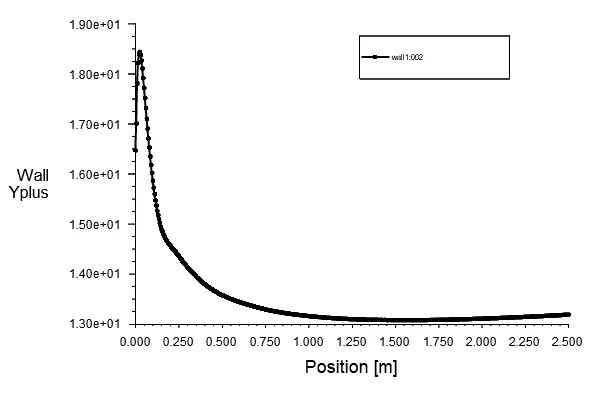
Fluent提供了一种估算方法。当大致划分网格进行计算得到一个求解结果时,可以在后处理查看turbulent viscosity湍流粘度物理量。
Results-Plots-XY plot
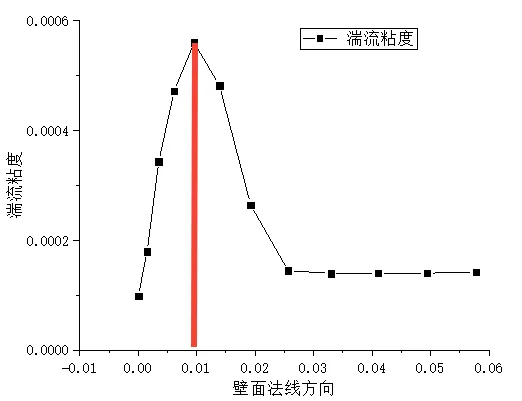
在垂直壁面方向画出turbulent viscosity沿垂直壁面方向的曲线图,turbulent viscosity的最大值出现在边界层的中间,最大值出现位置的2倍即为边界层的厚度。
比如下图为文章后源文件案例的湍流粘度,在x=0.01m处达到最大值,可以认为边界层厚度为0.02m。
对于某些特殊工况,边界层厚度也可以由理论公式推导出来。
估算边界层第一层网格
边界层第一层网格如何确定?当我们在Fluent中选择壁面函数时,必须要保证 y^+ >15。
由此可一步步反推第一层网格高度 y 的值。式中 ρ 为流体密度,U 为流体主流速度,U_∞ 为流体动力粘度,d 为特征长度。
估算雷诺数 Re
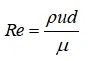
估算壁面摩擦系数
![]()
估算壁面剪切应力
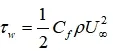
估算 v^*

计算边界层第一层网格
![]()
以上流程化的东西都可以通过编程实现。
进行一定的验证后发现,似乎是由于Fluent基于有限体积法,因此上述求出的第一层网格高度y实际上只是网格中心到壁面的距离,真正的第一层网格高度应该为此值的2倍。