I. Strength
Definition:
The ability of a component or part to resist failure (fracture) or significant deformation under the action of external forces.
For example, if Sun Yue uses an iPad as a scale and stands on it, causing the screen to crack, this is a case of insufficient strength. Similarly, during the annual summer floods in Wuhan, many large tree branches are broken by the wind, which is also a sign of insufficient strength.
Strength is a parameter that reflects the material’s resistance to fracture and other forms of failure. Strength generally includes tensile strength, compressive strength, etc., which is the amount of stress at which the material fails. The unit of strength is generally megapascals (MPa).
-
Types of Failure
- Brittle Fracture: Sudden fracture without significant plastic deformation. For instance, the fracture of cast iron specimens along the cross-section during tension and along the diagonal section during torsion of round-section cast iron specimens.
- Plastic Yielding: The material undergoes significant plastic deformation, causing the component to lose its working capacity. For example, low-carbon steel samples undergo significant plastic deformation during both tension and torsion.
-
Theories of Strength
- Maximum Tensile Stress Theory: If the maximum tensile stress \sigma _{1} at a point in a component reaches the limit stress \sigma _{b} in uniaxial stress state, the material will undergo brittle fracture. Therefore, the condition for brittle fracture failure of a component under complex stress state is: σ_{1} =σ_{b} . Thus, the strength condition established by the first strength theory is: σ_{1 } ≤ [σ].
- Maximum Tensile Strain Theory: If the maximum tensile strain \varepsilon _{1} reaches the limit value \varepsilon _{u} in uniaxial stress state, the material will undergo brittle fracture failure, \varepsilon _{1} =\varepsilon _{u} . From the generalized Hooke’s law, we get: \varepsilon _{1} =[\sigma _{1} -u(\sigma _{2} +\sigma _{3} )]/E, so \sigma _{1} -u(\sigma _{2} +\sigma _{3} )=\sigma _{b} . The strength condition established by the second strength theory is: \sigma _{1} -u(\sigma _{2} +\sigma _{3} )\le [\sigma ].
- Maximum Shear Stress Theory: If the maximum shear stress \tau _{max} reaches the limit shear stress \tau _{0} in uniaxial stress state, the material will undergo yielding failure. \tau _{max} =\tau _{0} . According to the stress formula on the oblique section of axial tension, \tau _{0} = \sigma _{s} /2 (\sigma _{s} is the normal stress on the cross-section). From the formula, we get: \tau _{max} =(\sigma _{1} -\sigma _{3} )/2. Therefore, the failure condition is rewritten as \sigma _{1} - \sigma _{3} = \sigma _{s} . The strength condition according to the third strength theory is: \sigma _{1} - \sigma _{3} \le \left [ \sigma \right ] .
- Distortion Energy Theory: If the distortion energy at a point in a component reaches the limit value under uniaxial stress state, the material will undergo yielding failure. Thus, the strength condition according to the fourth strength theory is:
\sqrt{\sigma _{1}^{2}+\sigma _{2}^{2}+\sigma _{3}^{2}-\sigma _{1} \sigma _{2} -\sigma _{2} \sigma _{3} -\sigma _{3} \sigma _{1} } < [\sigma ]
II. Stiffness
Definition:
The ability of a component or part to resist elastic deformation or displacement under the action of external forces, meaning that elastic deformation or displacement should not exceed the engineering allowable range.
Stiffness is a parameter that reflects the relationship between structural deformation and the magnitude of force, i.e., how much deformation a structure undergoes under a certain amount of force. Simply put, for a spring, the force divided by the elongation is the stiffness of the spring. The unit of stiffness is generally Newtons per meter (N/m).
-
Types of Stiffness
- When the applied load is a constant load, it is called static stiffness; when it is an alternating load, it is called dynamic stiffness. Static stiffness mainly includes structural stiffness and contact stiffness, where structural stiffness refers to the stiffness of the component itself, mainly including bending stiffness and torsional stiffness.
Bending stiffness is calculated as follows:
K= \frac{p}{\delta }
where P is the static load (N), and \delta is the elastic deformation in the direction of the load (μm).Torsional stiffness is calculated as follows:
K_{m} = \frac{ML}{\theta }
where M is the applied torque (N·m), L is the distance from the torque application point to the fixed end (m), and θ is the angle of twist (°).
III. The Connection Between the Two
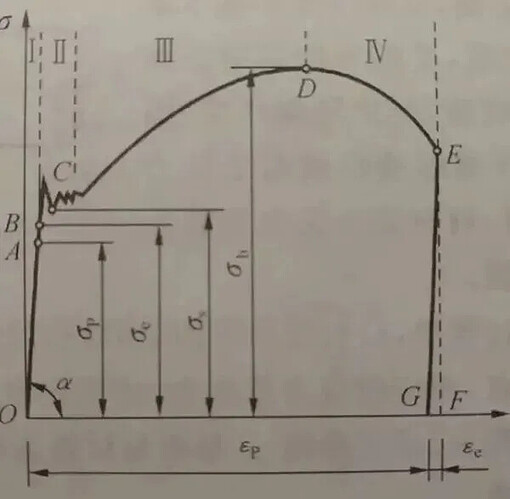
Through the understanding of the above theories on strength and stiffness, compared to stiffness, the definition of strength is aimed at failure under the action of external forces; and the classification of failure types includes plastic yielding and brittle fracture, which leads to the stress-strain curve during tension. As shown in the figure.
The curve in the figure can be divided into four stages:
I. Elastic deformation stage;
II. Yielding stage;
III. Hardening stage;
IV. Local necking stage.
The definition of stiffness is to resist elastic deformation, which occurs in the first stage, and under elastic action, Hooke’s law is satisfied. Observing the calculation formulas for bending stiffness and torsional stiffness under static load, similar to Hooke’s law, it can be inferred that the measurement of stiffness only occurs in the elastic deformation stage.
After entering the next stage, for the plastic strain or residual strain during the tensile process, it will not disappear. Under the stress-strain curve, the stress remains almost unchanged, while the strain increases significantly. At this point, the stress is the yield limit, and for the material, it has entered the plastic yielding failure stage. After entering the hardening stage, the strain increases with the increase of stress, and finally reaches the strength limit. It can be seen that the measurement of strength is between the elastic deformation of the material and the strength limit.
In summary, both stiffness and strength are measured values for the failure stage of parts, and stiffness can be measured by stress, while strength can be measured by deformation. In the strain process, stiffness is in the earlier stage, and strength is in the later stage. Therefore, in the measurement of part failure conditions, as long as the stiffness requirements are met, enough stress can be resisted in the elastic deformation stage, and strength also meets the requirements of the part under such conditions. According to this relationship, there are various designs in actual production, such as shafts in mechanical equipment, which are usually determined by strength conditions first, and then stiffness checks are carried out according to stiffness conditions. The stiffness requirements for shafts in precision machinery are also set very high, and their cross-sectional size design is often controlled by stiffness conditions.