Common Errors and Solutions in Fluent

[Max]

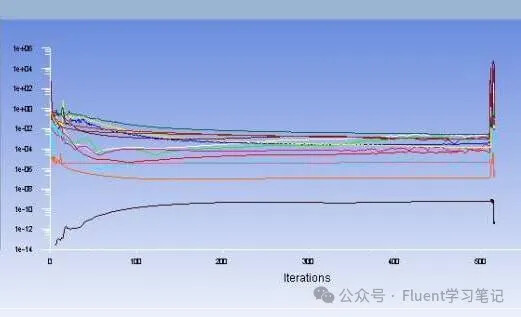
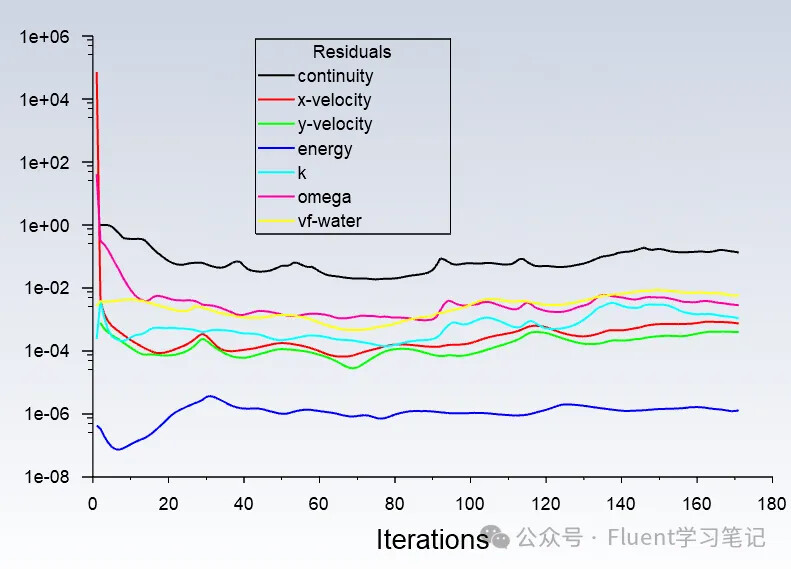
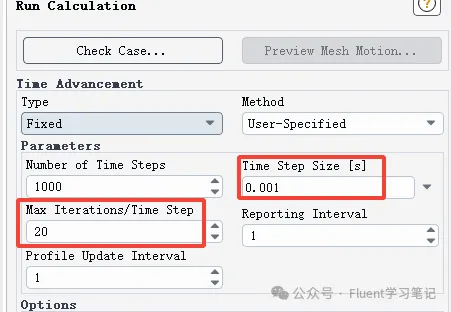
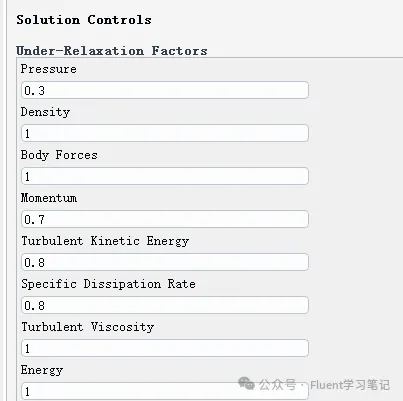
The convergence behavior in Fluent is often similar, but divergence situations can vary widely. Sometimes, rather than getting caught up in how to achieve convergence, it’s more useful to understand what to do if divergence occurs.

In the following sections, we will discuss several scenarios that often arise during calculations. Many times, these situations do not indicate true divergence but are common issues encountered during the computation process. Many students are unsure of how to address these problems or whether they can continue the calculation, and if they do, whether the results will be accurate. This article will provide a detailed overview to help clarify these concerns.

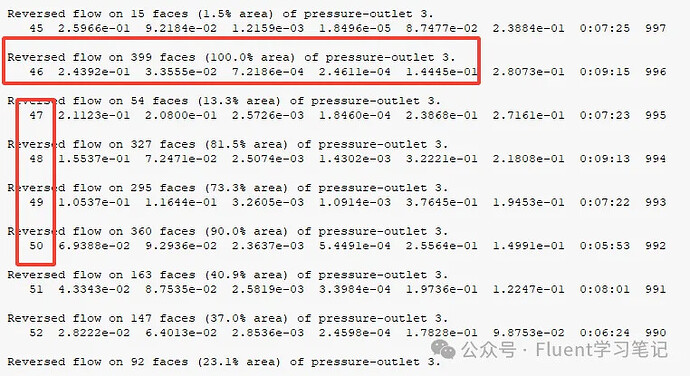
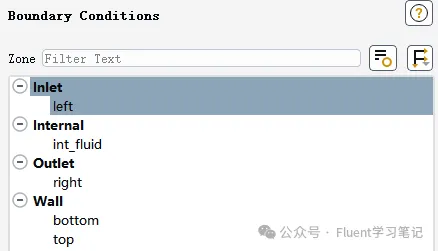
Problem 1: Outlet Backflow

• 1 出口回流介绍
  Reversed flow on 16 faces (4.1% area) of pressure-outlet 3
  
  
  
  Outlet backflow is a common occurrence in simulations. It refers to a situation where fluid that is supposed to exit the model through the outlet instead flows back into the computational domain. This is clearly inconsistent with the physical reality of the scenario.
  
  
  
  The occurrence of outlet backflow can generally be categorized into three types:

1. Initial Backflow During Calculation:

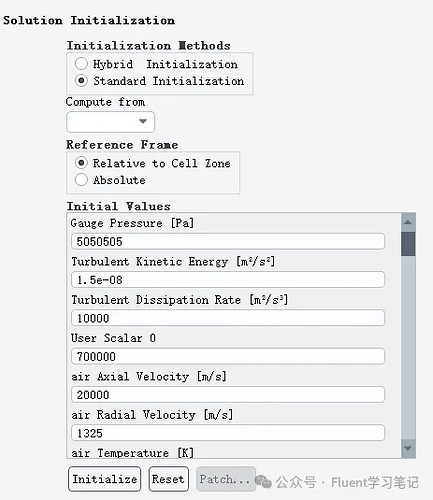
• This situation arises at the beginning of the simulation when the flow conditions are still settling. It may occur if the initial conditions are not set appropriately, leading to instability. To address this, ensure that initial conditions are physically realistic and closer to the expected flow state.

2. Unreasonable Physical Model:

• If the physical model or boundary conditions do not accurately represent the real-world scenario, backflow may occur. This can happen if the geometry is not modeled correctly, or if the flow rates and pressures do not match the physical reality. Reviewing and revising the physical model and boundary conditions can help resolve this issue.

3. Divergence in Calculations:

• Divergence indicates that the numerical solution is unstable, often resulting in erratic flow behavior and backflow. This can happen due to inadequate mesh quality, incorrect solver settings, or inappropriate relaxation factors. To mitigate divergence, consider refining the mesh, adjusting solver settings, and ensuring that boundary conditions are correctly defined.

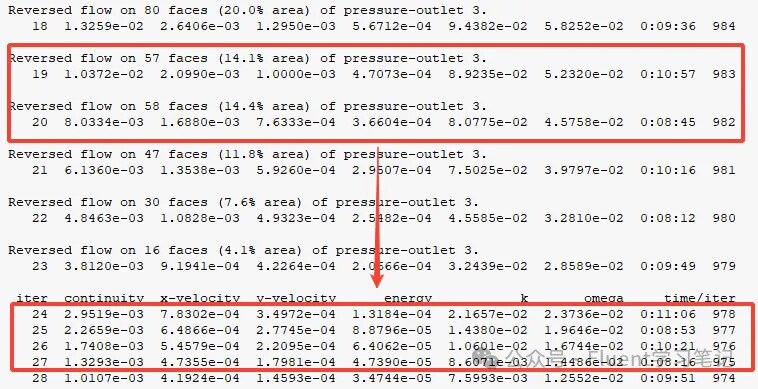
• 2. Initial Backflow During Calculation
  When starting a calculation and only running a few dozen steps, the occurrence of backflow is normal. As long as you continue the simulation, this phenomenon will eventually disappear.
  

  

• 3. Unreasonable Physical Model
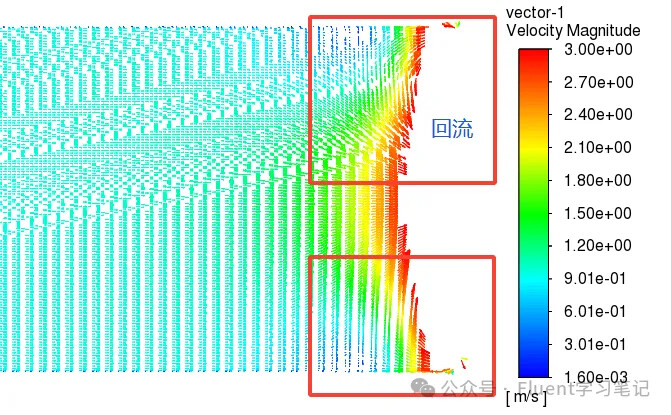
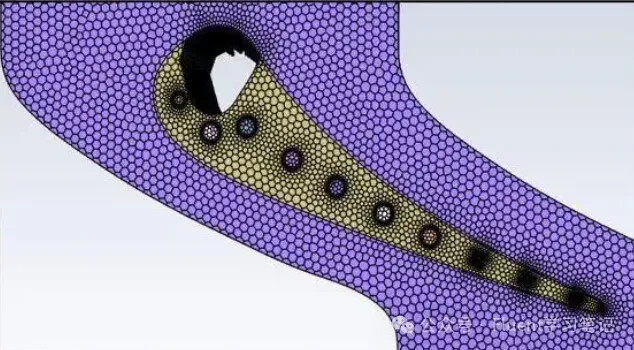
  If there are issues with the modeling, this situation can also arise. Even if the simulation continues running, the backflow phenomenon may not disappear, typically due to problems with the physical model. For instance, if the tail of the Kármán vortex street is too short and vortices are still present at the outlet, then backflow at the outlet is a normal occurrence.
  

  
  
  To resolve this issue, adjustments to the physical model are necessary, such as increasing the length of the wake region.
  
  

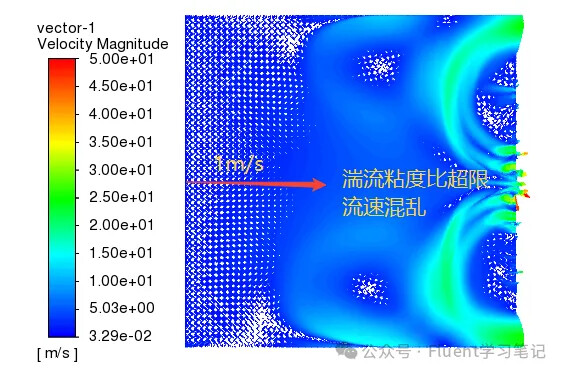
• 4. Divergence in Calculations
  The last situation is indeed divergence, where the velocity fluctuations in the flow field during the calculation are too significant. This can lead to numerical instability and prevent convergence.
  

  
  
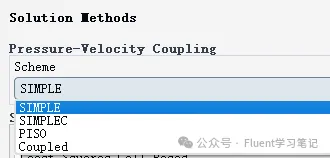
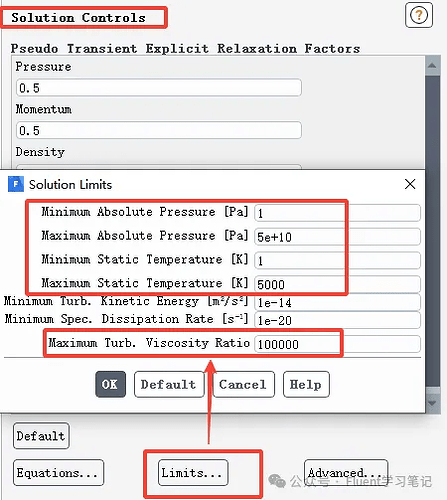
  At this point, the only option is to check the settings individually. The most common causes of divergence include:

1. Inappropriate Boundary Conditions: Ensure that all boundary conditions are defined correctly and realistically to match the physical scenario.
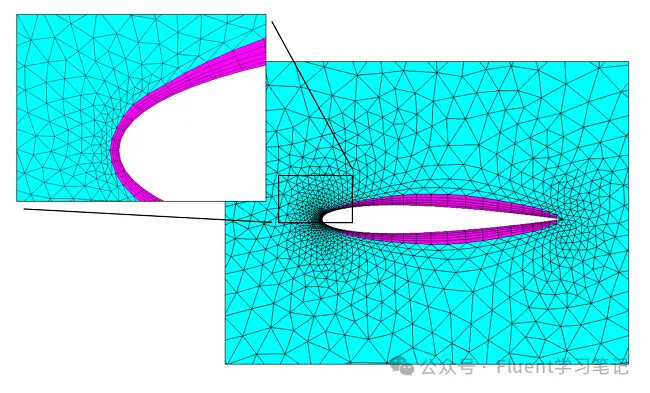
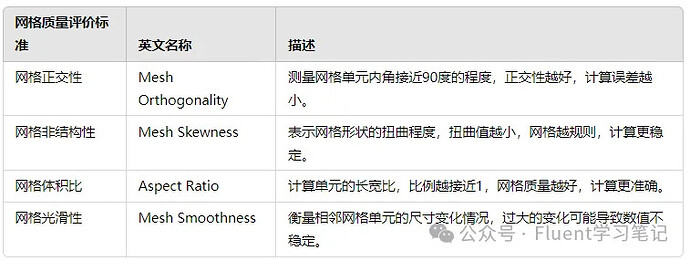
2. Poor Mesh Quality: Examine the mesh for issues such as high skewness or low quality in critical areas. Improving the mesh can enhance numerical stability.
3. Inadequate Selection of Mathematical Models: Verify that the chosen mathematical models (e.g., turbulence models) are suitable for the flow characteristics and conditions being simulated.

[Max]

3. Troubleshooting Divergence Issues

For divergence issues, you can refer to the following common troubleshooting steps and solutions:

3.1 Check Initial and Boundary Conditions

Ensure that all initial and boundary conditions are set reasonably. For example, values for velocity, pressure, and temperature should be physically plausible. If these conditions are set too high or too low, they may cause instability during the calculation.

Try using initial conditions that are closer to reality, or start with simple initial conditions, such as zero initial fields or smoother conditions.

3.2 Improve Mesh Quality

Check the quality of the mesh, especially parameters such as volume, skewness, and minimum cell size. Poor mesh quality may lead to numerical instability during calculations.

3.3 Adjust Calculation Settings

If performing transient calculations, try reducing the time step to make the computation more stable. In transient calculations, increase the number of iterations per time step to ensure each step converges sufficiently.

For steady-state calculations, reduce the relaxation factor to mitigate divergence.

3.4 Verify Physical Properties

Check and ensure that physical property parameters (such as density, viscosity, thermal conductivity, etc.) are set reasonably and make physical sense. In particular, changes in physical properties in multiphase flows or high-temperature, high-pressure environments may lead to instability.

3.5 Change Solver Settings

If convergence is poor with a double-precision solver, consider switching to a single-precision solver. Conversely, if a single-precision solver has poor convergence, try switching to a double-precision solver. Generally, double-precision solvers tend to improve calculation accuracy and reduce numerical errors.

You can also experiment with different pressure-velocity coupling algorithms (e.g., SIMPLE, PISO, Coupled) to test the stability of various methods.

3.6 Gradually Simplify the Problem

Try simplifying the model by removing physical models, simplifying geometric structures, or reducing the physical quantities being solved to see if convergence can be enhanced.

For example, only solving the flow field while ignoring heat or mass transfer can help determine if issues persist. This approach is often referred to as solving only part of the equations to enhance convergence.

3.7 Check UDFs

If User-Defined Functions (UDFs) are used and divergence issues arise, try removing the UDF to see if divergence persists. If the divergence disappears, it indicates an issue with the UDF, necessitating a review of the UDF code.

[Max]

Problem 2: Turbulent Viscosity Ratio Exceeded

1. Turbulent Viscosity Ratio Exceeded

When the console displays: “turbulent viscosity limited to viscosity ratio of 1.000000e+05 in 157607 cells,” it indicates that the turbulent viscosity ratio has been exceeded.

1.1 Understanding Turbulent Viscosity Ratio Exceeded

The term “turbulent viscosity ratio exceeded” refers to the situation where turbulent viscosity has reached the maximum value set internally by Fluent, which is 1.0×10⁵. If the turbulent viscosity ratio exceeds this value during calculations, it will be capped at this limit, and an informational message will appear.

For instance, the previous message indicates that in 157,607 cells in the computational domain, the turbulent viscosity ratio exceeded the 1.0×10⁵ limit. At this point, the turbulent fluid is likely problematic.

Since the value is simply too high, could it be that the actual value is indeed this high? In other words, it might not be a divergence issue, but this limit is already excessively large.

For example, in Fluent, the temperature limit is 1K-5000K. In physics, are there situations below 1K or above 5000K? Certainly, but those situations are very extreme; if truly outside this temperature range, Fluent is not suitable for simulation.

1.2 Occurrence at the Beginning of Calculation

Similar to the occurrence of outlet backflow, it is normal for the turbulent viscosity ratio to exceed limits at the beginning of the calculation. Generally, continuing the computation will make this phenomenon disappear, and no action is required.

1.3 Occurrence During Calculation Divergence

If this issue arises in the middle of the computation, it usually indicates that divergence has occurred. You can check the following aspects:

• Mesh Quality Issues: Poor mesh quality may lead to inaccurate turbulent model calculations, resulting in abnormally high turbulent viscosity ratios. Optimize mesh quality, especially near boundary layers.
  

  

• Improper Boundary Condition Settings: Incorrect boundary condition settings may result in unrealistic flow conditions in the computational domain, triggering the turbulent viscosity ratio exceedance.
  

  

• Solver Settings Issues: In some cases, using a segregated solver may lead to incorrect turbulent parameter calculations. Consider trying a coupled solver.
  

  

• Inappropriate Model Selection: For certain complex flow situations, it may be necessary to use more advanced turbulent models, such as the Reynolds Stress Model (RSM), rather than standard k-epsilon or k-omega models.
  

  

[Max]

Problem 3: Temperature and Pressure Exceeding Limits

In addition to the turbulent viscosity ratio exceeding limits, the text control box may also display temperature limit warnings, such as: “temperature limited to 5.000000e+03 in 159201 cells on zone 4.”

Similar to the reasons for turbulent viscosity exceedance, Fluent has internal range limits for temperature, pressure, turbulent kinetic energy, and turbulent kinetic energy dissipation rate. If these limits are exceeded, an informational message will appear.

The Limits interface under Solution Controls displays these physical quantity limits, which can also be modified.

The solutions are similar to those for turbulent viscosity ratio exceedance. If it occurs at the beginning of the computation, consider whether the initialization parameters are set correctly, and continue calculating to see if this phenomenon disappears.

If it occurs in the middle of the computation, possible causes include mesh quality issues, improper boundary condition settings, solver settings problems, and inappropriate model selection. Refer to the solutions provided for turbulent viscosity ratio exceedance.

[Max]

Problem 4: Floating Point Exception

1. Floating Point Exception Overview

Floating point exceptions are one of the most common non-convergence issues. The text control bar will display the following message: “Error: floating point exception.”

Fluent will then stop the calculation. Do not hold any false hopes; your current calculation has diverged to the point where Fluent deems it unnecessary to continue.

1.2 Why Does Floating Point Exception Occur?

In essence, a floating point exception is a computer term that refers to errors that occur during floating point calculations. Floating point exceptions typically include the following situations:

• Division by Zero: Attempting to divide by zero will trigger a floating point exception. Mathematically, division by zero is undefined, leading to an error in computation.
  

  

• Overflow: When the result of a calculation exceeds the maximum or minimum value that a floating point number can represent, an overflow occurs. The absolute range of double precision numbers is approximately -1.79E+308 to +1.79E+308. For example, multiplying a very large number by itself multiple times may lead to overflow.
  

  
  
  
  

• Underflow: When the result of a calculation is very close to zero and cannot be represented with current precision, underflow occurs. In such cases, the result may be set to zero.

• Invalid Operations: Certain operations are mathematically undefined, such as the square root of a negative number or operations involving incorrectly formatted numbers (like NaN, or “not a number”).
  

  

1.3 Solutions for Floating Point Exceptions

It can be confirmed that the occurrence of a floating point exception indicates divergence, and the only option is to recalculate. You cannot continue on the original basis. In fact, even if you attempt to recalculate from the original basis, it won’t work.

Finding the exact reason for floating point exceptions during the Fluent calculation process is not easy, and you can only check the settings one by one as you would for divergence. For divergence, you can refer to the common troubleshooting steps and solutions outlined above:

1. Check Initial and Boundary Conditions: Ensure all initial and boundary conditions are set reasonably. For example, velocity, pressure, and temperature values should be physically plausible. If these conditions are set too high or too low, they may cause instability during the calculation.
   

   

2. Improve Mesh Quality: Check the quality of the mesh, especially parameters such as volume, skewness, and minimum cell size. Poor mesh quality (e.g., highly distorted mesh) may lead to numerical instability during calculations.
   

   

3. Adjust Calculation Settings: If performing transient calculations, try reducing the time step to make the computation more stable. In transient calculations, increase the number of iterations per time step to ensure sufficient convergence for each step.
   

   
   
   
   

4. Verify Physical Properties: Check and ensure that physical property parameters (such as density, viscosity, thermal conductivity, etc.) are set reasonably and make physical sense. This is especially important in multiphase flows or high-temperature, high-pressure environments, where variations in physical properties may lead to instability.
   

   

5. Change Solver Settings: If convergence is poor with a double-precision solver, consider switching to a single-precision solver. Conversely, if a single-precision solver has poor convergence, try switching to a double-precision solver. Generally, double-precision solvers tend to improve calculation accuracy and reduce numerical errors.
   

   
   
   
   

6. Gradually Simplify the Problem: Try simplifying the model by removing physical models, simplifying geometric structures, or reducing the physical quantities being solved to see if convergence can be enhanced.
   

   
   
   
   

7. If we are using a UDF and encounter a floating point overflow issue, we can try removing the UDF to see if the floating point overflow still occurs. If the overflow disappears, it indicates that the issue is related to the UDF, and we need to check the UDF code.

Note: The above solutions are general troubleshooting steps for divergence issues and are not exclusively for floating point overflow problems.

[Max]

Problem 5: Stabilizing Temperature to Enhance Linear Solver Robustness

1. Enhancing Linear Solver Robustness

The text control bar may also display the following messages:

• “Stabilizing temperature to enhance linear solver robustness.”
• “Stabilizing pressure using GMRES to enhance linear solver robustness.”

These messages often appear alongside floating point exceptions.

When only these messages appear, it typically indicates that the convergence is not good, or it’s during the initial stages of computation. You can generally ignore them for now and continue the calculation to see if this situation resolves itself.

If this issue persists, it indicates that the convergence is still not satisfactory, but it has not reached complete divergence yet. At this point, you need to adjust some computational settings to enhance convergence. Common approaches include reduc

ing the time step size or lowering the relaxation factor.