虚位移原理

[Max]

1 约束及其分类

将限制所研究物体位移的周围物体称为该物体的约束。

事实上， 这种限制作用完全可以用一定的数学关系式进行表述， 这样在后续的分析工作中更便于应用。现将约束定义为：限制质点或质点系运动的关系式称为约束，若这些关系式可以用等式来表述， 则称之为约束方程。

1.1 几何约束和运动约束

图 1

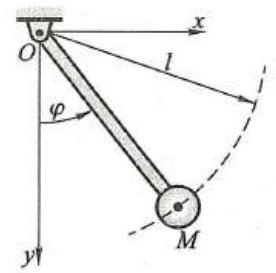
限制质点或质点系在空间中的几何位置的关系式称为几何约束。如图 1 所示，质点 M 可绕固定点 O 在平面 {Oxy} 内摆动，其摆长为 l，若以 x\text{、}y 表示质点的坐标，则其约束方程为

{x}^{2} + {y}^{2} = {l}^{2} \tag{1}

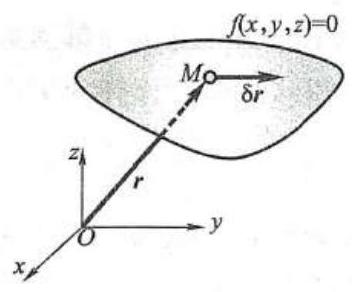
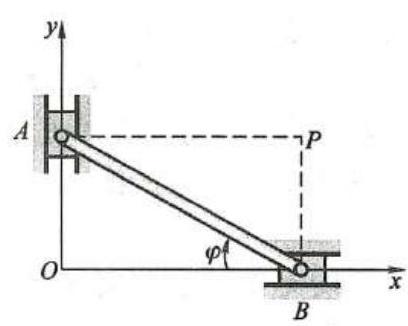
又如，质点 M 在图 2 所示固定曲面上运动，那么曲面方程就是质点 M 的约束方程。在图 3 所示曲柄连杆滑块机构中，连杆 {AB} 所受约束有: 点 A 只能做以点 O 为圆心、以 r 为半径的圆周运动，点 B 始终沿滑道做直线运动；点 B 与点 A 间的距离始终保持为杆长 l 。这三个条件以约束方程表示为

\left. \begin{array}{l} {x}_{A}^{2} + {y}_{A}^{2} = {r}^{2} \\ {y}_{B} = 0 \\ {\left( {x}_{B} - {x}_{A}\right) }^{2} + {\left( {y}_{B} - {y}_{A}\right) }^{2} = {l}^{2} \end{array}\right\} \tag{2}

图 2

图 3

上述中各约束都是限制物体的几何位置， 因此都是几何约束。

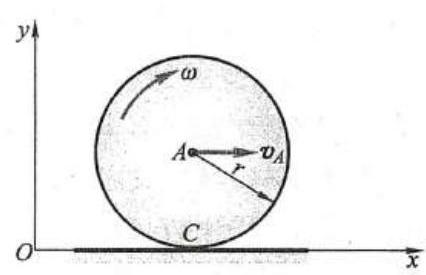
限制质点系运动情况的运动学条件， 称为运动约束。如图 4 所示， 车轮沿直线轨道做纯滚动，车轮除了受到限制其轮心 A 始终与地面保持距离为 r 的几何约束 {y}_{A} = r 外，还受到只滚不滑的运动学的限制， 即在每一瞬时， 有

{v}_{A} - {r\omega } = 0

图 4

上述约束关系式就是运动约束。设 {x}_{A} 为轮心 A 的 x 坐标， \varphi 为车轮的转角，由 {v}_{A} = {\dot{x}}_{A}，\omega = \dot{\varphi }，上式可以写成

{\dot{x}}_{A} - r\dot{\varphi } = 0

若 r 为常数，上式两端可以对时间积分，得到

{x}_{A} - {x}_{A0} = r\left( {\varphi - {\varphi }_{0}}\right)

其中， {x}_{A0}\text{、}{\varphi }_{0} 为 {x}_{A}\text{、}\varphi 在 t = 0 时的值。这样约束方程就转化为以质点系位置坐标表示的几何约束方程。这类约束称为可积分的运动约束。显然可积分的运动约束等同于几何约束。

1.2 定常约束和非定常约束

图 5 中重物 M 由一根穿过固定圆环 O 的细绳系住。设摆长在开始时为 {l}_{0}，然后以不变的速度 v 拉动细绳的另一端，此时单摆的约束方程为

{x}^{2} + {y}^{2} \leq {\left( {l}_{0} - vt\right) }^{2} \tag{3}

图 5

由上式可见， 约束条件是随时间变化的， 这类约束称为非定常约束。

不随时间变化的约束称为定常约束， 在定常约束的约束方程中不显含时间 t，如式 (1) 所示的约束方程。

1.3 双侧约束和单侧约束

在图 1 所示单摆的例子中， 摆杆是一刚性杆， 它限制质点沿杆的拉伸方向的位移， 又限制质点沿杆的压缩方向的位移， 这类约束称为双侧约束 (或称为固执约束)，双侧约束的约束方程是等式，例如式 (1)。而图 5 所示的单摆是用绳子系住的，而绳子不能限制质点沿绳索缩短方向上的位移，这类约束称为单侧约束，其约束关系式为不等式，例如式 (3)。

1.4 完整约束和非完整约束

由几何约束和可积分的运动约束所组成的这类约束称为完整约束。若运动约束关系式中包含的微分项不能积分成有限形式， 则这类约束称为非完整约束。其约束方程的一般形式为

{f}_{j}\left( {{x}_{1},{y}_{1},{z}_{1};{x}_{2},{y}_{2},{z}_{2};\cdots ;{x}_{n},{y}_{n},{z}_{n};t}\right) = 0\;\left( {j = 1,2,\cdots,s}\right) \tag{4}

式中， n 为受约束作用的质点系中质点的个数， s 为约束方程的个数。

2 虚位移

在一般平衡问题中， 质点系中各质点都是静止不动的。为了应用功的概念分析质点系的平衡问题， 设想在约束允许的条件下， 给各质点一个微小的位移， 这些微小的位移是假想的， 与时间无关， 称为虚位移。

考虑由 n 个质点组成的质点系受 s 个完整、双侧约束作用而处于平衡状态。 设质点系中第 i 个质点的矢径为

{\mathbf{r}}_{i} = {x}_{i}\mathbf{i} + {y}_{i}\mathbf{j} + {z}_{i}\mathbf{k}

这里 {x}_{i}\text{、}{y}_{i}\text{、}{z}_{i} 为第 i 个质点的直角坐标， i\text{、}j\text{、}k 为沿三个坐标轴正向的单位矢量。 为了与动力学中质点经过 \mathrm{d}t 时间而产生的实际位移(简称实位移，通常用 \mathrm{d}{\mathbf{r}}_{i} 来表示) 相区别， 质点的虚位移表示为

\delta {r}_{i} = \delta {x}_{i}i + \delta {y}_{i}j + \delta {z}_{i}k \tag{5}

这里用来表示虚位移的符号 \delta 是变分符号，“变分”包含有无限小“变化”的意思。

设想给质点系一组虚位移，则第 i 个质点的矢径为

{\mathbf{r}}_{i}^{\prime } = {\mathbf{r}}_{i} + \delta {\mathbf{r}}_{i} = \left( {{x}_{i} + \delta {x}_{i}}\right) \mathbf{i} + \left( {{y}_{i} + \delta {y}_{i}}\right) \mathbf{j} + \left( {{z}_{i} + \delta {z}_{i}}\right) \mathbf{k} \tag{6}

将式(6)代入约束方程式(4)，注意虚位移的产生与时间无关，故 t 保持不变， 得到

{f}_{j}\left( {{x}_{1} + \delta {x}_{1},{y}_{1} + \delta {y}_{1},{z}_{1} + \delta {z}_{1};{x}_{2} + \delta {x}_{2},{y}_{2} + \delta {y}_{2},{z}_{2} + \delta {z}_{2};\cdots ;{x}_{n} + \delta {x}_{n},{y}_{n} + \delta {y}_{n},{z}_{n} + \delta {z}_{n};t}\right) = 0

将上式用泰勒级数展开，并代入式(4)，有

\mathop{\sum }\limits_{{i = 1}}^{n}\left( {\frac{\partial {f}_{j}}{\partial {x}_{i}}\delta {x}_{i} + \frac{\partial {f}_{j}}{\partial {y}_{i}}\delta {y}_{i} + \frac{\partial {f}_{j}}{\partial {z}_{i}}\delta {z}_{i}}\right) = 0\;\left( {j = 1，2，\cdots，s}\right) \tag{7}

因此， 虚位移又可以定义为质点系满足方程组 (7) 的任一组微小位移。

必须注意， 虚位移与实位移是不同的概念。实位移是质点系在一定时间内真正实现的位移， 它除了与约束条件有关外， 还与时间、主动力及运动的初始条件有关；而虚位移仅与约束条件有关。对于定常完整约束，真实位移是所有虚位移中的一组；对于非定常约束，某瞬时的虚位移是指将时间固定， 约束所允许的无限小位移，与真实位移无关。

在动力学中，常用 \mathrm{d}\mathbf{r} 来描述质点在 \mathrm{d}t 时间内产生的位移，所关注的是每个质点在力作用下的运动，即 \mathbf{r} = \mathbf{r}\left( t\right)，质点的运动方程可看成是时间 t 的单变量函数，采用的数学工具为函数的微积分；由于是平衡问题，所关注的是质点系中各质点在平衡状态下的位置与作用力之间的关系， 而式 (7) 正是通过虚位移来刻画质点系平衡位置的几何特性 (约束特性)， 所对应的数学工具为泛函的变分。

例 1 图 6 所示椭圆规机构中，连杆 {AB} 长为 l，在图示位置与水平线夹角为 \varphi，试求滑块 A\text{、}B 的一组虚位移。

解: 取坐标系如图所示，则滑块 A\text{、}B 应满足的约束方程为

\left. \begin{array}{l} {x}_{A} = 0 \\ {y}_{B} = 0 \\ {\left( {x}_{A} - {x}_{B}\right) }^{2} + {\left( {y}_{A} - {y}_{B}\right) }^{2} - {l}^{2} = 0 \end{array}\right\} \tag{a}

图 6

设滑块 A\text{、}B 的虚位移为

\left. \begin{array}{l} \delta {r}_{A} = \delta {x}_{A}i + \delta {y}_{A}j \\ \delta {r}_{B} = \delta {x}_{B}i + \delta {y}_{B}j \end{array}\right\} \tag{b}

由约束方程 (a)， 有

\left. \begin{array}{l} \delta {x}_{A} = 0 \\ \delta {y}_{B} = 0 \\ \left( {{x}_{A} - {x}_{B}}\right) \left( {\delta {x}_{A} - \delta {x}_{B}}\right) + \left( {{y}_{A} - {y}_{B}}\right) \left( {\delta {y}_{A} - \delta {y}_{B}}\right) = 0 \end{array}\right\} \tag{c}

即任意满足式 (c) 的 \delta {\mathbf{r}}_{A} 、 \delta {\mathbf{r}}_{B} 均为滑块 A 、 B 的一组虚位移。

2.1 虚功

质点或质点系所受的力在虚位移上所做的功称为虚功。设力 \mathbf{F} 作用点的虚位移为 {\delta r}，则虚功为

{\delta W} = F \cdot {\delta r}

应该指出虚位移只是假想的， 而不是真实发生的， 因而虚功也是假想的。力在虚位移上做功的计算与作用力在真实小位移上所做元功的计算是一样的。

2.2 理想约束

如果在质点系的任何虚位移中， 所有约束力所做虚功的和等于零， 这种约束称为理想约束。若以 {\mathbf{F}}_{\mathrm{N}i} 表示作用在质点 i 上的约束力， \delta {\mathbf{r}}_{i} 表示该质点的虚位移， \delta {W}_{\mathrm{{Ni}}} 表示该约束力在虚位移上所做的功，则理想约束可以用数学公式表示为

\delta {W}_{\mathrm{N}} = \sum \delta {W}_{\mathrm{N}i} = \sum {\mathbf{F}}_{\mathrm{N}i} \cdot \delta {\mathbf{r}}_{i} = 0 \tag{8}

在动能定理中说明光滑固定面、光滑铰链、无重刚杆、不可伸长的柔索、固定端等约束为理想约束，现从式(8)的定义来看，这一结论也是成立的。

3 虚位移原理

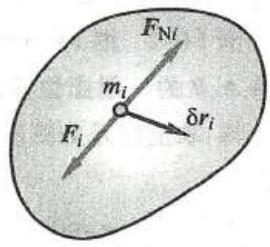
设有一质点系处于静止平衡状态，取质点系中任一质点 {m}_{i}，如图 7 所示， 作用在该质点上的主动力的合力为 {\mathbf{F}}_{i}，约束力的合力为 {\mathbf{F}}_{\mathrm{N}i} 。因为质点系处于平衡状态， 则这个质点也处于平衡状态， 因此有

{\mathbf{F}}_{i} + {\mathbf{F}}_{\mathrm{N}i} = \mathbf{0}

图 7

若给质点系以某种虚位移，其中质点 {m}_{i} 的虚位移为 \delta {\mathbf{r}}_{i}，则作用在质点 {m}_{i} 上的力 {\mathbf{F}}_{i} 和 {\mathbf{F}}_{\mathrm{N}i} 的虚功的和为

{\mathbf{F}}_{i} \cdot \delta {\mathbf{r}}_{i} + {\mathbf{F}}_{\mathrm{N}i} \cdot \delta {\mathbf{r}}_{i} = 0

对于质点系内所有质点， 都可以得到与上式同样的等式。将这些等式相加， 得

\sum {\mathbf{F}}_{i} \cdot \delta {\mathbf{r}}_{i} + \sum {\mathbf{F}}_{\mathrm{N}i} \cdot \delta {\mathbf{r}}_{i} = 0

如果质点系具有理想约束， 则约束力在虚位移上所做虚功的和为零， 即 \sum {\mathbf{F}}_{Ni} \cdot \delta {\mathbf{r}}_{i} = 0，代入上式得

\sum {\mathbf{F}}_{i} \cdot \delta {\mathbf{r}}_{i} = 0 \tag{9}

用 \delta {W}_{Fi} 代表作用在质点 {m}_{i} 上的主动力的虚功，由于 \delta {W}_{Fi} = {\mathbf{F}}_{i} \cdot \delta {\mathbf{r}}_{i}，则上式可以写为

\sum \delta{W}_{Fi} = 0 \tag{10}

可以证明， 上式不仅是质点系平衡的必要条件， 也是充分条件。

因此可得结论:对于具有理想约束的质点系，其平衡的充分必要条件是:作用于质点系的所有主动力在任何虚位移上所做虚功的和等于零。上述结论称为虚位移原理，又称为虚功原理，式(9)，式(10)又称为虚功方程。

式(9)也可写成解析表达式，即

\sum \left( {{F}_{ix}\delta {x}_{i} + {F}_{iy}\delta {y}_{i} + {F}_{iz}\delta {z}_{i}}\right) = 0 \tag{11}

式中， {F}_{ix}\text{、}{F}_{iy}\text{、}{F}_{iz} 为作用于质点 {m}_{i} 的主动力 {F}_{i} 在直角坐标轴上的投影；\delta {x}_{i}\text{、}\delta {y}_{i}\text{、}\delta {z}_{i} 为虚位移 \delta {\mathbf{r}}_{i} 在直角坐标轴上的投影。

以上证明了虚位移原理的必要性， 即若质点系平衡则式 (9) 必定成立。应该指出，式 (9) 也是质点系平衡的充分条件，即在满足式 (9) 的条件下，质点系必保持平衡状态。

考虑质点系初始处于静止平衡状态，若其受满足式(9)的力系作用而不再保持平衡，则经过 \mathrm{d}t 时间，必有某个处于非平衡状态的质点 i 由静止发生运动，且其位移应与该质点所受合力的方向相同(初始静止，质点沿运动轨迹的法向加速度为零)。对于定常、完整、双侧约束，这一微小位移也应满足该质点所受的约束条件，即该质点在 \mathrm{d}t 时间内的真实微小位移应为其虚位移之一，记为 \delta {\mathbf{r}}_{i} 。设作用在该质点上主动力的合力为 {\mathbf{F}}_{i}，约束力的合力为 {\mathbf{F}}_{\mathrm{N}i}，则必有不等式

\left( {{\mathbf{F}}_{i} + {\mathbf{F}}_{Ni}}\right) \cdot \delta {\mathbf{r}}_{i} > 0

这样处于非平衡状态的质点上作用力的虚功都大于零， 而保持静止的质点上作用力的虚功都等于零， 因而全部虚功相加仍为不等式， 即

\sum \left( {{\mathbf{F}}_{i} + {\mathbf{F}}_{\mathrm{N}i}}\right) \cdot \delta {\mathbf{r}}_{i} > 0

理想约束下， 有

\sum {F}_{Ni} \cdot \delta {r}_{i} = 0

由此得出

\sum {\mathbf{F}}_{i} \cdot \delta {\mathbf{r}}_{i} > 0

这与式 (9) 是矛盾的，由此说明原理的充分性成立。

应该指出， 虽然应用虚位移原理的条件是质点系应具有理想约束， 但是也可以用于有摩擦的情况，只要把摩擦力当作主动力，在虚功方程中计入摩擦力所做的虚功即可。

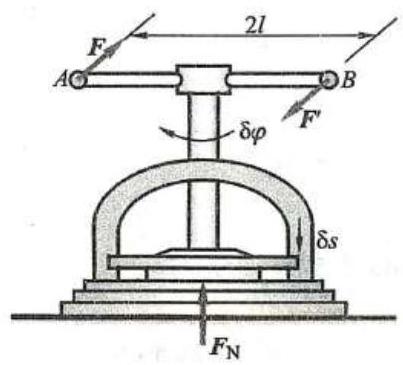
例 2 如图 8 所示，在螺旋压榨机的手柄上作用一在水平面内的力偶 \left( {F，{F}^{\prime }}\right)，其力偶矩 M = {2Fl}，螺杆的螺距为 h 。求机构平衡时加在被压榨物体上的力。

解:研究以手柄、螺杆和压板组成的平衡系统。忽略螺杆和螺母间的摩擦， 则约束是理想的。

图 8

作用于平衡系统上的主动力为:作用于手柄上的力偶 \left( {\mathbf{F}，{\mathbf{F}}^{\prime }}\right)，被压物体对压板的阻力 {\mathbf{F}}_{\mathrm{N}} 。

给系统以虚位移，将手柄按螺纹方向转过极小角 {\delta \varphi }，于是螺杆和压板得到向下的位移 {\delta s} 。

计算所有主动力在虚位移上所做虚功的和， 列出虚功方程， 有

\sum \delta {W}_{F} = - {F}_{\mathrm{N}} \cdot {\delta s} + {2Fl} \cdot {\delta \varphi } = 0

由机构的传动关系知: 对于单头螺纹，手柄转一周，螺杆上升或下降一个螺距 h，故有

\frac{\delta \varphi }{2\pi } = \frac{\delta s}{h}\text{，即 }{\delta s} = \frac{h}{2\pi }{\delta \varphi }

将上述虚位移 {\delta s} 与 {\delta \varphi } 的关系式代入虚功方程中，得

\sum \delta {W}_{F} = \left( {{2Fl} - \frac{{F}_{\mathrm{N}}h}{2\pi }}\right) {\delta \varphi } = 0

因 {\delta \varphi } 是任意的，故有

{2Fl} - \frac{{F}_{\mathrm{N}}h}{2\pi } = 0

解得

{F}_{\mathrm{N}} = \frac{4\pi l}{h}F

作用于被压榨物体上的力与此力等值反向。

例 3 图 9 所示椭圆规机构中，连杆 {AB} 长为 l，滑块 A\text{、}B 与杆重均不计，忽略各处摩擦，机构在图示位置平衡。求主动力 {\mathbf{F}}_{A} 与 {\mathbf{F}}_{B} 之间的关系。

解:研究整个机构，系统约束为理想约束。对此题，可用下述两种方法求解。

图 9

(1)用解析法。建立图示坐标系，由

\sum \left( {{F}_{ix}\delta {x}_{i} + {F}_{iy}\delta {y}_{i} + {F}_{ix}\delta {z}_{i}}\right) = 0

有

- {F}_{B}\delta {x}_{B} - {F}_{A}\delta {y}_{A} = 0 \tag{a}

由例 1 的式 (c)， 得

\frac{\delta {x}_{B}}{\delta {y}_{A}} = \frac{{y}_{A} - {y}_{B}}{{x}_{A} - {x}_{B}} = - \tan \varphi \tag{b}

代入式(a)，得

- \left( {{F}_{A} - {F}_{B}\tan \varphi }\right) \delta {y}_{A} = 0

由 \delta {y}_{A} 的任意性，得到

{F}_{A} = {F}_{B}\tan \varphi

(2)为求各虚位移分量应满足的数学关系式(b)，也可以采用 “虚速度法”。假想 \delta {\mathbf{r}}_{A} 、 \delta {\mathbf{r}}_{B} 是滑块 A\text{、}B 在微小时间间隔 {\delta t} 内产生的 “虚位移”，定义其对应的 “虚速度” 为

{v}_{A} = \frac{\delta {r}_{A}}{\delta t}，\;{v}_{B} = \frac{\delta {r}_{B}}{\delta t}

则有

\frac{\delta {x}_{B}}{\delta {y}_{A}} = \frac{\delta {x}_{B}/{\delta t}}{\delta {y}_{A}/{\delta t}} = \frac{{v}_{Bx}}{{v}_{Ay}} \tag{c}

由图 9， 得

{v}_{Bx} = {v}_{B}，\;{v}_{Ay} = - {v}_{A}

而由速度投影定理， 得

{v}_{A}\sin \varphi = {v}_{B}\cos \varphi

代入式 (c)，同样得到式 (b) 的结果。

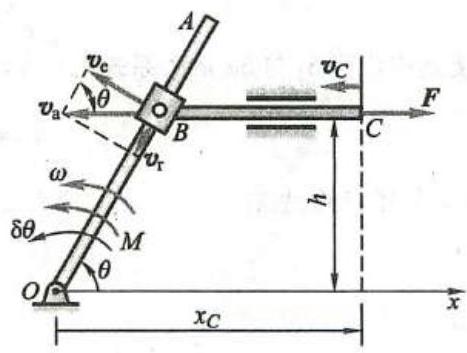
例 4 图 10 所示机构， 不计各构件自重与各处摩擦， 求机构在图示位置平衡时， 主动力偶矩 M 与主动力 \mathbf{F} 之间的关系。

解:研究整个系统，约束为理想约束。列虚功方程， 有

{M\delta \theta } + {F\delta }{x}_{c} = 0

图 10

其中， {\delta \theta } 为质点系虚位移所引起角度 \theta 的微小变化， 可看成是广义的 “虚位移”；\delta {x}_{c} 为点 C 沿 x 轴正向的虚位移分量。 {\delta \theta } 与 \delta {x}_{c} 之间的关系可采用虚速度法求得。如图 10 所示，取套筒 B 为动点，杆 {OA} 为动参考系， 则由点的速度合成公式， 得

{v}_{\mathrm{e}} = {OB} \cdot \omega = \frac{h\omega }{\sin \theta }，\;{v}_{B} = {v}_{C} = \frac{h\omega }{{\sin }^{2}\theta }

从而有

\frac{\delta {x}_{c}}{\delta \theta } = \frac{{v}_{cx}}{\omega } = - \frac{{v}_{c}}{\omega } = - \frac{h}{{\sin }^{2}\theta }

也可建立图示坐标系， 由几何关系， 得到

{x}_{c} = h\cot \theta + {BC}，\;\delta {x}_{c} = - \frac{h\delta \theta }{{\sin }^{2}\theta }

将上述虚位移分量之间的关系式代入虚功方程，由 {\delta \theta } 的任意性，得到

M = \frac{Fh}{{\sin }^{2}\theta }

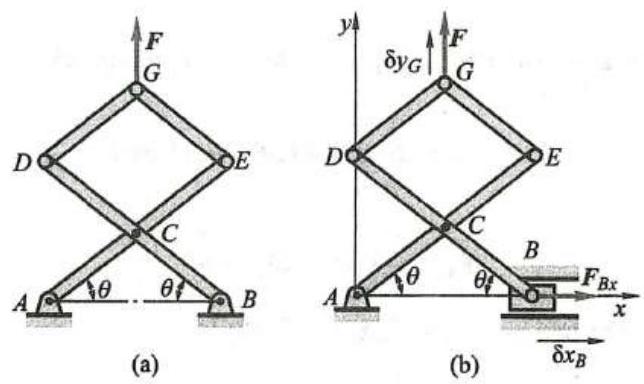
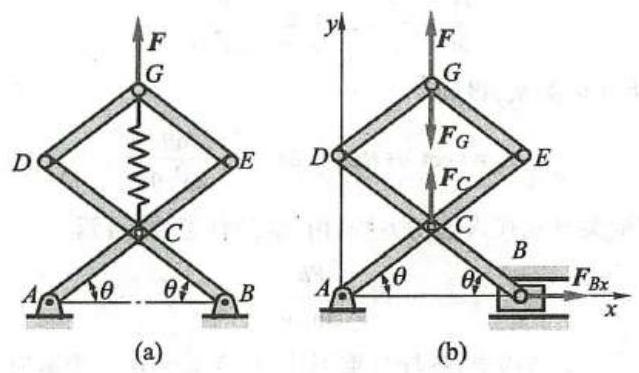
例 5 图 11a 所示结构中，各杆自重不计，在点 G 作用一铅垂向上的力 F 。已知 {AC} = {CE} = {CD} = {CB} = {DG} = {GE} = l，求支座 B 的水平约束力。

图 11

解:为求支座 B 处的水平约束力，需把 B 处水平约束解除，以力 {\mathbf{F}}_{B\mathrm{x}} 代替，将此力看作主动力，则结构变成图 11b 所示的机构。用解析法，建立坐标系如图所示，列虚功方程，有

\delta {W}_{F} = 0，\;{F}_{Bx} \cdot \delta {x}_{B} + F \cdot \delta {y}_{G} = 0

以 \theta 为参数写出点 B 的坐标 {x}_{B} 与点 G 的坐标 {y}_{G}，有

{x}_{B} = {2l}\cos \theta，\;{y}_{C} = {3l}\sin \theta

其变分为

\delta {x}_{B} = - {2l}\sin {\theta \delta \theta }，\;\delta {y}_{G} = {3l}\cos {\theta \delta \theta }

将 \delta {x}_{B} 、 \delta {y}_{G} 代入虚功方程，得

\left( {-2{F}_{Bx}\sin \theta + {3F}\cos \theta }\right) {l\delta \theta } = 0

解得

{F}_{Bx} = \frac{3}{2}F\cot \theta

此题如果在点 C\text{、}G 之间连接一自重不计、刚度系数为 k 的弹簧，如图 12a 所示。在图示位置弹簧已有伸长量 {\delta }_{0}，其他条件不变，仍求支座 B 的水平约束力。则仍需解除 B 处水平方向约束，去掉弹簧，均代之以力，如图 12b 所示。在图示位置，弹簧有伸长量 {\delta }_{0}，所以弹性力 {F}_{C} = {F}_{G} = k{\delta }_{0} 。仍用解析法，列虚功方程，有

\delta {W}_{F} = 0，\;{F}_{Bx} \cdot \delta {x}_{B} + {F}_{C} \cdot \delta {y}_{C} - {F}_{C} \cdot \delta {y}_{C} + F \cdot \delta {y}_{C} = 0

而

{x}_{B} = {2l}\cos \theta，\;{y}_{C} = l\sin \theta，\;{y}_{G} = {3l}\sin \theta

其变分为

\delta {x}_{B} = - {2l}\sin {\theta \delta \theta }，\;\delta {y}_{C} = l\cos {\theta \delta \theta }，\;\delta {y}_{C} = {3l}\cos {\theta \delta \theta }

图 12

代入虚功方程， 得

\left( {-2{F}_{Bx}\sin \theta - {2k}{\delta }_{0}\cos \theta + {3F}\cos \theta }\right) {l\delta \theta } = 0

解得

{F}_{Bx} = \frac{3}{2}F\cot \theta - k{\delta }_{0}\cot \theta

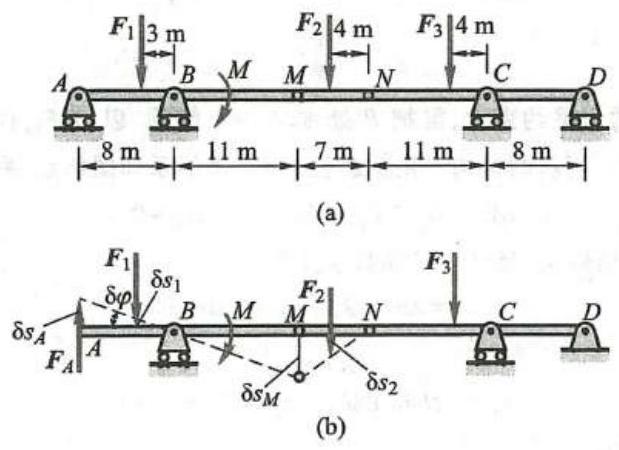
例 6 求图 13a 所示无重组合梁支座 A 的约束力。

图 13

解: 解除支座 A 的约束，代之以约束力 {\mathbf{F}}_{A}，将 {\mathbf{F}}_{A} 看作为主动力，如图 13b 所示。假想支座 A 产生如图所示虚位移，则在约束允许的条件下，各点虚位移如图所示，列虚功方程，有

\delta {W}_{p} = 0，\;{F}_{A} \cdot \delta {s}_{A} - {F}_{1} \cdot \delta {s}_{1} + M \cdot {\delta \varphi } + {F}_{2} \cdot \delta {s}_{2} = 0

从图中的几何关系可得

{\delta \varphi } = \frac{\delta {s}_{A}}{8\mathrm{\;m}}，\;\delta {s}_{1} = 3\mathrm{\;m} \cdot {\delta \varphi } = \frac{3}{8}\delta {s}_{A}，\;\delta {s}_{M} = {11}\mathrm{\;m} \cdot {\delta \varphi } = \frac{11}{8}\delta {s}_{A}

\delta {s}_{2} = \frac{4}{7}\delta {s}_{M} = \frac{4}{7} \times \frac{11}{8}\delta {s}_{A} = \frac{11}{14}\delta {s}_{A}

代入虚功方程得

{F}_{A} = \frac{3}{8}{F}_{1} - \frac{11}{14}{F}_{2} - \frac{1}{8\mathrm{\;m}}M

由以上数例可见， 用虚位移原理求解机构的平衡问题， 关键是找出各虚位移之间的关系。一般应用中，可采用下列三种方法建立各虚位移之间的关系。

(1)设机构某处产生虚位移，作图给出机构各处的虚位移，直接按几何关系， 确定各有关虚位移之间的关系，如例 2、例 6。

(2)建立坐标系，选定一合适的自变量，写出各有关点的坐标，对各坐标进行变分运算，确定各虚位移之间的关系，如例 4、例 5。

(3)按运动学方法，设某处产生虚速度，计算各有关点的虚速度。计算各虚速度时， 可采用运动学中各种方法， 如点的合成运动方法、刚体平面运动的基点法、速度投影定理、瞬心法及写出运动方程再求导数等，如例 3、例 4。

用虚位移原理求解结构的平衡问题时， 若要求某一支座约束力， 首先需解除该支座约束而代以约束力，把结构变为机构，把约束力当作主动力。这样，在虚位移方程中只包含一个未知力，然后用虚位移原理求解，如例 5、例 6。若需求多个约束力，则需要一个一个地解除约束用虚位移原理求解，这样求解有时并不方便， 如例 5、例 6， 若要求各处约束力， 则不如用平衡方程方便。