达朗贝尔原理

[Max]

达朗贝尔原理提供了研究非自由质点系动力学的一个新的普遍的方法，由达朗贝尔原理给出的求解动力学问题的静力学方法称为动静法。

1 惯性力 · 质点的达朗贝尔原理

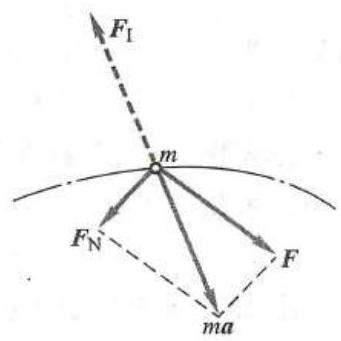
设一质点的质量为 m ，加速度为 a ，作用于质点的主动力为 F ，约束力为 {F}_{\mathrm{N}} ，如图1 所示。由牛顿第二定律，有

{ma} = \mathbf{F} + {\mathbf{F}}_{\mathrm{N}}

图1

将上式移项写为

\mathbf{F} + {\mathbf{F}}_{\mathrm{N}} - {ma} = \mathbf{0}

令

{\mathbf{F}}_{1} = - {ma} \tag{1}

有

\mathbf{F} + {\mathbf{F}}_{N} + {\mathbf{F}}_{1} = \mathbf{0} \tag{2}

{\mathbf{F}}_{1} 具有力的量纲，且与质点的惯性有关，可以把 {\mathbf{F}}_{1} 假想为一个力，称之为质点的惯性力。它的大小等于质点的质量与加速度的乘积，它的方向与质点加速度的方向相反。式 (2) 可解释为：作用在质点上的主动力、约束力和它的惯性力在形式上组成平衡力系。这就是质点的达朗贝尔原理。

应该强调指出，质点并非处于平衡状态，这样做的目的是使动力学问题可以借用静力学的理论和方法求解。对非自由质点系动力学问题，这一方法具有很多优越性，因此在工程中应用比较广泛。达朗贝尔原理与虚位移原理构成了分析力学的基础。

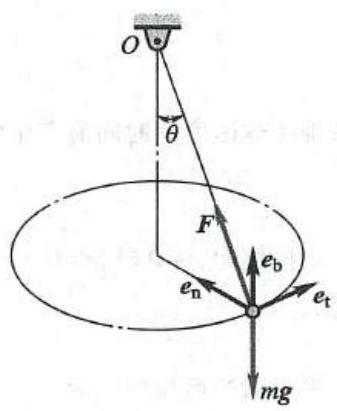
例1 用达朗贝尔原理求解：一圆锥摆，质量 m = {0.1}\mathrm{\;{kg}} 的小球系于长 l = {0.3}\mathrm{\;m} 的绳上，绳的另一端系在固定点 O ，并与铅垂线成 \theta = {60}^{ \circ } 角。如小球在水平面内做匀速圆周运动，求小球的速度 v 与绳的张力的大小。

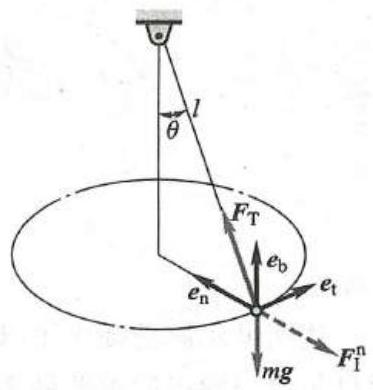
解：用达朗贝尔原理解题时，首先也要进行受力分析，而且一定要画出惯性力。视小球为质点，其受重力 (主动力) {mg} 与绳拉力 (约束力) {F}_{\mathrm{T}} 作用。质点做匀速圆周运动，只有法向加速度，因此只有法向惯性力，如图2 所示，且

{F}_{1}^{\mathrm{n}} = m{a}_{\mathrm{n}} = m\frac{{v}^{2}}{l\sin \theta }

图2

根据质点的达朗贝尔原理，这三力在形式上组成平衡力系，即

{mg} + {\mathbf{F}}_{\mathrm{T}} + {\mathbf{F}}_{1}^{\mathrm{n}} = \mathbf{0}

取上式在图示自然轴上的投影式，有

\sum {F}_{\mathrm{b}} = 0，\;{F}_{\mathrm{T}}\cos \theta - {mg} = 0

\sum {F}_{\mathrm{n}} = 0，\;{F}_{\mathrm{T}}\sin \theta - {F}_{1}^{\mathrm{n}} = 0

解得

{F}_{\mathrm{T}} = \frac{mg}{\cos \theta } = {1.96}\mathrm{\;N}，\;v = \sqrt{\frac{{F}_{\mathrm{T}}l{\sin }^{2}\theta }{m}} = {2.1}\mathrm{\;m}/\mathrm{s}

2 质点系的达朗贝尔原理

设质点系由 n 个质点组成，其中任一质点 i 的质量为 {m}_{i} ，加速度为 {\mathbf{a}}_{i} ，把作用于此质点上的所有力分为主动力的合力 {\mathbf{F}}_{i} 、约束力的合力 {\mathbf{F}}_{\mathrm{N}i} ，对这个质点假想地加上它的惯性力 {\mathbf{F}}_{1i} = - {m}_{i}{\mathbf{a}}_{i} ，由质点的达朗贝尔原理，有

{\mathbf{F}}_{i} + {\mathbf{F}}_{\mathrm{N}i} + {\mathbf{F}}_{\mathrm{I}i} = \mathbf{0}\;\left( {i = 1，2，\cdots ，n}\right) \tag{3}

上式表明，质点系中每个质点上作用的主动力、约束力和它的惯性力在形式上组成平衡力系，这是质点系的达朗贝尔原理。

把作用于第 i 个质点上的所有力分为外力的合力 {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } ，内力的合力 {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) } ，则式 (3) 可改写为

{\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } + {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) } + {\mathbf{F}}_{Ii} = \mathbf{0}\;\left( {i = 1，2，\cdots ，n}\right)

这表明，质点系中每个质点上作用的外力、内力和它的惯性力在形式上组成平衡力系。由静力学知，空间任意力系平衡的充分必要条件是力系的主矢和对于任一点的主矩等于零，即

\sum {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } + \sum {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) } + \sum {\mathbf{F}}_{\mathrm{I}i} = \mathbf{0}

\sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) }\right) + \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) }\right) + \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{\mathrm{I}i}\right) = \mathbf{0}

由于质点系的内力总是成对存在，且等值、反向、共线，因此有 \sum {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) } = \mathbf{0} 和 \sum {M}_{o}\left( {\mathbf{F}}_{i}^{\left( \mathrm{i}\right) }\right) = \mathbf{0} ，于是有

\left. \begin{array}{l} \sum {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } + \sum {\mathbf{F}}_{\mathrm{I}i} = \mathbf{0} \\ \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) }\right) + \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{\mathrm{I}i}\right) = \mathbf{0} \end{array}\right\} \tag{4}

式(4)表明，作用在质点系上的所有外力与所有质点的惯性力系在形式上组成平衡力系，这是质点系达朗贝尔原理的又一表述，也是更常用的一种表述。

在静力学中，称 \sum {\mathbf{F}}_{i} 为主矢，\sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}\right) 为对点 O 的主矩，现在称 \sum {\mathbf{F}}_{1i} 为惯性力系的主矢，\sum {M}_{0}\left( {F}_{\mathrm{{Li}}}\right) 为惯性力系对点 O 的主矩。与静力学中空间任意力系的平衡条件

{\mathbf{F}}_{\mathrm{R}} = \sum {\mathbf{F}}_{i} = \sum {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } = \mathbf{0}，\;{\mathbf{M}}_{o} = \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}\right) = \sum {\mathbf{M}}_{o}\left( {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) }\right) = \mathbf{0}

比较，式 (4) 中分别多出了惯性力系的主矢 \sum {\mathbf{F}}_{1i} 与惯性力系对点 O 的主矩 \sum {\mathbf{M}}_{O}\left( {\mathbf{F}}_{\mathrm{{Li}}}\right) ，由质点系的达朗贝尔原理，这在形式上也是一个平衡力系，因而可用静力学求解各种平衡力系的方法求解动力学问题。

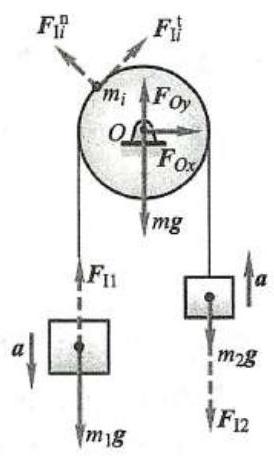
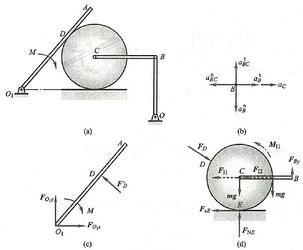
例2 如图3 所示，定滑轮的半径为 r ，绕水平轴 O 转动，质量 m 均匀分布在轮缘上。跨过定滑轮的无重绳的两端挂有质量分别为 {m}_{1} 和 {m}_{2} 的重物 \left( {{m}_{1} > {m}_{2}}\right) ，绳与轮间不打滑，轴承摩擦忽略不计，求重物的加速度。

解：取定滑轮与两重物组成的质点系为研究对象，作用于此质点系的外力有重力 {m}_{1}\mathbf{g}\text{、}{m}_{2}\mathbf{g}\text{、}m\mathbf{g} 和轴承的约束力 {\mathbf{F}}_{0x}\text{、}{\mathbf{F}}_{0y} ，对两重物加惯性力如图3 所示，大小分别为

{F}_{I1} = {m}_{1}a，\;{F}_{I2} = {m}_{2}a

图3

记定滑轮边缘上任一点 i 的质量为 {m}_{i} ，加速度有切向、法向加速度，加惯性力如图所示，大小分别为

{F}_{\mathrm{I}i}^{\mathrm{t}} = {m}_{i}{r\alpha } = {m}_{i}a，\;{F}_{\mathrm{I}i}^{\mathrm{n}} = {m}_{i}\frac{{v}^{2}}{r}

列平衡方程，有

\sum {M}_{o} = 0，\;\left( {{m}_{1}g - {F}_{I1} - {m}_{2}g - {F}_{I2}}\right) r - \sum {F}_{Ii}^{t} \cdot r = 0

即

\left( {{m}_{1}g - {m}_{1}a - {m}_{2}g - {m}_{2}a}\right) r - \sum {m}_{i}{ar} = 0

注意到

\sum {m}_{i}{ar} = \left( {\sum {m}_{i}}\right) {ar} = \operatorname{mar}

解得

a = \frac{{m}_{1} - {m}_{2}}{{m}_{1} + {m}_{2} + m}g

例3 如图4a 所示均质的四分之一圆环绕水平轴以匀角速度 \omega 转动。已知：圆环半径为 r ，质量为 m ，轴承 A\text{、}B 的间距为 l ，轴 {AB} 质量忽略不计。试求图示瞬时轴承 A 的约束力。

图4

解：分析整体，所受的力包括轴承 A 和 B 的约束力，如图4b 所示。对于 \frac{1}{4} 圆环，取微小弧段虚加惯性力，有

\mathrm{d}{F}_{I} = {a}_{\mathrm{n}}\mathrm{d}m = {\omega }^{2}r\sin \theta \frac{2m}{\pi }\mathrm{d}\theta

方向如图4b 所示。

由质点系达朗贝尔原理，列平衡方程有

\sum {M}_{B} = 0，\;{\int }_{0}^{\frac{\pi }{2}}\frac{2m}{\pi }{\omega }^{2}r\sin \theta \cdot r\cos \theta \mathrm{d}\theta + {mgr}\sin {45}^{ \circ } - {F}_{A}l = 0

解得

{F}_{A} = \frac{\sqrt{2}}{2l}{mgr} + \frac{m{r}^{2}{\omega }^{2}}{\pi l}

由结果可知轴承 A 处约束力包括两部分：一部分为 {F}_{A}^{\prime } = \frac{\sqrt{2}}{2l}{mgr} ，是由重力引起的，为静约束力; 另一部分为 {F}_{A}^{\prime \prime } = \frac{m{r}^{2}{\omega }^{2}}{\pi l} ，是由惯性力引起的，为附加动约束力。附加动约束力取决于惯性力，如果只求附加动约束力，列方程时可以不考虑惯性力以外的其他力。

3 刚体惯性力系的简化

质点系内每个质点都虚加惯性力后，这些惯性力形成了一个力系，称之为惯性力系，刚体惯性力系的简化是在应用达朗贝尔原理解题时常遇到的问题。在静力学中已经讨论过力系的简化，这一简化过程是基于刚体中力系的等效原理进行的，因此，静力学中关于力系简化的内容也适用于刚体惯性力系的简化。

刚体惯性力系向任一点简化，一般得到一个力和一个力偶。力的大小和方向等于惯性力系的主矢，作用点在简化中心。力偶的力偶矩矢等于所有惯性力对简化中心的主矩。

以 {\mathbf{F}}_{\mathrm{{IR}}} 表示惯性力系的主矢，由式 (4) 中第一式与质心运动定理，有

{\mathbf{F}}_{\mathrm{{IR}}} = - \sum {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) } = - m{\mathbf{a}}_{c} \tag{5}

主矢与简化中心无关，因此刚体无论做什么运动，也无论向刚体上哪一点简化，惯性力系的主矢都由式 (5) 确定。

以 {\mathbf{M}}_{I0} 表示惯性力系的主矩，由式 (4) 中第二式，有

{\mathbf{M}}_{IO} = - \sum {\mathbf{M}}_{O}\left( {\mathbf{F}}_{i}^{\left( \mathrm{e}\right) }\right) \tag{6}

主矩一般情况下与简化中心有关。特别地，当点 O 是定点或质心时，利用对定点或质心的动量矩定理，由式 (6)，有

{\mathbf{M}}_{Io} = - \frac{\mathrm{d}{\mathbf{L}}_{o}}{\mathrm{\;d}t}\text{ 或 }{\mathbf{M}}_{Ic} = - \frac{\mathrm{d}{L}_{c}}{\mathrm{\;d}t} \tag{7}

由于此式应用时很方便，因此，在进行惯性力系简化时，经常是向定点或质心简化，这样就可以应用式(7)来求惯性力系的主矩。

下面讨论刚体平移、定轴转动和平面运动时惯性力系的简化。由于刚体无论做何种运动，也无论向哪一点简化，惯性力系的主矢都由式 (5) 确定，因此，我们仅讨论这几种情况下惯性力系的主矩。

3.1 刚体平移

刚体平移时，由前面所学内容知，平移刚体对任意点的动量矩为

{\mathbf{L}}_{0} = {\mathbf{r}}_{c} \times m{\mathbf{v}}_{c}

而对质心的动量矩为 {L}_{c} = 0 ，所以刚体平移时选质心为简化中心，由式 (7)，有

{M}_{IC} = 0 \tag{8}

因此，刚体平移时，惯性力系对任意点的主矩一般不为零。若选质心为简化中心，其主矩为零，简化为一合力。

由此有结论：平移刚体的惯性力系可以简化为通过质心的合力，其大小等于刚体的质量与加速度的乘积，合力的方向与加速度方向相反。

3.2 刚体定轴转动

刚体定轴转动时，设刚体的角速度为 \omega ，角加速度为 \alpha ，刚体内任一质点的质量为 {m}_{i} ，到转轴的距离为 {r}_{i} ，则刚体内任一质点的惯性力为 {\mathbf{F}}_{Ii} = - {m}_{i}{\mathbf{a}}_{i} 。为简单起见，在转轴上任选一点 O 为简化中心。力对点的矩矢在通过该点的某轴上的投影，等于力对该轴的矩。因此，建立直角坐标系如图5 所示，质点的坐标为 {x}_{i} 、 {y}_{i} 、 {z}_{i} 。现在分别计算惯性力系对 x 、 y 、 z 轴的矩，分别以 {M}_{Ix} 、 {M}_{Iy} 、 {M}_{Iz} 表示。

图5

质点的惯性力 {\mathbf{F}}_{Ii} = - {m}_{i}{\mathbf{a}}_{i} 可分解为切向惯性力 {\mathbf{F}}_{Ii}^{1} 与法向惯性力 {\mathbf{F}}_{Ii}^{\mathrm{n}} ，方向如图5 所示，大小分别为

{F}_{Ii}^{\mathrm{t}} = {m}_{i}{a}_{i}^{\mathrm{t}} = {m}_{i}{r}_{i}\alpha ，\;{F}_{Ii}^{\mathrm{n}} = {m}_{i}{a}_{i}^{\mathrm{n}} = {m}_{i}{r}_{i}{\omega }^{2}

惯性力系对 x 轴的矩为

{M}_{Ix} = \sum {M}_{x}\left( {\mathbf{F}}_{Ii}\right) = \sum {M}_{x}\left( {\mathbf{F}}_{Ii}^{\mathrm{t}}\right) + \sum {M}_{x}\left( {\mathbf{F}}_{Ii}^{\mathrm{n}}\right)

= \sum {m}_{i}{r}_{i}\alpha \cos {\theta }_{i} \cdot {z}_{i} + \sum - {m}_{i}{r}_{i}{\omega }^{2}\sin {\theta }_{i} \cdot {z}_{i}

因

\cos {\theta }_{i} = \frac{{x}_{i}}{{r}_{i}}，\;\sin {\theta }_{i} = \frac{{y}_{i}}{{r}_{i}}

故

{M}_{Ix} = \alpha \sum {m}_{i}{x}_{i}{z}_{i} - {\omega }^{2}\sum {m}_{i}{y}_{i}{z}_{i}

记

{J}_{xz} = \sum {m}_{i}{x}_{i}{z}_{i}，\;{J}_{yz} = \sum {m}_{i}{y}_{i}{z}_{i} \tag{9}

称之为对于 z 轴的惯性积，它取决于刚体质量对于坐标轴的分布情况。于是，惯性力系对于 x 轴的矩为

{M}_{Ix} = {J}_{xz}\alpha - {J}_{yz}{\omega }^{2} \tag{10}

同理可得惯性力系对于 y 轴的矩为

{M}_{Iy} = {J}_{yz}\alpha + {J}_{xz}{\omega }^{2} \tag{11}

惯性力系对于 z 轴的矩为

{M}_{\mathrm{I}z} = \sum {M}_{z}\left( {\mathbf{F}}_{\mathrm{I}i}^{\mathrm{t}}\right) + \sum {M}_{z}\left( {\mathbf{F}}_{\mathrm{I}i}^{\mathrm{n}}\right)

由于各质点的法向惯性力均通过 z 轴，\sum {M}_{z}\left( {\mathbf{F}}_{1i}^{\mathrm{n}}\right) = 0 ，有

{M}_{Iz} = \sum {M}_{z}\left( {F}_{Ii}^{1}\right) = \sum \left( {-{m}_{i}{r}_{i}\alpha \cdot {r}_{i}}\right) = - \left( {\sum {m}_{i}{r}_{i}^{2}}\right) \alpha = - {J}_{z}\alpha \tag{12}

综上可得，刚体定轴转动时，惯性力系向转轴上一点 O 简化的主矩为

{\mathbf{M}}_{\mathrm{I}O} = {M}_{\mathrm{I}x}\mathbf{i} + {M}_{\mathrm{I}y}\mathbf{j} + {M}_{\mathrm{I}z}\mathbf{k}

= \left( {{J}_{xz}\alpha - {J}_{yz}{\omega }^{2}}\right) \mathbf{i} + \left( {{J}_{yz}\alpha + {J}_{xz}{\omega }^{2}}\right) \mathbf{j} - {J}_{z}\alpha \mathbf{k} \tag{13}

如果刚体有质量对称平面且该平面与转轴 z 垂直，简化中心 O 取为此平面与转轴 z 的交点，则

{J}_{xz} = \sum {m}_{i}{x}_{i}{z}_{i} = 0，\;{J}_{yz} = \sum {m}_{i}{y}_{i}{z}_{i} = 0

则惯性力系简化的主矩为

{M}_{IO} = {M}_{Iz} = - {J}_{z}\alpha

工程中绕定轴转动的刚体常常有质量对称平面。

结论：当刚体有质量对称平面且绕垂直于此对称平面的轴做定轴转动时，惯性力系向转轴与对称平面交点简化时，得位于此平面内的一个力和一个力偶。这个力等于刚体质量与质心加速度的乘积，方向与质心加速度方向相反，作用线通过转轴；这个力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘积，转向与角加速度相反。

3.3 刚体平面运动 (平行于质量对称平面)

工程中，做平面运动的刚体常常有质量对称平面，且平行于此平面运动，现仅限于讨论这种情况下惯性力系的简化。刚体做平面运动，其上各质点的惯性力组成的空间力系，可简化为在质量对称平面内的平面力系。取质量对称平面内的平面图形如图6 所示。由运动学知，平面图形的运动可分解为随基点的平移与绕基点的转动。现取质心 C 为基点，设质心的加速度为 {a}_{c} ，绕质心转动的角速度为 \omega ，角加速度为 \alpha ，与刚体绕定轴转动相似，此时惯性力系向质心 C 简化的主矩为

{M}_{IC} = - {J}_{C}\alpha \tag{14}

式中，{J}_{c} 为刚体对通过质心且垂直于质量对称平面的轴的转动惯量。

结论：有质量对称平面的刚体，平行于此平面运动时，刚体的惯性力系简化为在此平面内的一个力和一个力偶。这个力通过质心，其大小等于刚体的质量与质心加速度的乘积，其方向与质心加速度的方向相反；这个力偶的力偶矩等于刚体对过质心且垂直于质量对称平面的轴的转动惯量与角加速度的乘积，转向与角加速度相反。

图6

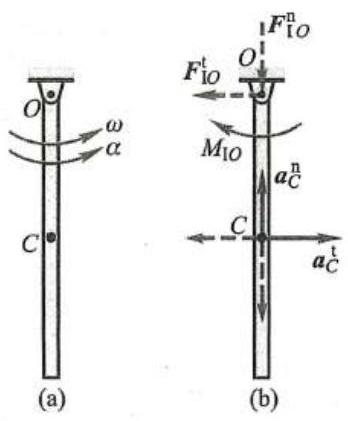
例4 如图7a 所示均质杆的质量为 m ，长为 l ，绕定轴 O 转动的角速度为 \omega ，角加速度为 \alpha 。求惯性力系向点 O 简化的结果 (方向在图上画出)。

图7

解：该杆做定轴转动，惯性力系向点 O 简化的主矢、主矩大小为

{F}_{Io}^{1} = m \cdot \frac{l}{2}\alpha ，\;{F}_{Io}^{n} = m \cdot \frac{l}{2}{\omega }^{2}，\;{M}_{Io} = \frac{1}{3}m{l}^{2} \cdot \alpha

方向分别如图7b 所示。

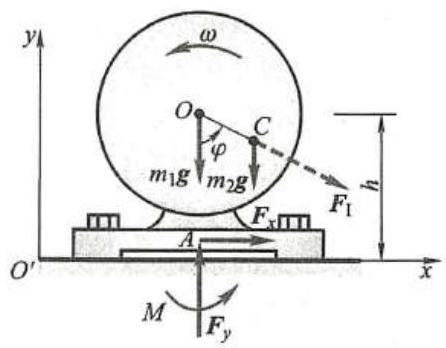
例5 如图8 所示，电动机定子及其外壳总质量为 {m}_{1} ，质心位于 O 处。转子的质量为 {m}_{2} ，质心位于点 C 处，偏心距 {OC} = e ，图示平面为转子的质量对称平面。电动机用地脚螺栓固定于水平基础上，转轴 O 与水平基础间的距离为 h 。运动开始时，转子质心 C 位于最低位置，转子以匀角速度 \omega 转动。求基础与地脚螺栓给电动机的约束力。

解：取电动机整体为研究对象，作用于其上的外力有重力 {m}_{1}\mathbf{g} 与 {m}_{2}\mathbf{g} ，基础与地脚螺栓给电动机的约束力向点 A 简化，得一力偶 M 与一力 F ，力 F 以其分力 {F}_{x}\text{、}{F}_{y} 表示。定子与外壳无需加惯性力，对转子来说，由于角加速度 \alpha = 0 ，无需加惯性力矩，而质心加速度为 e{\omega }^{2} ，因此只需加惯性力 {\mathbf{F}}_{I} ，如图8 所示，其大小为

{F}_{I} = {m}_{2}e{\omega }^{2}

图8

根据质点系达朗贝尔原理，此电动机上的外力与惯性力形成一个平衡力系，列平衡方程，有

\sum {F}_{x} = 0，\;{F}_{x} + {F}_{I}\sin \varphi = 0

\sum {F}_{y} = 0，\;{F}_{y} - \left( {{m}_{1} + {m}_{2}}\right) g - {F}_{I}\cos \varphi = 0

\sum {M}_{A} = 0，\;M - {m}_{2}{ge}\sin \varphi - {F}_{I}h\sin \varphi = 0

因 \varphi = {\omega t} ，解上述方程，得

{F}_{x} = - {m}_{2}e{\omega }^{2}\sin {\omega t}，\;{F}_{y} = \left( {{m}_{1} + {m}_{2}}\right) g + {m}_{2}e{\omega }^{2}\cos {\omega t}

M = {m}_{2}{ge}\sin {\omega t} + {m}_{2}e{\omega }^{2}h\sin {\omega t}

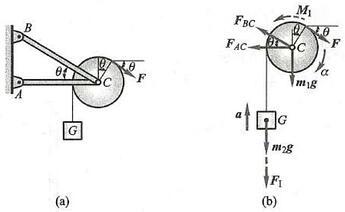
例6 图示均质定滑轮 C 铰接在无重支架 {ABC} 上。已知：定滑轮 C 质量为 {m}_{1} ，重物 G 的质量为 {m}_{2} ，夹角 \theta = {30}^{ \circ } ，绳与轮间无相对滑动。试求用已知力 F 拉起重物 G 时，(1) 重物 G 上升的加速度; (2) 杆 {AC} 与 {BC} 所受的力。

解：取整个系统为研究对象，如图9b 所示，受力包括定滑轮 C 的重力 {m}_{1}g 、重物 G 的重力 {m}_{2}g 、杆 {AC} 的力 {F}_{AC} 、杆 {BC} 的力 {F}_{BC} ，以及力 F 。重物 G 做平移，如图9b 所示虚加惯性力，大小为

{F}_{1} = {m}_{2}a

图9

定滑轮 C 做定轴转动，质心加速度为零，因此惯性力系的简化结果只有一力偶，如图9b 所示，大小为

{M}_{I} = \frac{1}{2}{m}_{1}{r}^{2}\alpha = \frac{1}{2}{m}_{1}{r}^{2}\frac{a}{r} = \frac{1}{2}{m}_{1}{ra}

由质点系达朗贝尔原理，列平衡方程有

\sum {M}_{C} = 0，\left( {{m}_{2}g + {F}_{1}}\right) r - {Fr} + {M}_{I} = 0

\sum {F}_{x} = 0，F\cos \theta - {F}_{BC}\cos \theta - {F}_{AC} = 0

\sum {F}_{y} = 0，{F}_{BC}\sin \theta - F\sin \theta - \left( {{m}_{1} + {m}_{2}}\right) g - {F}_{I} = 0

解得

a = \frac{2\left( {F - {m}_{2}g}\right) }{{m}_{1} + 2{m}_{2}}

{F}_{BC} = \frac{\left( {{m}_{1} + 6{m}_{2}}\right) F + 2{m}_{1}\left( {{m}_{1} + 3{m}_{2}}\right) g}{{m}_{1} + 2{m}_{2}}

{F}_{AC} = - \frac{\sqrt{3}\left\lbrack {2{m}_{2}F + {m}_{1}\left( {{m}_{1} + 3{m}_{2}}\right) g}\right\rbrack }{{m}_{1} + 2{m}_{2}}

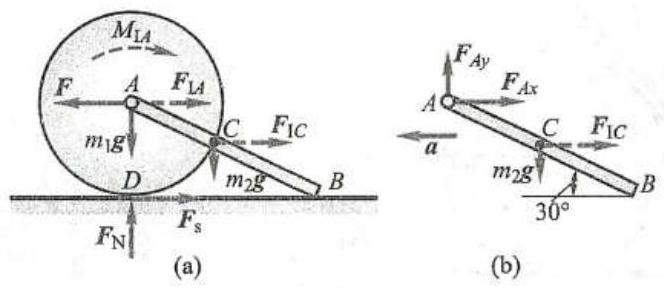
例7 均质圆盘质量为 {m}_{1} ，半径为 R 。均质杆 {AB} 长 l = {2R} ，质量为 {m}_{2} 。杆端 A 与圆盘中心为光滑铰接，如图10a 所示。如在 A 处加一水平拉力 \mathbf{F} ，使圆盘沿水平面纯滚动。力 \mathbf{F} 为多大方能使杆的 B 端刚好离开地面? 为保证纯滚动，圆盘与地面间的静摩擦因数应为多大?

解：杆刚好离开地面时仍为平移，则地面约束力为零，设其加速度为 a ，取杆为研究对象，杆所受的力并加上惯性力如图10b 所示，其中 {F}_{IC} = {m}_{2}a 。按达朗贝尔原理列平衡方程，有

\sum {M}_{A} = 0，\;{m}_{2}{aR}\sin {30}^{ \circ } - {m}_{2}{gR}\cos {30}^{ \circ } = 0

解出

a = \sqrt{3}g

图10

取整体为研究对象，所受的力并加上惯性力如图10a 所示，其中

{F}_{\mathrm{{Ii}}} = {m}_{1}a，\;{M}_{\mathrm{{Ii}}} = \frac{1}{2}{m}_{1}{R}^{2}\frac{a}{R}

由

\sum {M}_{D} = 0，\;{FR} - {F}_{IA}R - {M}_{IA} - {F}_{IC}R\sin {30}^{ \circ } - {m}_{2}{gR}\cos {30}^{ \circ } = 0

解得

F = \left( {\frac{3}{2}{m}_{1} + {m}_{2}}\right) \sqrt{3}g

由

\sum {F}_{x} = 0，\;F - {F}_{\mathrm{s}} - \left( {{m}_{1} + {m}_{2}}\right) a = 0

解出

{F}_{\mathrm{s}} = \frac{\sqrt{3}}{2}{m}_{1}g

而

{F}_{\mathrm{s}} \leq {f}_{\mathrm{s}}{F}_{\mathrm{N}} = {f}_{\mathrm{s}}\left( {{m}_{1} + {m}_{2}}\right) g

解得

{f}_{\mathrm{s}} \geq \frac{{F}_{\mathrm{s}}}{{F}_{\mathrm{N}}} = \frac{\sqrt{3}{m}_{1}}{2\left( {{m}_{1} + {m}_{2}}\right) }

例8 试利用达朗贝尔原理求解：圆盘 C 为均质圆盘，质量为 m ，半径为 R ，可沿水平面纯滚动。杆 {BC} 为均质杆，质量为 m ，处于水平位置。杆 {OB} 质量忽略不计，处于铅垂位置，且有 {BC} = {OB} = {2R} 。杆 {O}_{1}A 质量忽略不计，保持与圆盘 C 光滑接触。 最初系统处于静止状态， \varphi = {60}^{ \circ } 。现在给杆 {O}_{1}A 施加一顺时针转向，力偶矩为 M 的力偶。试求施加力偶瞬时杆 {O}_{1}A 、杆 {BC} 、杆 {OB} 、圆盘 C 的角加速度 \alpha 、 {\alpha }_{BC} 、 {\alpha }_{OB} 、 {\alpha }_{C} 及圆盘和水平面接触点 E 处的摩擦力大小。

解：平面机构如图11a 所示。初始瞬时，各构件的角速度均为零。依据结论可得圆盘质心 C 的加速度 {a}_{c} 与点 B 的加速度 {a}_{B} 及杆 {O}_{1}A 的角加速度 \alpha ，杆 {OB} 的角加速度 {\alpha }_{OB} 与杆 {O}_{1}A 的角加速度 \alpha ，以及圆盘 C 的角加速度 {\alpha }_{C} 与杆 {O}_{1}A 的角加速度 \alpha 分别存在如下关系：

{a}_{C} = {a}_{B} = {2\alpha R}，\;{\alpha }_{OB} = \alpha ，\;{\alpha }_{C} = {2\alpha }

参看图11b，沿 {a}_{B}^{n} 方向投影有 {a}_{B}^{n} = - {a}_{BC}^{1} = - {\alpha }_{BC} \cdot {BC} = 0 ，则得

{\alpha }_{BC} = 0

可知杆 {BC} 的角速度和角加速度均为零，则其质心的加速度为 a = {a}_{C} = {2\alpha R} 。

分析杆 {O}_{1}A ，受力图如图11c 所示，由于该杆的质量不计，可列平衡方程为

\sum {M}_{{o}_{i}} = 0，\;M - {F}_{D}^{\prime } \cdot \sqrt{3}R = 0

图11

解得

{F}_{D}^{\prime } = \frac{M}{\sqrt{3}R}

分析圆盘 C 和杆 {BC} ，受力图如图11d 所示。其中圆盘 C 虚加惯性力 {F}_{11} 和 {M}_{11} ，杆 {BC} 虚加惯性力 {F}_{12} ，大小分别为

{F}_{I1} = {F}_{I2} = m{a}_{c} = {2m\alpha R}，\;{M}_{I1} = \frac{1}{2}m{R}^{2}{\alpha }_{c} = {m\alpha }{R}^{2}

依据达朗贝尔原理列平衡方程有

\sum {F}_{x} = 0，\;{F}_{D}\cos {30}^{ \circ } - {F}_{I1} - {F}_{I2} - {F}_{sE} = 0

\sum {M}_{E}(F) = 0，\;{M}_{I1} - {F}_{D}R\sin {60}^{ \circ } + \left( {{F}_{I1} + {F}_{I2}}\right) R = 0

解得

{\alpha }_{0_{1}A} = \alpha = \frac{M}{{10m}{R}^{2}}，\;{\alpha }_{c} = {2\alpha } = \frac{M}{{5m}{R}^{2}}

{\alpha }_{BC} = 0，\;{\alpha }_{OB} = \alpha = \frac{M}{{10m}{R}^{2}}，\;{F}_{sE} = \frac{M}{10R}

由以上例题可见，用动静法求解动力学问题的步骤与求解静力学平衡问题的步骤相似，只是在分析物体受力时，应加上相应的惯性力; 对于刚体，则应按其运动形式的不同，加上相应惯性力系的简化结果。

为计算方便，加惯性力时，主矢与主矩的方向在图上应与加速度 \mathbf{a} 及角加速度 \mathbf{\alpha } 反向，而列出的惯性力的表达式只表示大小，在实际计算时，按图示方向考虑正负即可，而不用再加负号了。

4 绕定轴转动刚体的轴承附加动约束力

在日常生活和工程实际中，有大量绕定轴转动的刚体 (电动机、柴油机、电风扇、车床主轴等)，如何使这些机械在转动时不产生破坏、振动与噪声，是工程师非常关心的问题。如果这些机械在转动起来之后轴承受力与不转时轴承受力一样，则一般说来这些机械不会产生破坏，也不会产生振动与噪声。由前面已知静约束力与动约束力的概念，对绕定轴转动的刚体，如果能够消除轴承附加动约束力，使轴承只受到静约束力作用，就可以做到这一点。为此，先把任意一个绕定轴转动刚体的轴承全约束力(包括静约束力与附加动约束力)求出来，然后再推出消除附加动约束力的条件。

图12

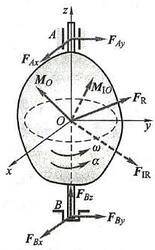
设任一刚体绕轴 {AB} 定轴转动，角速度为 \omega ，角加速度为 \alpha 。取此刚体为研究对象，转轴上一点 O 为简化中心。其上所有的主动力向点 O 简化的主矢与主矩分别以 {\mathbf{F}}_{\mathrm{R}} 与 {\mathbf{M}}_{O} 表示，惯性力系向点 O 简化的主矢与主矩分别以 {\mathbf{F}}_{\mathrm{{IR}}} 与 {\mathbf{M}}_{\mathrm{I}O} 表示 (注意 {\mathbf{F}}_{\mathrm{{IR}}} 没有沿 z 轴方向的分量)，轴承 A\text{、}B 处的 5 个全约束力分别以 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay}\text{、}{\mathbf{F}}_{Bx} 、 {\mathbf{F}}_{By}\text{、}{\mathbf{F}}_{Bz} 表示，如图12 所示。

为求出轴承 A\text{、}B 处的全约束力，建立坐标系如图12 所示。根据质点系的达朗贝尔原理，列平衡方程如下：

\sum {F}_{x} = 0，\;{F}_{Ax} + {F}_{Bx} + {F}_{\mathrm{R}x} + {F}_{\mathrm{{IR}}x} = 0

\sum {F}_{y} = 0，\;{F}_{Ay} + {F}_{By} + {F}_{\mathrm{R}y} + {F}_{\mathrm{{IR}}y} = 0

\sum {F}_{z} = 0，\;{F}_{Bz} + {F}_{\mathrm{R}z} = 0

\sum {M}_{x} = 0，\;{F}_{By} \cdot {OB} - {F}_{Ay} \cdot {OA} + {M}_{x} + {M}_{Ix} = 0

\sum {M}_{y} = 0，\;{F}_{Ax} \cdot {OA} - {F}_{Bx} \cdot {OB} + {M}_{y} + {M}_{Iy} = 0

由上述 5 个方程解得轴承全约束力为

\left. \begin{array}{l} {F}_{Ax} = - \frac{1}{AB}\left\lbrack {\left( {{M}_{y} + {F}_{\mathrm{R}s} \cdot {OB}}\right) + \left( {{M}_{Iy} + {F}_{\mathrm{{IR}}s} \cdot {OB}}\right) }\right\rbrack \\ {F}_{Ay} = \frac{1}{AB}\left\lbrack {\left( {{M}_{x} - {F}_{\mathrm{R}y} \cdot {OB}}\right) + \left( {{M}_{Ix} - {F}_{\mathrm{{IR}}y} \cdot {OB}}\right) }\right\rbrack \\ {F}_{Bs} = \frac{1}{AB}\left\lbrack {\left( {{M}_{y} - {F}_{\mathrm{R}x} \cdot {OA}}\right) + \left( {{M}_{Iy} - {F}_{\mathrm{{IR}}x} \cdot {OA}}\right) }\right\rbrack \\ {F}_{By} = - \frac{1}{AB}\left\lbrack {\left( {{M}_{x} + {F}_{\mathrm{R}y} \cdot {OA}}\right) + \left( {{M}_{Ix} + {F}_{\mathrm{{IR}}y} \cdot {OA}}\right) }\right\rbrack \\ {F}_{Ay} = - {F}_{Ay} \end{array}\right\} \tag{15}

由于惯性力没有沿 z 轴方向的分量，因此止推轴承 B 沿 z 轴的约束力 {\mathbf{F}}_{Bz} 与惯性力无关。而与 z 轴垂直的轴承约束力 {\mathbf{F}}_{Ax}\text{、}{\mathbf{F}}_{Ay}\text{、}{\mathbf{F}}_{Bx}\text{、}{\mathbf{F}}_{By} 显然与惯性力系的主矢 {\mathbf{F}}_{\mathrm{{IR}}} 与主矩 {\mathbf{M}}_{Io} 有关。由 {\mathbf{F}}_{\mathrm{{IR}}} 、 {\mathbf{M}}_{1o} 引起的轴承的约束力称为附加动约束力，要使附加动约束力等于零，必须有

{F}_{\mathrm{{IR}}x} = {F}_{\mathrm{{IR}}y} = 0，\;{M}_{\mathrm{I}x} = {M}_{Iy} = 0

即要使轴承的附加动约束力等于零的条件是：惯性力系的主矢等于零，惯性力系对于 x 轴和 y 轴的主矩等于零。

由式 (5)、式 (10) 和式 (11) ，应有

{F}_{\mathrm{{IR}}x} = - m{a}_{Cx} = 0，\;{F}_{\mathrm{{IR}}y} = - m{a}_{Cy} = 0

{M}_{Ix} = {J}_{xz}\alpha - {J}_{yz}{\omega }^{2} = 0，\;{M}_{Iy} = {J}_{yz}\alpha + {J}_{xz}{\omega }^{2} = 0

由此可见，要使惯性力系的主矢等于零，必须有 {\mathbf{a}}_{c} = \mathbf{0} ，即转轴必须通过质心。而要使 {M}_{Ix} = 0，{M}_{Iy} = 0 ，必须有 {J}_{xz} = {J}_{yz} = 0 ，即刚体对于转轴 z 的惯性积必须等于零。

于是得结论，刚体绕定轴转动时，避免出现轴承附加动约束力的条件是：转轴通过质心，刚体对转轴的惯性积等于零。

如果刚体对于通过某点的 z 轴的惯性积 {J}_{xz} 和 {J}_{yz} 等于零，则称此轴为过该点的惯性主轴。通过质心的惯性主轴，称为中心惯性主轴。所以上述结论也可叙述为：避免出现轴承附加动约束力的条件是：刚体的转轴应是刚体的中心惯性主轴。

设刚体的转轴通过质心，且刚体除重力外，没有受到其他主动力作用，则刚体可以在任意位置静止不动，称这种现象为静平衡。当刚体的转轴通过质心且为惯性主轴时，刚体转动时不出现轴承附加动约束力，称这种现象为动平衡。能够静平衡的定轴转动刚体不一定能够实现动平衡，但动平衡的定轴转动刚体肯定能够实现静平衡。

事实上，由于材料的不均匀或制造、安装误差等原因，都可能使定轴转动刚体的转轴偏离中心惯性主轴。为了避免出现轴承附加动约束力，确保机器运行安全可靠，在有条件的地方，可在专门的静平衡与动平衡试验机上进行静、动平衡试验，根据试验数据，在刚体的适当位置附加一些质量或去掉一些质量，使其达到静、动平衡。静平衡试验机可以调整质心在转轴上或尽可能地在转轴上，动平衡试验机可以调整对转轴的惯性积，使其对转轴的惯性积为零或尽可能地为零。

当然，在工程中也有相反的实例，即制造定轴转动刚体时，故意制造出偏心距，如某些打夯机，正是利用偏心块的运动来夯实地基的。

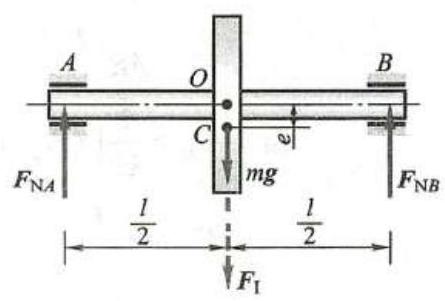
例9 如图13 所示，轮盘 (连同转轴) 的质量 m = {20}\mathrm{{kg}} ，转轴 {AB} 与轮盘的质量对称面垂直，但轮盘的质心 C 不在转轴上，偏心距 e = {0.1}\mathrm{\;{mm}} 。当轮盘以匀转速 n = {12000}\mathrm{r}/\mathrm{{min}} 转动时，求轴承 A\text{、}B 的约束力。

图13

解：由于转轴 {AB} 与轮盘的质量对称面垂直，因此转轴 {AB} 为惯性主轴，即对此轴的惯性积为零; 又由于轮盘是匀速转动，\alpha = 0 ，因此惯性力矩均为零。取此刚体为研究对象，当重心 C 位于最下端时，轴承处约束力最大，受力图如图13 所示。轮盘为匀速转动，质心 C 只有法向加速度，即

{a}_{\mathrm{n}} = e{\omega }^{2} = \frac{0.1}{1000}\mathrm{\;m} \times {\left( \frac{12000\pi }{{30}\mathrm{\;s}}\right) }^{2} = {158}\mathrm{\;m}/{\mathrm{s}}^{2}

因此惯性力大小为

{F}_{I}^{\mathrm{n}} = m{a}_{\mathrm{n}} = {3160}\mathrm{\;N}

方向如图13 所示。

由质点系的达朗贝尔原理，列平衡方程可得

{F}_{\mathrm{N}A} = {F}_{\mathrm{N}B} = \frac{1}{2}\left( {{mg} + {F}_{I}^{\mathrm{n}}}\right) = \frac{1}{2} \times \left( {{20} \times {9.8} + {3160}}\right) \mathrm{N} = {1678}\mathrm{\;N}

其中轴承附加动约束力为 \frac{1}{2}{F}_{I}^{n} = {1580}\mathrm{\;N} 。由此可见，在高速转动下，{0.1}\mathrm{\;{mm}} 的偏心距所引起的轴承附加动约束力，可达静约束力 \left( {\frac{1}{2}{mg} = {98}\mathrm{\;N}}\right) 的 16 倍之多! 而且转速越高，偏心距越大，轴承附加动约束力越大，这势必会加快轴承磨损，甚至引起轴承的破坏。

注意到惯性力 {\mathbf{F}}_{I}^{\mathrm{n}} 的方向随刚体的旋转而发生周期性的变化，使轴承附加动约束力的大小与方向也发生周期性的变化，因而势必引起机器的振动与噪声，同样会加速轴承的磨损与破坏。因此，必须尽量减小与消除偏心距。

对此题，设系统质心位于转轴上，由于安装误差，轮盘盘面与转轴成角 \theta = {1}^{ \circ } (此时转轴不是中心惯性主轴)，轮盘为均质圆盘，半径为 {200}\mathrm{\;{mm}} ，厚度为 {20}\mathrm{\;{mm}}，l = 1\mathrm{\;m} ，轮盘质量与转速不变。 可求得此时静约束力仍为 {98}\mathrm{\;N} ，但附加动约束力为 {5493}\mathrm{\;N} (计算略)，是静约束力的 56 倍之多，这对轴承受力是相当不利的，所以应尽量减小安装误差。